| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2007-11-14 5:51 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
実効値 教科書には正弦波交流の実効値の公式が出てくる
定義としては同一の抵抗RLに振幅Emの交流を印可した時の平均消費電力Pと同じ電力を消費する直流電圧Eを交流の実効値とする 直流の場合は電流と電圧が常に変わらないので消費する電力は時間によらず一定である。 それに対して交流の場合には時間とともに電流と電圧が変化するため平均を取る必要がある。Maximaで計算してみる (%i11) integrate((Em^2*sin(x)^2)/RL, x, 0, 2*%pi)/(2*%pi); (%o11) Em^2/(2*RL) これが実効電圧の直流を同じ抵抗に印可した時の電力と等しいことから P=E^2/RL=Em^2/(2*RL) 従って E=Em/sqrt(2) として公式が導かれる。 検索するとMaximaを使わなくても机上で同じ結果が得られる方法も説明されているのがみつかる、Maximでも同じことができる (%o6) (Em^2*sin(x)^2)/RL これは三角関数の公式 cos(2x)=1-2*sin(x)^2 より (%i7) trigreduce(%); (%o7) Em^2/(2*RL)-(Em^2*cos(2*x))/(2*RL) これを0から2πの区間で積分すると最初の項は定数なので区間との積となり、最後のcosの項は正と負とで相殺されて0になる。 これをEm=10,RL=10としてMaximaでグラフとして描いてみると (%i14) wxplot2d([5-5*cos(2*x)], [x,0,2*%pi])$ 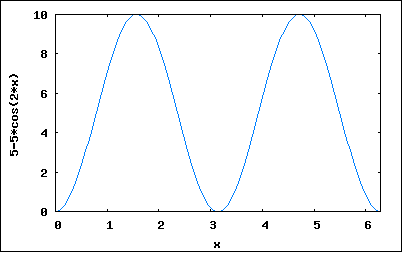 ちょうどEm^2/(2*RL)だけ正弦波を正側にシフトしたような波形になることが直感的にわかる。 それと意外なのが電力の波形は電源の周波数の倍の周波数で変化するという点である。これは正弦波同士を掛け算すると互いの周波数を加えたものと引いたものの2つの周波数の成分が生じるということを意味する。これは高周波でよく使われる周波数変換の原理でもある。 sin(x)*sin(2*x)と基本周波数とその2倍の周波数の正弦波を掛けた場合、 (%i15) sin(x)*sin(2*x); (%o15) sin(x)*sin(2*x) 合成波形をグラフにプロットすると (%i16) wxplot2d([sin(x)*sin(2*x)], [x,0,2*%pi])$ 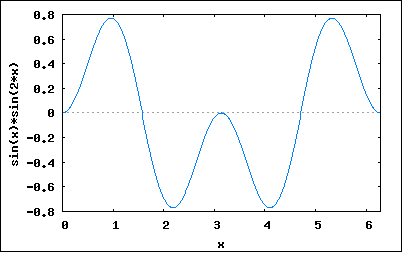 妙な波形になるがMaximaで式を整理すると (%i24) trigreduce(%); (%o24) cos(x)/2-cos(3*x)/2 掛け合わせた周波数の差と和の2つの周波数成分から成っていることがわかる。 |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| » |
webadm | 2007-11-14 5:51 |
| 投稿するにはまず登録を | |

