| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2012-4-15 0:24 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3107 |
LC並列回路 今度はLC並列回路に関する問題。
スイッチをt=0で閉じたとき電流が振動的となるための抵抗Rの範囲およびそのときの固有周波数を求めよ。 というもの。 LC並列回路と直列に抵抗Rが接続された回路にステップ入力が加わると考えることができる。 2つの閉回路に関してキルヒホッフの電圧則により以下の関係式が成り立つ これをHeaviside演算子とベクトルで書き直すと これを演算子法で解くと ということになる。 新たに以下の演算子変換対を用いた 上記の解でべき根が実数である限りは振動的ではない。従って電流が振動的になるのはべき根が虚数となるケース ということになる。 ちなみにそのケースの解は ということになる。 従って固有周波数は ということになる。 R=C=L=E=1でプロットしてみると 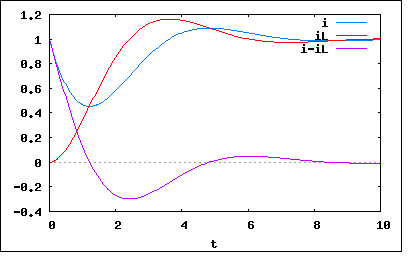 ということになる。 手元の回路シミュレータで同じ回路をシミュレートしてみると 厳密解とよく一致している。 P.S 解の検算にはMaximaを使用した。Maximaで以下の連立微分方程式を初期値問題として解くことができる。 desolve([R*diff(i(t),t,1)+(i(t)-i[L](t))/C=0,(i(t)-i[L](t))/C-L*diff(i[L](t),t,2)=0],[i(t),i[L](t)]); を実行すると Is L*(4*C*R^2-L) positive, negative, or zero? と尋ねられるので、nと答えると過減衰のケースの解が得られる。 表示された一般解の式に初期条件を代入するため subst(0, i[L](0), %); subst(E/R, i(0), %); subst(0, at('diff(i[L](t),t,1),t=0), %); expand(%); を実行すると演算子法で得たのと等価な式が得られる。 同様にpと答えて初期条件を代入すれば、振動的なケースの解が得られる 便利である。 |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| |
webadm | 2011-11-1 17:19 |
| |
webadm | 2011-11-1 17:32 |
| |
webadm | 2011-11-3 5:24 |
| |
webadm | 2011-11-3 6:23 |
| |
webadm | 2011-11-3 8:44 |
| |
webadm | 2011-11-3 15:53 |
| |
webadm | 2011-11-3 16:32 |
| |
webadm | 2011-11-4 1:09 |
| |
webadm | 2011-11-4 2:29 |
| |
webadm | 2011-11-4 7:48 |
| |
webadm | 2011-11-5 10:47 |
| |
webadm | 2011-11-5 20:42 |
| |
webadm | 2011-11-6 1:32 |
| |
webadm | 2011-11-6 2:44 |
| |
webadm | 2011-11-6 6:17 |
| |
webadm | 2011-11-8 5:08 |
| |
webadm | 2011-11-8 7:42 |
| |
webadm | 2011-11-10 7:26 |
| |
webadm | 2011-12-29 5:39 |
| |
webadm | 2012-1-11 8:53 |
| |
webadm | 2012-1-11 10:52 |
| |
webadm | 2012-1-14 21:44 |
| |
webadm | 2012-1-22 3:04 |
| |
webadm | 2012-1-22 23:50 |
| |
webadm | 2012-1-23 1:37 |
| |
webadm | 2012-1-23 4:15 |
| |
webadm | 2012-1-24 9:31 |
| |
webadm | 2012-1-27 7:27 |
| |
webadm | 2012-1-29 0:18 |
| |
webadm | 2012-1-29 0:45 |
| |
webadm | 2012-2-4 9:41 |
| |
webadm | 2012-2-7 6:22 |
| |
webadm | 2012-2-10 9:18 |
| |
webadm | 2012-2-12 20:06 |
| |
webadm | 2012-2-12 23:06 |
| |
webadm | 2012-2-14 7:38 |
| |
webadm | 2012-2-14 8:48 |
| |
webadm | 2012-4-5 10:59 |
| |
webadm | 2012-4-10 8:07 |
| |
webadm | 2012-4-11 15:26 |
| |
webadm | 2012-4-14 6:36 |
| |
webadm | 2012-4-14 17:43 |
| » |
webadm | 2012-4-15 0:24 |
| |
webadm | 2012-4-16 3:54 |
| |
webadm | 2012-4-17 9:05 |
| |
webadm | 2012-5-5 18:09 |
| |
webadm | 2012-5-5 23:12 |
| |
webadm | 2012-5-6 19:26 |
| |
webadm | 2012-5-6 19:53 |
| |
webadm | 2012-5-6 21:41 |
| |
webadm | 2012-5-7 2:09 |
| |
webadm | 2012-5-8 8:31 |
| |
webadm | 2012-5-12 18:14 |
| |
webadm | 2012-5-13 1:37 |
| |
webadm | 2012-5-13 22:24 |
| |
webadm | 2012-5-13 23:03 |
| |
webadm | 2012-5-14 8:11 |
| |
webadm | 2012-5-19 19:10 |
| |
webadm | 2012-5-23 4:47 |
| |
webadm | 2012-5-28 23:28 |
| |
webadm | 2012-8-3 7:14 |
| |
webadm | 2012-8-4 23:52 |
| |
webadm | 2012-8-5 2:55 |
| |
webadm | 2012-8-6 21:08 |
| |
webadm | 2012-8-8 7:41 |
| |
webadm | 2012-8-8 9:30 |
| |
webadm | 2012-8-11 20:51 |
| |
webadm | 2012-8-11 22:35 |
| |
webadm | 2012-8-11 23:00 |
| |
webadm | 2012-8-12 3:28 |
| 投稿するにはまず登録を | |

