| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2012-5-14 8:11 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
RC直列回路(交流入力) 今度はRC直列回路の交流入力に関する問題
図のようなRC直列回路にt=0から正弦波電圧e=Em sin(ωt+θ)を加えるとき、抵抗RおよびキャパシタンスCの端子電圧はどうなるか。また過渡現象を生じないための条件を示せ。ただし、この回路は静止状態であるとする。 というもの。 以前のRL直列回路と異なるのは問われているのが電流ではなくRとCの端子電圧である点。それと静止状態とは、Cの初期電荷が0ということだと解釈しよう。 抵抗Rの端子電圧VrとキャパシタンスCの端子電圧に関して以下の関係が成り立つ ということになる。 これをHeaviside演算子とベクトルで書き直すと これを演算子法で解くと ということになる。 ω=C=R=Em=1としてプロットしてみると 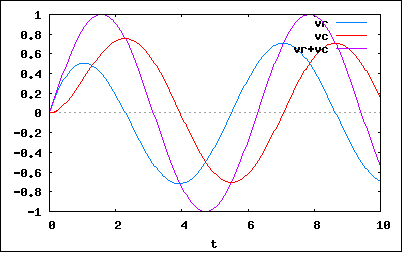 ということになる。過渡現象が現れているのが見てとれる。 回路シミュレーターの結果も厳密解と一致している。 従って過渡現象を生じない条件は、上記の解の過渡項が消滅すればよいので ということになる。 ω=C=R=Em=1のケースではatan(1/ωCR)=φ=π/4であるので、上記の条件を満たすθはπ/4と5π/4ということになる。 θ=π/4としてプロットしてみると 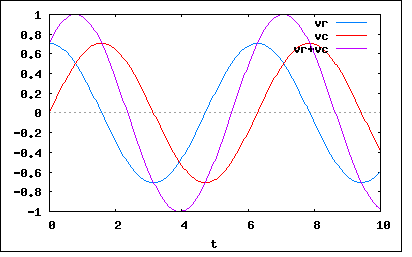 綺麗に過渡現象が消滅し定常状態と変わらないのが見てとれる。 回路シミュレーターの結果も厳密解と一致している 著者は何を勘違いしたか、題意で求められている電圧ではなく電流の解を求めてしまっている。過渡現象が起こらない条件はあっているが、これだと点数は半分しかもらえない。 P.S 部分積分を計算した後、分母の(ωCR)^2+1を開平して係数として残るようにしないと振幅がωや素子定数に依存しないという誤った解が導き出されてしまう。このあたりが演算子の非可換性と併せて演算子法の落とし穴でもある。解法としてはストレートで線型代数による連立方程式の解法とシームレスにつながるのだが注意を怠り安易な道を選択すると落とし穴に墜ちる。この辺りは後にLaplace変換を学ぶ際にでも整理することにしよう。 この種の問題の解を実際の回路と測定器だけを使って試行錯誤的に見いだすのは困難である。例えある素子定数での条件が見いだされたとしても、それと異なる素子定数での解はその結果から直接導くことはできない。解析的な手法が依然として不可欠なのはこの理由による。 |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| |
webadm | 2011-11-1 17:19 |
| |
webadm | 2011-11-1 17:32 |
| |
webadm | 2011-11-3 5:24 |
| |
webadm | 2011-11-3 6:23 |
| |
webadm | 2011-11-3 8:44 |
| |
webadm | 2011-11-3 15:53 |
| |
webadm | 2011-11-3 16:32 |
| |
webadm | 2011-11-4 1:09 |
| |
webadm | 2011-11-4 2:29 |
| |
webadm | 2011-11-4 7:48 |
| |
webadm | 2011-11-5 10:47 |
| |
webadm | 2011-11-5 20:42 |
| |
webadm | 2011-11-6 1:32 |
| |
webadm | 2011-11-6 2:44 |
| |
webadm | 2011-11-6 6:17 |
| |
webadm | 2011-11-8 5:08 |
| |
webadm | 2011-11-8 7:42 |
| |
webadm | 2011-11-10 7:26 |
| |
webadm | 2011-12-29 5:39 |
| |
webadm | 2012-1-11 8:53 |
| |
webadm | 2012-1-11 10:52 |
| |
webadm | 2012-1-14 21:44 |
| |
webadm | 2012-1-22 3:04 |
| |
webadm | 2012-1-22 23:50 |
| |
webadm | 2012-1-23 1:37 |
| |
webadm | 2012-1-23 4:15 |
| |
webadm | 2012-1-24 9:31 |
| |
webadm | 2012-1-27 7:27 |
| |
webadm | 2012-1-29 0:18 |
| |
webadm | 2012-1-29 0:45 |
| |
webadm | 2012-2-4 9:41 |
| |
webadm | 2012-2-7 6:22 |
| |
webadm | 2012-2-10 9:18 |
| |
webadm | 2012-2-12 20:06 |
| |
webadm | 2012-2-12 23:06 |
| |
webadm | 2012-2-14 7:38 |
| |
webadm | 2012-2-14 8:48 |
| |
webadm | 2012-4-5 10:59 |
| |
webadm | 2012-4-10 8:07 |
| |
webadm | 2012-4-11 15:26 |
| |
webadm | 2012-4-14 6:36 |
| |
webadm | 2012-4-14 17:43 |
| |
webadm | 2012-4-15 0:24 |
| |
webadm | 2012-4-16 3:54 |
| |
webadm | 2012-4-17 9:05 |
| |
webadm | 2012-5-5 18:09 |
| |
webadm | 2012-5-5 23:12 |
| |
webadm | 2012-5-6 19:26 |
| |
webadm | 2012-5-6 19:53 |
| |
webadm | 2012-5-6 21:41 |
| |
webadm | 2012-5-7 2:09 |
| |
webadm | 2012-5-8 8:31 |
| |
webadm | 2012-5-12 18:14 |
| |
webadm | 2012-5-13 1:37 |
| |
webadm | 2012-5-13 22:24 |
| |
webadm | 2012-5-13 23:03 |
| » |
webadm | 2012-5-14 8:11 |
| |
webadm | 2012-5-19 19:10 |
| |
webadm | 2012-5-23 4:47 |
| |
webadm | 2012-5-28 23:28 |
| |
webadm | 2012-8-3 7:14 |
| |
webadm | 2012-8-4 23:52 |
| |
webadm | 2012-8-5 2:55 |
| |
webadm | 2012-8-6 21:08 |
| |
webadm | 2012-8-8 7:41 |
| |
webadm | 2012-8-8 9:30 |
| |
webadm | 2012-8-11 20:51 |
| |
webadm | 2012-8-11 22:35 |
| |
webadm | 2012-8-11 23:00 |
| |
webadm | 2012-8-12 3:28 |
| 投稿するにはまず登録を | |

