| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | 下へ |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2015-2-3 12:47 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3107 |
自分の数学を持つことの勧め 電磁気学とは直接関係ないタイトルだが(といって無関係なわけでもない)
常日頃、通勤電車や外食先のテーブルで数学書を読むわけだが、やはり人の数学というものはいくつかの理由ですんなり理解できるわけがない ・著者の持つ数学的な知見と比較し、読む側があまりにも知らないことが多すぎるための困難 ・近代の数学書では当たり前の、局所的な議論は最小限にとどめ大観的な議論が主体となるため、天下り的で退屈してくる これらの理由は大半の人が該当するだろう(その人が大数学者でない限り) ではどうしたら数学書がおもしろく読めるようになるかというと、上の最初の困難を緩和するしかない。 つまり自分でもある程度局所的な観点での知見を抱負に持ち、大観的な視点だけ欠如している状態でそれらの書物を読めばちょうど補完的な関係で、「ああ判った」ということにつながるはずである。 ではそういった知見はどうやって身につけるかというと、もはや人が書いたものを読むことでは得られない。 そこで自分の数学を持つということにつながる。 数学が苦手の人やどうもよく判らないという人は、自分の中に数学があるからだと考えたほうが納得がいく。つまり自分の数学の芽から見るとどうにも納得がいかない、ギャップが大きすぎるというわけである。 ギャップを縮めるには自分の数学を成長させるしかない。 ここでも再度、読んでいて退屈したり、自分で考えることを放棄させるようなテキストは絶対に読まないことを勧める。 具体的な例を挙げれば、教わってもそれを理解してもただそれだけに終わりなんら発展性のない公式がある。代表的なものには二次方程式の解の公式である。 確かに希ににこの公式を使って計算する機会が一生に一度ぐらいあるかもしれないが、ただそれっきりである。 昔一緒に仕事をした同僚と数学の話をする機会があって、最初に学んだもっともつまらない公式ということで意見が一致した、むしろそれを導出する際に使う「平方完成」もしくは「完全平方」というテクニックのほうが、その後も頻繁に使う機会があるという意見も一致した。 上の公式を見てもどうやって導出するのか思い出せない人も多いと思う。それが悲しい現実である。 平方完成とは、公式の元になった二次方程式をべき根を含む多項式の積に分解することである。 従って上の方程式が成り立つためには のいずれかが成立すればよいことになる。 上の条件式から解は ということになる。 この結果そのものが役立つ機会はほとんどないと思われるが、それを導出するのに使用した完全平方のテクニックは数式計算で度々お世話になることになる。 ただこれでも二次方程式を局所的に理解しただけで、他の数学とのつながりがまったく感じられず自己発展性も見いだせない。 しかしそうだろうか? 先の一般的な二次方程式を別の観点から見つめ直すと、教科書や学校では教えないおもしろい性質を再発見することができる。 二次方程式を以下の様に書き直してみると 上の関係が成り立つには が成り立てばよいことになる。 これは以下の様に書き直すと二次方程式の解の奇妙な性質があらわになる これはつまり、ある関数fにxを与えた場合、その結果がxのまま変化しないのが解であるということになる。 数学的には関数fは点xに作用して別の点へ移す写像と考えることが一般的である。つまりある写像に対して自分自身に移すような点xが二次方程式の解ということになる。 こうした点の集合が方程式の解ということになる。 このことは二次方程式にとどまらず、微分方程式にもあてはまる。 もちろん当てはまらないものも出てくるが、それを自分で調べるのは楽しい。そうやって局所的な議論を積み重ねると、もっと一般的な、大観的にシンプルにまとまらないかという思いが出てくる。つながるものはみんなつなげて一つになれば覚えやすいし扱いやすい。 そうやっていろいろ自分の数学を育てた後に、先人の書いたテキストを読むと目から鱗ということもあるし、つながりの無いばらんばらんな議論の寄せ集めでしかなかったと判明したりもする。 すくなくともこれは紙も鉛筆もなくてもできることが多いし、目をつぶって半分眠りながらでもできる。おすすめである。 |
| webadm | 投稿日時: 2015-3-16 10:45 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3107 |
Re: 自分の数学を持つことの勧め 3月になると納品ラッシュが続いて、職場ではあちこちで火が噴いているのはいつものこと。
火消しに廻るので忙しくてこちらの投稿も開店休業状態で申し訳ない。 それでも通勤電車の中では解らないながらもいろいろへそ曲がりな視点で電磁気学を見直しているところ(といったら格好いいかも) 電磁気学の式では4πというのがよく登場する。というのも現代のcoulombの法則の式に出てくるわけだが、これは点電荷を中心とする半径rの球面の面積で中心電荷を割ったものが球面上の電位勾配(電界)に等しくなるように後に定められた定義だ。単位系の策定の歴史とも関係するので実は本質的ではない。 しかし半径rの球の表面積の式を導出せよと言われると実は困ったことになる。それ以前に半径rの円盤の面積(半径rの球を真っ二つに切った場合の断面の面積)の式を導出せよと問われても小学生の時に習った記憶しかない。実はそれ以降まともに導出したという記憶がないのだ。 これはさすがにまずいだろう。小学生の時の円の面積の導出方法は直感的だがよく考えられていて突っ込まれても大丈夫な方式だったはず。円盤を放射状にミカンの房のような部分に分割し、分割を無限に多くすればミカンの房のひとつひとつは半径rを二等辺とする無限小正三角形とみなすことができる。それをばらばらに分解して、平行四辺形状になるように向きを互い違いにして敷き詰めれば面積は底辺が円周の半分でπrで高さがrの平行四辺形(ほとんど長方形とみなしてもかまわない)になるので、面積は底辺×高さ=πr^2ということになる。 円の面積の厳密な証明というのは見たことがないが、ちゃんとやると小学生には理解不能なレベルだと思われるので、苦肉の策だと想像がつく。 ミカンの房がその中心角が無限小になれば、底辺が中心角×半径で2辺が半径の正三角形に近似できるというのはなんとなくわかる。これはr sinθをθを無限小dθに近づけた時にr dθに限りなく近づくというのは簡単に証明できるし、あちこちでよく見かける。 そうすると円の面積はこの微少の正三角形で円を埋め尽くしたと考えればよいので積分計算で求めることができる。 微少の正三角形の面積は底辺×高さ/2だから(1/2)r^2 dθ 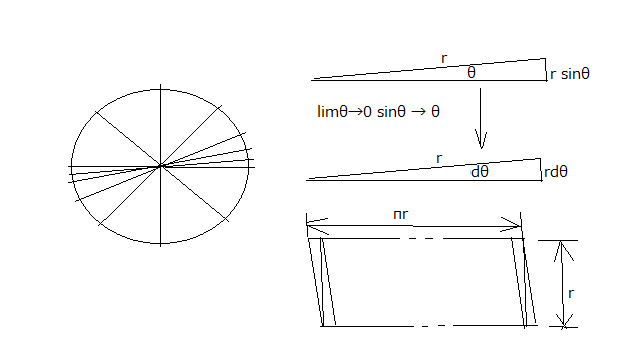 dθを0〜2πの範囲で積分すれば ということになる。 さて次は球の表面積だけど、小学生の時のように同様に今度は微少な正三角錐で球を敷き詰めたと考える方法を良く見かける。それは球の体積を求めるには都合が良いが、球の表面積を求めるのにはそこまでは必要ないかもしれない。 球の表面を微少な帯で敷き詰めればよいわけで、微少な帯の幅はrdθ、帯の長さは2π r sinθ dθとなる。従って微少な帯の面積は2π r^2 sinθ dθということになりθに関して0〜πまで積分すればよい。 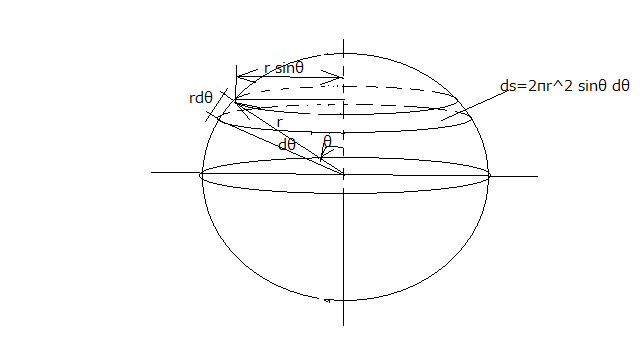 これはすぐに計算できて ということになる。 これでもぐりと言われないですむかもしれない。 同様に球の体積は上記の式をrに関して0〜rで積分すれば簡単に得られる。これはミカンの皮を球の中心からずっと敷き詰めて重ねていけば体積と等しくなると考えてよい。 ということになる。 なんだ簡単じゃないか(´∀` ) ただ自分数学ではおそらく微積分とか三角関数という概念を独自に再発見できるこは思えないので(再発見できたとしたら天才かも)ので、やはりちゃんとしたテキストを読んで一度は学ぶ必要がある。あのフィールズ賞数学者の小平邦彦ですら微積分の概念は学校で教わるまで知らなかったと言っているぐらいだし。 もっと数学的に遊ぶには、4次元の球の面積や体積とか求めてみるとおもしろい。それは読者の課題としよう。 P.S 実は球の面積が話題になったある半導体製造技術のニュースを話題にしたときに、現在の半導体がシリコン結晶の四角い板の上に回路を構成しているのを、球面状に構成すれば面積が増えてより多くの回路を集積できるという数値的な説明をするのに、球の面積の公式をとっさに書いたのだが、実はそれは間違っていて球の体積の公式だったということがすぐにばれて赤面した覚えがある。まあ内輪の議論だったのでそれで事なきをえたが、この時点で数学的な知識がだいぶ怪しいものだという印象を与えてしまったことは悔やまれる。まあお里が知れただけなんだけどね。 |
| webadm | 投稿日時: 2015-3-17 9:57 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3107 |
Re: 自分の数学を持つことの勧め 円の面積や球の表面積を考え出すと、幾何学的にいろいろな遊びをしてみる機会が得られる。
例えば、円の面積を考えた時に円盤を描いたが、以下のようにちょっとへそ曲がりな計算をすると、とんでもない発見をすることになる。 円周の任意の点の接線に垂直な長さ1の法線と同じ点から円の中心軸までの距離を辺とする平行四辺形の面積を考えるとそれはr sinθcosθということになる。θは中心軸と任意の点と円の中心を結ぶ半径のなす角である。 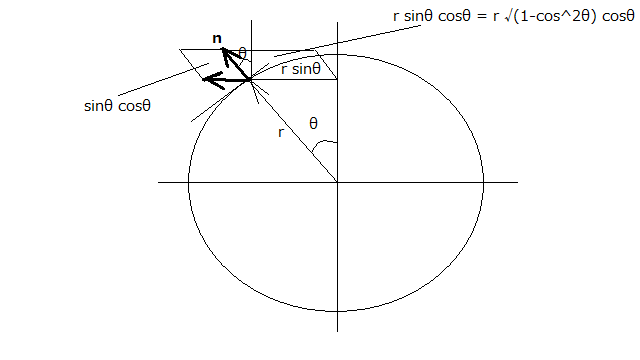 また任意の点から中心軸に垂直に結ぶ線と平行な長さ1の線分と先の法線とで構成される平行四辺形の面積はsinθcosθである。 実はこれ前に研究したLaplace方程式の解である球調和関数(球関数)のひとつである。球を考えなくても平行四辺形の面積を計算すると球調和関数が出てくるのは不思議である。この式はいったいどんな物理量を意味しているのだろうか。 少し見方を変えて、今度は回転軸と直交する線と任意の点と中心を結ぶ半径のなす角をΨとすると 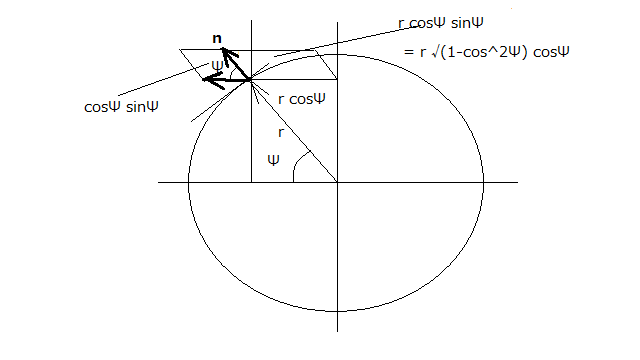 やはり球関数が出てくる。 球調和関数は定義域の両端で値0をとる(Legendre倍関数の性質による)のでMaximaを使用して極座標でプロットすると 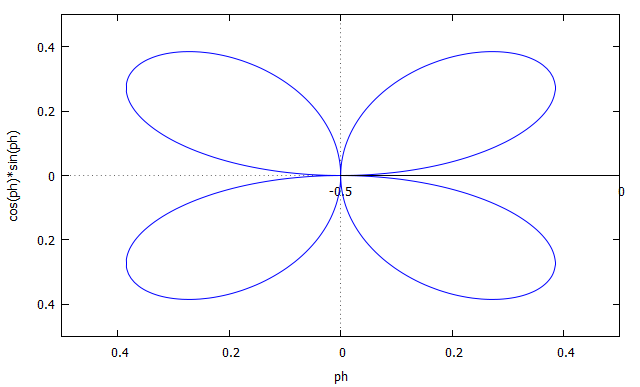 という4つ葉のクローバーのような文様が現れる。 これを軸対称な球座標でプロットすると 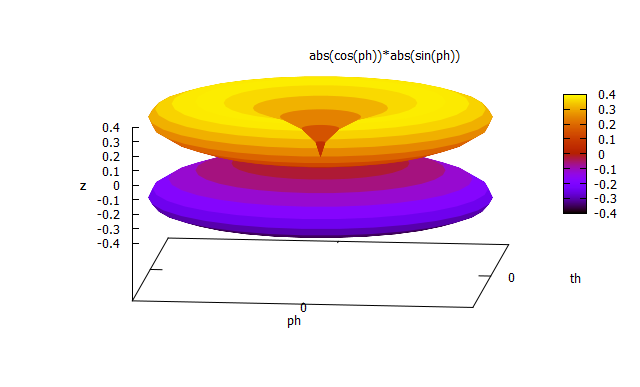 4つ葉のクローバーを中心軸を軸に回転させたような形になる。小学生の時に国語の教科書に載っていた、ちびくろサンボの物語に虎が木の周りをぐるぐる駆け回っていると最後には黄色いバターだかなんかになったという下りを今も思い出す。その後差別用語を使っているということで発禁になり教科書から削除されたらしい。 これもLaplace方程式の解のひとつであり、静電ポテンシャルの一例である。 これが何を意味するか突き止めるのは読者の課題としよう(´∀` ) |
| webadm | 投稿日時: 2015-4-15 21:41 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3107 |
Re: 自分の数学を持つことの勧め ふう、先々週の金土日と朝から終電まで合同デバッグと称する作業を強いられて集中力を使い果たして、今ごろその後遺症に悩まされ中(;´Д`)
ある種PSDTなのかも。緊張を解きほぐせるのは昼食時だけで、それ以降は夕食も抜きで緊張を強いられるというストレスを解放するタイミングがなかったのが痛い。みんな真面目な人ばかりだとそういうことになりかねない。 さて、だいぶ間が開いてしまったが、通勤途中とかではもっぱら自分数学の探究を続けている。 自分数学の何が楽しいかは、前回を例にすると、今も目の前に生きている数学的対象を観察してその正体を探求することにつきる。 数学書とかで扱われている数学的対象は、研究し尽くされた動物の剥製標本を眺めている感じがして興味が失われる。それが数学嫌いを生む原因ではないかと思う。 ちょうど子供に寿司屋でマグロのにぎりを前にして「お嬢ちゃんこれがマグロというものだよ」と説明するようなもので、確かにマグロの都合の良い性質だけとらえているけれども、その外観から本当のマグロが大海で泳ぎ回っている姿を想像することは困難だろう。 それと同様に数学書で扱われている数学的対象も、都合の悪い部分はそぎ落とされていることが多いし、それが現実に存在するのかどうかも怪しい。 以前に球座標系のLaplace方程式の解として現れるLegendre倍関数を学んだが、確かにそれは自然に出てくるのだが、現実世界でそれが存在している姿を想像するのは難しい。電磁気学では誘電体中の電界を考える時に微少な電気双極子がびっしり並んだ状態を想像すればなんとか存在する気もするけど、それは想像にすぎない。 前回の記事で単純な円周上の任意の点の法線ベクトルと中心軸からの距離ベクトルがなす平行四辺形の面積がまさにLegendre倍関数であることを再発見した。これは現実に目の前に存在して今も生きているのは明らかである。何故こんなところにLegendre倍関数が生きているのかは読者の課題とした。 生きた数学的対象を見ると、子供が動物園につれていかれて生きた動物の姿を初めてみた時と同じ衝撃がある。生きていない剥製標本の動物をみるのとは大違いである。 さて、他にも生きた数学的対象を見いだすことはできないだろうか? テキストとかでは、ちらっとわかりやすい例としてそうした生きた数学的対象を持ち出す著者も居る。しかしそれは読者の興味を誘う手段であって、それを研究することが目的ではなく、次は研究しつくされた数学的対象の剥製標本について説明するだけである。 小学校の授業で今も記憶に残るのは、国語のテストで引用されている既存の小説の一節を読んで、設問に答えなさいという典型的な問題である。小説の一節があまりにおもしろいので(生き生きとした表現なので)その世界にすっかり引き込まれてしまい、あれこれ想像を巡らしてテスト用紙では割愛されている続きのシーンを思い描いたりしていて、結局問題には答えずにいつも0点を頂戴していた思い出である。 学習指導要領的には文章を読んでその内容を正確に理解するという能力を確かめるテストなんだろうけど、読む手には文章をいかようにでも解釈してよいという自由が与えられているはずだが、テストではその自由は奪われていて、出題者と同じまったく同じ解釈をしなければ0点ということになる。このことを子供ながら瞬時に察して、以降は国語のテストでは小説の一節を存分に味わって問題には答えないという姿勢を貫いた覚えがある。 自分数学も同様で、テキストに書いてあるのはその著者の自分数学であって、私の自分数学とは違う。他人の自分数学を理解するのは苦痛だが、自分の数学を探究するのは楽しい。 さて、自分数学の次なるネタを探そう。 複素解析を学んだ際に、最初に躓くのが虚数単位iである。 歴史的には√-1という形で二乗すると-1になる数という形で登場したが、長らくその数学界での定位置が与えられていなかった。 線形代数の行列表現を使用すると、虚数単位も行列の中の一つとしてとらえることができる。そうした比喩は理解を助けるためにテキストでも用いる著者は多い。しかし、更に深追いすることはなくて、読者の気をひきつけるためだけである。 例えば、実数値は以下の様に行列で表現できる ここでrは任意の実数値である。 虚数単位iは二乗すると-1になり、三乗すると-iになり、四乗すると1になり五乗するとiに戻る。 これはちょうどベクトルを原点を中心に90度づつ回転させたような位置関係になることから、虚数単位iが位置する座標は実数軸と直交した座標軸上にあると考えることができる。 行列ではちょうど座標軸の回転させる変換行列がそれに相当する。 試しに二乗してみると 確かに実数の-1になる。 従ってテキストでは複素数は実数と虚数の任意の線形結合で表されることになると締めくくるのが普通である。 教科書ではそこまでしか書いてないが、ここに想像から生まれたのではあるが、生きて目の前に居る獲物を見てそのまま立ち去るというのは忍びない。 自分数学的には、虚数単位iのように回転作用のある数は他にはないのだろうかという疑問が沸く。 それはある程度Hamiltonの四元数が頭にあってのことだが、Hamiltonの四元数発見までの長い労苦を追体験したいというわけではなく、目の前の獲物をいろいろな観点から観察したいという自然の欲求である。 例えば、教科書では説明されない、以下の行列の表現は一体何を意味するのだろうか、もしくは何も意味しないのだろうか? これは二乗すると 三乗すると また元に戻るという変な性質を持つことがわかる。 どうも成分が4つの二次元行列では別の虚数単位に相当する数は出てきそうも無い気がする。 3次元行列にするか、立体行列に拡張しないとだめくさい。 3次元行列は当たり前過ぎなので、テキストには出てこない立体行列というものを想像してみよう。 ちょうど立方対の頂点にそれぞれ成分が位置するとして、6つの二次元行列で囲まれている感じ。成分は8つあるので、その中から4つの成分の組み合わせで二次元行列がいくつできるか考えてみると卒倒する。 さてその中には同じ成分の組み合わせだが二次元行列を回転したり、転置したようなものも含まれるわけで、それらが同じ行列と見なすべきかどうか悩ましい。 それらの中に果たして虚数単位のようなものは存在するのだろうか?はたまたHamiltonの四元数は構成できるだろうか? それを調べるのは読者の課題としよう(´∀` ) P.S 4つの成分の二次元配列でも、成分を実数ではなく複素数からとれば四元数の基底に対応する結果が得られる。 先の二乗すると単位行列になる変な行列は要素が実数だったが、虚数単位√-1を乗じれば、二乗すると-1に対応する行列になる ここで2つの二乗すると-1に対応する行列になるものが見つかったので、その二つを掛けるとまた別の線形独立な基底行列が現れる これもまた二乗すると-1に対応する行列になる 掛ける順序を逆にすると結果の符号が変わる i,j,kはそれぞれ線形独立であることは容易に確かめることができる。従って四元数はスカラー項に相当する単位行列と、i,j,kの三つの基底行列の任意の線形結合に対応する(複素数を元とする二次元行列)。 Hamiltonはこの四元数を発見するのに長い間かかってある日、橋の上で遂に発見に至ったという話は有名である。 上記の結果はWikipediaになにげなく書かれていたのを昨日見つけた。いいところまで辿りついていたのに、自分で発見できなかったのは残念だが、すぐ近くまでさまよっていたのでよしとしよう(´∀` ) このHamiltonの四元数は、後にベクトル解析や電磁気学に多大な進展を与えることになる。 |
| webadm | 投稿日時: 2015-4-21 10:25 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3107 |
Re: 自分の数学を持つことの勧め 電磁気学のテキストではベクトル解析の数学的な知識があることが前提としているものがほとんどだ(19世紀末とかまだベクトル解析が一般的ではなかった時代に出版されたものを除く)。
ベクトル解析の上に構築されているかのように見えて、電磁気学を学んでいるのかベクトル解析を学んでいるのか分からなくなってくる。 いつも躓くのはベクトル解析の常識が登場して、それに基づいて電磁気学の理論が解説される時だ。 このため最初の章で躓いて次ぎの章までたどり着けない。これは私だけではないだろう。 さて今日躓いたのは、たぶん常識的なことなんだろうけど、以前にも書いた並行四辺形の面積に絡んだ記述。 斜交する2つのベクトルa,bが作る並行四辺形の面積は となることだ。 こんなことがすぐに解るやつは頭おかしい、と考えるのはそんなこともすぐに解らないやつは頭悪いと言われる種族であることは確かである。さて貴方はどっちだろう。 電磁気学だけではないが、数学というのはシームレスにつながってはいない。突然まったくかけ離れたところに話が飛んでいってしまってついていけない人は落伍者となる。 普通に並行四辺形の面積というと、底辺x高さというのが小学校で習った知識である。 底辺を水平に平行に置いて、それに隣り合う辺が傾いている図を想像すると、傾きの角度がθであれば、2つの異なる辺a,bの長さを|a|,|b|とすれば、平行四辺形の面積は となるのは以前にも書いた。 幾何学的に表すと。 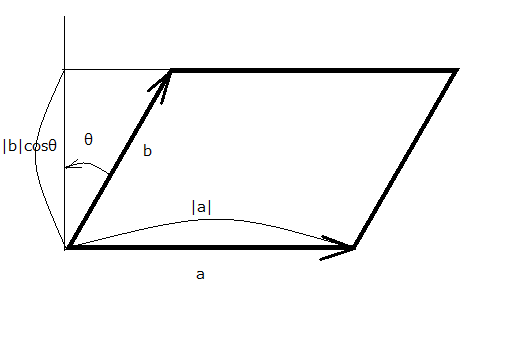 これと先の行列式で表された面積が等しいだなんてすぐには思いつかないし。 もちろん上の図で、ax=|a|, ay=0, bx=|b|sinθ, by=|b|cosθであるからして、行列式での面積の式と同値であることは確かである。 一般的な以下の並行四辺形ではどうだろうか? 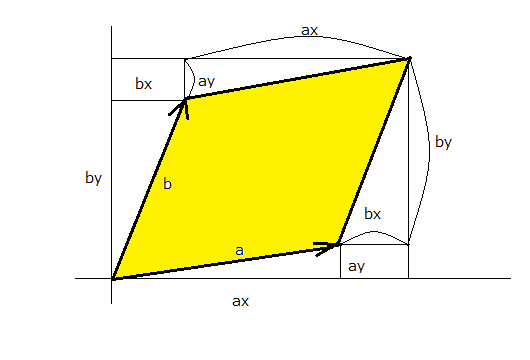 補助線をいくつも引いた結果から、黄色の平行四辺形の面積と対角的に接する一番大きな4角形の面積は 大きな四角形から問題の平行四辺形に含まれない余分な部分の面積は 従って黄色い並行四辺形の面積は、ベクトルa,bの成分で表すと ということでようやく理解できたことになる。 こんなの一瞬で解るほうが頭おかしい。 これ以外にも同じ結果の導出方法は沢山あると思われるが、それを確かめるのは読者の課題としよう(´∀` ) 実のところここはベクトル解析で基本中の基本の勘所な気がする。 P.S あとになって気付いたのは、積分の概念を知っていれば、もうひとつの見方で並行四辺形の面積が計算できるということ。 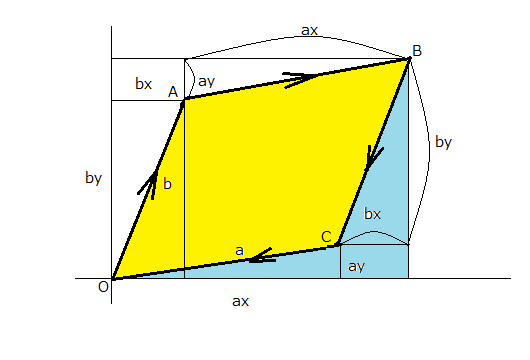 並行四辺形の外周の高さを並行四辺形の外周である閉路OABCOに沿って積分したものが平行四辺形の面積だと言える。 OABまではx座標が増加する方向にあるが、BCOは逆向きになるため積分結果の符号が変わる。 すなわちOABに渡って積分した値から、OCBに渡って積分した値を差し引けば並行四辺形の面積が得られるというわけである。 ということになる。 計算は面倒だが概念的にはこっちの方がすっきりする。 |
| webadm | 投稿日時: 2015-4-26 21:43 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3107 |
Re: 自分の数学を持つことの勧め ベクトル解析の入門書はいくつも購入して読んだものの、森さんの本を読んでも解ったようで実は良く解っていなかった。
やはり自分で考えるのが性に合っているかもしれない。 前回は斜交するベクトルが構成する並行四辺形の面積を考えたが、今度は同じ斜交するベクトルが構成するもうひとつの並行四辺形の面積を考えることにする。 え、斜交する2つのベクトルが構成する並行四辺形ってひとつだけじゃないのと考える方が多いがそれはもっともである。 今回はベクトルの内積について考えてみる。大抵の入門書では内積に関してページを割くのは1ページ以内で、外積についてはかなり慎重に説明しているのが普通である。なぜこうも扱いが違うのかというのを疑問に思っていたが、ベクトル解析の歴史を学ぶと理由がなんとなく分かってくる。 その前に、もうひとつの平行四辺形が存在する意味を明らかにしないといけない。 普通にベクトルの内積というと とか、 などと書かれる。 最初のは定義だと言われても、代数的に見通しが良いと言われても釈然としない。二番目は確かに並行四辺形の面積を表していることは解るがθの定義が曖昧だと前の記事で出した外積のときの並行四辺形の面積と区別がつかない。 最初の定義になんらかの幾何学的な意味があってよさそうだ。 実は前の記事で出した外積の場合の並行四辺形の面積の式と良く似ていることに気付く。 つまるところ上に示されるように成分としてb2,-b1を持つもうひとつのベクトルcと成す並行四辺形がすなわち内積だとも言える。 このもうひとつのベクトルcは実はベクトルbを90度回転したものであることは以下の関係から明らか。 これは前回Hamiltonの四元数を再発見した際に出てきた直交変換行列の片割れ(時計方向に大きさを変えずに90度回転)である。 幾何学的に見てみると 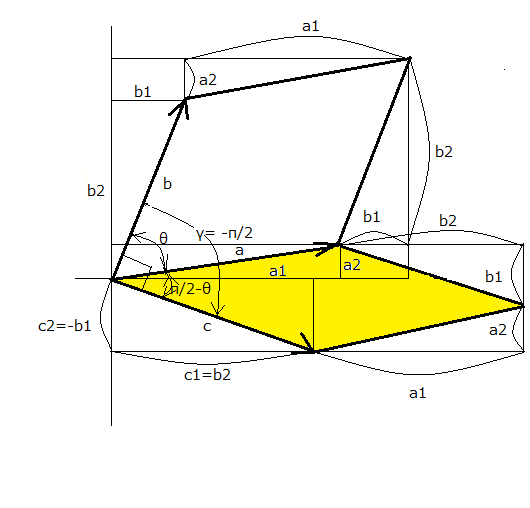 という具合にもう一つの並行四辺形が存在し、その面積が内積として定義できることがわかる。 こんなへそ曲がりな視点で書かれたテキストは世の中に存在するはずもない、自分数学の独断場である。 この関係から、ベクトルa,bが最初から直交して居るときには、もう一つの並行四辺形はぺしゃんこにつぶれてしまう(ベクトルa,cが線形独立でなくなる)ため内積は0ということがわかる。また逆も真なりで、ベクトルa,bが平行なら、その内積であるもうひとつの平行四辺形は直角形になり最大値を持つことになる。 これで内積とが外積が同時に理解できるじゃないか(´∀` ) 歴史的には19世紀のベクトル解析の暗黒時代にさかのぼる必要がある。 Hamiltonが四元数を見いだし、Maxwellが電磁気学の本を出版し、Heviesideがそれに魅了されて独学で研究を始めた時代である。 今日ベクトル解析で使われるスカラーやベクトルという用語は実はHamiltonが四元数を表した時に用いたのが最初である。後にベクトル解析学者はHamiltonの四元数を研究し、そして都合の悪い部分は捨てて都合の良い部分を採用したというまさにbootlegに限りなく近いことが行われた黒歴史がある。 ではHamiltonの四元数の何が都合が悪く、何が都合が良かったのだろうか? Maxwellも初版では四元数を用いようとしたために、結局のところ関係式をベクトル成分毎に記述するしかなかったが、没後の第二版ではそこは改められてベクトル解析よりの記述になっている。我々が今日目にすることができるのは後者の方で、Heavisideなどの同時代人が読んだのは初版本である。 Hamiltonの四元数は実数項から成るスカラー項と、それと互いに直交する3つの直交基底からなるベクトル項で構成される。 まずはスカラー項は0としてベクトル項だけでベクトルa,bを四元数で表すとして、その積を計算してみることにしよう。 ということになり、ベクトル項だけの四元数を乗じるとベクトル項以外にスカラー項が出てきてしまう。スカラー項はベクトルの内積の形をしている、ベクトル項は外積の形をしていることがわかる。 ベクトル項のかけ算からスカラー項が出てくるのは、Hamiltonが見いだしたベクトル項の基底の乗法則から当然の結果である。 19世紀のベクトル解析学者は、ベクトル項だけで事は済むはずだと考えて、Hamiltonの乗法則を以下の用に変更し、それをベクトルの外積の定義とした。 つまり並行な(線形従属な)ベクトルの間の外積は0とすることによって、ベクトル項の積からスカラー項を抹消することにしたのである。 従ってベクトル解析では というのが今日の定番となったわけである。 20世紀の後半になってようやくスカラー項が意味のある物理量を表すことが再発見されることになる。 |
| webadm | 投稿日時: 2015-4-29 20:10 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3107 |
Re: 自分の数学を持つことの勧め さて内積と外積とか実は光と影みたいな関係であることが判明したところで次なる謎が待ち構えている。
それは有向面積とか面積ベクトルとか、符号付き面積と呼ばれる概念であるが、そもそも面積に正と負の値があると言われた時点で混乱する。 小学生の時にそんなことは教わらなかったよね。 現実社会では面積というのは正の値しかないし。もし負の面積とやらがあったら、所有する土地の面積を合算で減らすことができて、固定資産税をチャラにできることになる。しかしそんなことは誰もできない。 これもどうやらHamiltonの四元数で考えた方がよくね? 例によってスカラー項は0で同一平面上にあるベクトル項だけの2つの異なる四元数Qa,Qbの積を考える。 ということになる。 すなわち同一平面上にある二つの四元数(もしくは同一平面に平行な二つのベクトル)の積はその平面と垂直な法線上にある四元数(もしくは法線と平行なベクトル)を生み出すことになる。 もちろん二次元ベクトルが存在する平面空間には平面以外の次元は存在しないので、平面に垂直なベクトルというのは定義できない。 そこでベクトル項の係数だけ着眼して、元の平面上の2つのベクトルから構成される平行四辺形の面積は2つのベクトルの成分値によっては正負どちらの値も取り得るので符号付き面積とか、有向面積という名前で呼ぶしかないわけである。 先の同一平面上の四元数のかけ算の順序を逆にすると ベクトル項の符号が反転する。つまり複素数で言う共役複素数のような共役四元数というようなものが出てくる。スカラー項の値は複素数の共役複素数の実数部と同様に同じで共役複素数間では変わらない。 今日のベクトル解析では以下の様に同一平面上にある2つのベクトルa,bの積の順序を変えるとベクトル項の符号が変わるから、並行四辺形の面積の符号が変わることを意味する。 これは普通のベクトル積の定義そのものであるが、これから以下の結論が得られる つまり面積に相当するベクトル項の係数に正負があるということになる。 大抵のベクトル解析の入門書では有向面積とかに関しての議論で、およそ数学的とは思えない幾何学的な説明の仕方で逃げているものがほとんどである。 例えば片方のベクトルを時計方向か版時計方向かどちらか少ない回転角度で回転して重なった時に時計方向だったら負で反時計方向だったら正とするとか。 もっともらしいのが、Flemingの右手の法則に習って右手系を正として左手系を負とするとか。 幾何学的には確かに図形の裏と表があるように、並行四辺形の場合も裏から見た並行四辺形と表から見た並行四辺形は、二辺の長さが違う場合には、同一平面上ではぴったりとは重ならない。重なるのはどちらか片方を裏返す必要があることから、面積に正負(裏表)が存在するというのは直感的には理解できる。 どうしてもベクトル解析の初歩を学ぶのは歴史的にも数学系ではなく物理系や工学系であるから代数には不慣れで、代数的に理解するということは期待できないのでそういう説明が伝統的になったのかもしれない。今日では線形代数をベクトル解析に先だって学ぶのが普通だから代数的な説明があってしかるべきだと思われる。こうしたところにも伝統の頸城から逃れ出ていない教育の一面がある。 代数的に考えた場合にはどちらを正にしても結果としては変わらないというのがわかる。それだと二通りの流儀ができて困るから統一的にどちらかを採択する必要がある。 どうすんだそれ(;´Д`) 考えてみるとベクトルを定義する空間そのものが有向でないと話が成り立たないことに気付いたりする。 二次元ベクトル空間では、二種類の向きの異なる空間が存在する。 幾何学的にはちょうど紙の裏と表みたいなもの。 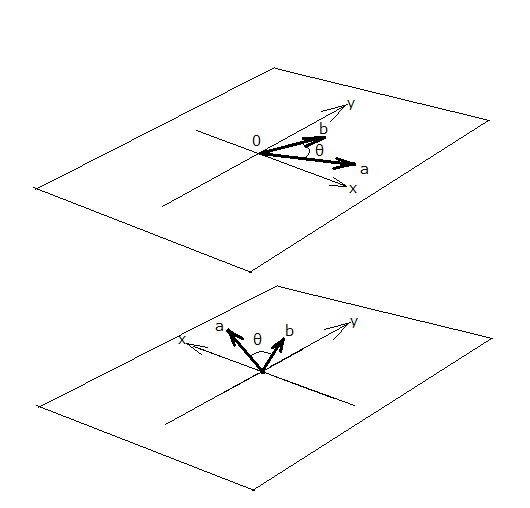 どちらか片方の平面を裏返して重ねると一致するというもの。 ただしどちらの平面上でも先のベクトル積の定義は成り立つ。 裏と表の違いはひとつの座標軸の奥行きがちょうど鏡に映したように逆向きになる点である。 つまり上の平面の左側にY軸と平行になるように垂直に鏡を置くと鏡の中に写って見えるのがちょうど下の平面になる。その逆もまた真なり。 このどちらかを正の向きを持つ平面とし、もう一つを負の向きを持つ平面としなければならないことになる。 実のところ二次平面上でこの種の議論をしても徒労に終わる。 上の2つの平面空間ではベクトルa,bが張る平行四辺形(もしくは三角形でもよい)の面積は同値であるからである。 同じ面積を持つのに唯一違うのは、上の平面では原点に立ってベクトルaの指す方向に向いた場合、ベクトルbは左手に見えるが、下の平面ではちょうどその逆で、ベクトルbは右手に見える。 なので二次元平面でa×bの有向面積の符号を定める時の規則として、aの方向に沿って進む時にbが左手に見える場合を正とすると定めているわけである。そしてその規則が成り立つ平面を右手系と呼び、他方を左手系と呼ぶことになっている。左手系では右手系と逆にbが右手に見える場合が正になる。 何度も言うように代数的にはどちらを正にして構わないのだが、両方の座標系が入れ替わり立ち替わり現れると混乱するのでどちらか一方だけを登場させるように決める必要があったわけである。 これも実は二次元空間では説明が苦しくて、三次元空間で議論しないと混乱する。何故なら先の説明でaに沿って進んだ時にbが左手に見えるのに何故右手系とするのかという素朴な疑問が生じるからである。 今度は三次元空間で同じ議論をしなければならないが、知恵熱が出てきたのでまた次の機会にしよう(;´Д`) P.S 互いに鏡に映したような持つ同じ組成で2つの異なる分子構造が実験室や自然界に存在する話は前にもしたよね。鏡像異性体というやつ。 これも前に書いたけど、学生の頃に化学の実験で解熱剤として知られるアスピリンを合成した際に、教授が「飲んだりしないように不純物が含まれているから」というように警告していたのが記憶に残っている。 何も工夫もせずに化学合成を行うと、同じ組成だが鏡像異方性によって異なる生理活性を持つ二種類の分子が均等の確率で生成される。片方は意図した通りの効能があるが、鏡に映したような構造のもう他方は意図した効能が無かったり害毒だったりする。 日本でも昔大変な被害をもたらしたサリドマイド事件も、原因はサリドマイドの合成時に効能がある方とは別の鏡像異性体が高い催奇性を持つことからサリドマイドを服用した妊婦から手足の指が未発達な奇形児が生まれるという被害が続出したことにより発覚した。 サリドマイドは良くも悪くも鏡像異性体に関して研究者は注意を払うようになったきっかけを生んでいる。それによって異なる二つの異性体の片方だけを選択的に合成する不斉合成技術の開発が急務となり、先日理研を止めた野衣さんはかつてその先駆的な研究でノーベル化学賞を受賞した人である。 |
| webadm | 投稿日時: 2015-5-5 5:33 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3107 |
Re: 自分の数学を持つことの勧め 二次元平面上で斜交するベクトルa,bの張る平行四辺形の有効面積に正と負がある議論の続きをしよう。
以前に平行四辺形の面積が積分で考えることができると書いたが、それを使うと二つの面積が定義できる。  これともう一つが 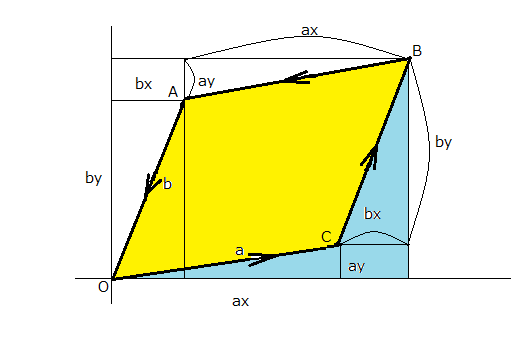 積分の方向を逆にしたので、互いに符号が異なるが絶対値は同じ平行四辺形の面積をとる。 これは当たり前の話である。 それではベクトルa,bを入れ替えた場合はどうなるだろう 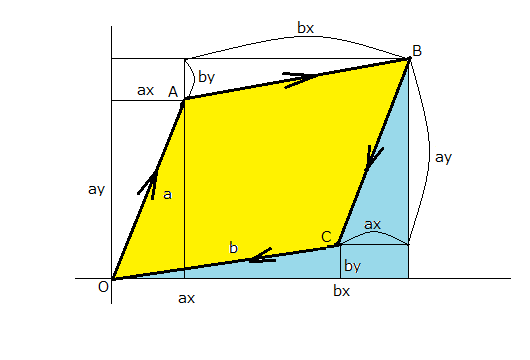 これは最初の面積のa,bを入れ替えたものだから面積は ということで絶対値は同じだがベクトルを入れ替える前と符号が異なる。 というわけで右回りと左周りの積分で符号が変わるのと、ベクトルを入れ替えると同じ方向の積分でも符号が変わるというのが確かめられる。 同じ原理を左手系に適用すると、話は逆になって右回りに積分すると負になり、左周りに積分しないと正の面積にならないことがわかる。 ところでこれはベクトルが張る象限の違いに影響するだろうかという疑問が沸いてくる。上の結果は第一象限については正しいが、他の象限や象限を跨いだ平行四辺形についても正しいのだろうか? それを確かめるにはベクトルを同じ角度だけ回転させても結果が変わらないかどうか確かめれば良い。 ベクトルをθだけ回転させる写像は以下の通りである これは以下の様に幾何学的に確かめることができる 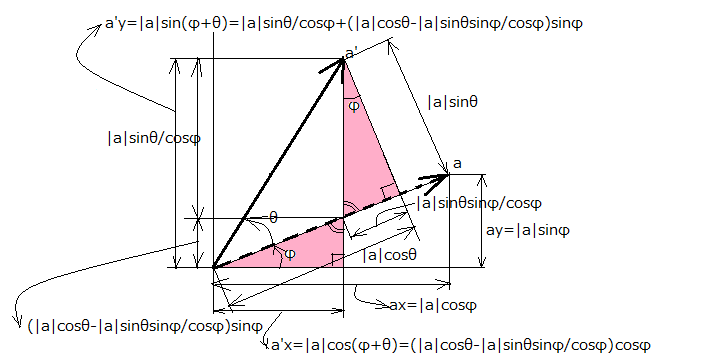 ということになる。 これは三角関数の加法定理そのものだけど、テキストで習う時にはそれは剥製で生きている対象ではないのですぐ忘れてしまいがちである。しかしベクトルの回転は生きた数学的な対象のまま目の前に存在するので、自分数学としては格好のターゲットである。 加法定理の公式を持ち出せば説明も要らないが、面白みもないし記憶にも残らなくなる。これならベクトルの回転と三角関数の加法定理がシームレスにつながっているので同時に理解できる。覚えやすいし、思い出し易い。というかこれ同じ事の言い換えじゃないのかという見方もできる。 さてこれで斜交する二つのベクトルa,bを任意の角度θだけ回転した場合に二つのベクトルが張る平行四辺形の面積がどうなるか計算してみればよい。 ということになる。 従って斜交する二つのベクトルが張る平行四辺形の有向面積は座標軸の回転に関して不変であることが確かめられた。 |
| webadm | 投稿日時: 2015-5-12 18:15 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3107 |
Re: 自分の数学を持つことの勧め さて二次元平面上の斜交するベクトルの積の結果は平べったい空間で正と負の向きを持つ有向面積というしっくり来ない結果をもたらすことは理解できたが、もうひとつ次元を増やした三次元空間上の任意の平面上の斜交する2つのベクトルの積を考えると、その真相がはっきりする。
簡単にするために三次元空間でx-y平面に平行で斜交する2つのベクトルの積を計算してみると 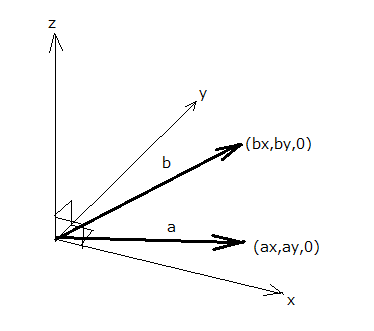 ということになる。 つまるところ三次元だと同一平面上の斜交するベクトルの積はベクトルが張る平行四辺形の有向面積の大きさを持つ平面に直交するもうひとつのベクトルを作り出すということになる。 二次元だと平べったい平面しか空間は存在しないので新たなベクトルを生成できないが、ベクトルの張る面積だけが定義できるという中途半端なことになる。 二次元と同様に上の関係式が成り立つもうひとつの三次元座標権が存在する。それは二次元の時と同様にちょうど鏡に映したような以下のような座標系である。 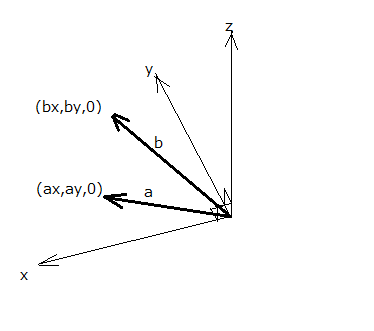 先の座標系は座標軸をどのように回転しても上の座標系とは一致しない。2つの座標軸は平行になっても、残りの座標軸の向きが反対になるのである。 しかし代数的には2つの座標系は同値であるから困ったことになる。 なので、前者をx軸を親指にy軸を人差し指として、中指をz軸に同じ向きになるようできるのは右手だけであるので右手系とし称して、逆に左手だけがそれが可能な後者の座標系は左手系と称する習わしになっている。 ベクトルの積がもうひとつのベクトルを生成する次元は限られていて、一次元と3次元と7次元だけであることが比較的簡単に証明できることが知られている。 ベクトルの積に関する局所的な議論はこのぐらいにしよう。 まだその先に躓きの石が待っている。 |
| webadm | 投稿日時: 2015-5-20 9:56 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3107 |
Re: 自分の数学を持つことの勧め ベクトル解析もしくは電磁気学を学ぶ上で初期の段階で遭遇するハザードは何かというと、それはベクトルからベクトル解析すなわちベクトル空間の微分積分にジャンプするところである。
歴史的な経緯から近代力学や流体力学では今やベクトルで速度や加速度、応力などをベクトルで表すのは当たり前になっているが、力学については19世紀になるまではベクトルという概念は存在しなかった。それらは19世紀以降に力学が再構成された際に書き換えられたものである。 Maxwell以前にも英国には静電気学の研究者が居てほとんど忘れられているか故人が発表せずにいたものがあり、それらは後生の人が偶然に発見して一般に知られることになる。 電磁気学の演習問題に以下の様な設問が無いのは何故だろう? 「電磁気学がそれ以前から知られている数学を用いて定式化をせずに、MaxwellはHamiltonの四元数を、HeviesideやHelzは独自のベクトル解析を編み出して定式化を行う必要があったのは何故か、簡単に説明しなさい」 これは何故ベクトル解析なのかという逆問題でもある。 前回まで議論してきた初等のベクトルに関する議論はおよそベクトル解析とはほど遠いものであるものの出発点としては妥当ものであることは確かだ。 しかしここまでの議論は位置ベクトルというか座標ベクトルの議論であって、それ自身はおよそ解析の対象ではない(微分積分ができない)。 解析というからには何らかの関数を成分としなければならないことになる。その関数が微分可能であれば解析が可能である。 微分積分なら力学の歴史上でとっくに登場しているので、それを何故Maxwellを始めそ後生のMaxwellian達が新たに定式化のために新たに数学を編み出さなければならなかったのはどんな理由があるのか。 それだけの道理がある理由があるはずである。 最初にはっきりするのは、Newtonの力学は質点の運動を数学的な対象として探求した結果と言える。空間には質点を除いては何も無いのと一緒で、単に質点の座標を与えるだけのものでしかなかった。すなわち絶対座標系というのが存在し、その原点は微動だ世界の中で動かないと考え、それとは別に慣性系という等速で移動する座標系を考える。やはりその座標系上には質点しか存在せず中間は何も存在しないし、質点には何らの作用もしないと考えられていた。 Newton力学では質点の座標は時間の関数として表され、時間と供に空間を移動する質点は速度を持つ、また速度も時間と供に変化すれば加速度を持つと考え、それらは共通して時間の関数である。空間は座標を与える尺度でしかない。 電磁気学はそれとは様相がまるで違っている。確かにcoulombはNewton力学の重力と同じ性質を静電気も持つと予想し、それを裏付ける実験を行った。今日の目で見れば、まともに予想を裏付けるデータが得られそうもない実験方法だったが、coulombは測定データを選別して、予想を裏付ける根拠に十分な結果を得た。今日的に見れば第三者による再現性がかなり低い論文だったと言えるが、結果的には間違っていなかったので今日もその名が刻まれている。 coulombが静電気がNewtonの発見した重力と似たようなものであると論文を書いたので、おおかたの研究者は、ああなんだ目新しいものは無いのか、じゃもう研究するのやめよう。と静電気の研究熱はそこで冷めてしまった。磁気に関する研究が欧州で活発になるのはその後の別の契機による。 Newton力学では質点間の互いの重力による作用のみを考えるだけで十分という暗黙の前提が存在する。しかし厳密には後にこれは修正されなければならないことになる。太陽とその周囲を回る衛星や彗星とかの運動を議論するにはそうした近似で十分説明できる時代の産物である。 その後天体運動の測定精度が高くなり、Newton力学では計算の誤差が説明できないぐらい顕著に表れるケースが出てきて何か理由があるとしか言えない時代がやってきた。 Einsteinの相対性理論がNewton力学の欠陥を埋めるものとして登場した。その際にMaxwellの電磁気学はそのまま相対性理論でも変わらずに通用することが判明した。 というわけで、歴史的にはMaxwellの電磁気学は結果的にNewton力学に反例を与えることになった。それは何故だろう? 電磁気学でも微分積分だ出てくるのは、電界や磁界とかの座標を変数としてベクトルを与える関数を議論するからである。Newton力学の場合はすべての物理量(速度、加速度、力)は時間という一変数の関数だったが、電磁気学では静電場や静磁場は座標の関数であり、動電場や動磁場は時間と座標の関数でもある。すなわち扱う物理量がことごとく多変数関数であるということである。 電磁気学と同様に流体力学も座標の関数として速度や密度、圧力という物理量を数学的な対象として扱う。どちらかというと両者は近い関係にある。Maxwellも電磁気学に手を染める前は流体力学を研究してきた。そこで培った独自の自分数学がやがて電磁気学の定式化に役立つことになる。それでもHamiltonの弟子であるKateの助言に沿って四元数を元に定式化を試みたが、結果的には座標の成分毎に式を立てるという極めて見通しの悪い定式化になってしまった(初版の話)。 それを19世紀に最新のベクトル解析を使用して再構成したのがHeavisideでありHelzであった。それまでMaxwellの本を読んで難解なために読むのを躊躇していた学者達の多くはHelzの論文を読んで目から鱗の体験をすることになる。 ベクトル解析誕生の黒歴史は以前に書いた通りで、すでにその結果はHamiltonの四元数の研究者によって得られていたものと同じであったが、四元数は面倒で難しくて使えない数学だったのに対して、ベクトル解析ははるかに実用的だった。四元数派からベクトル解析派に鞍替えした元四元数研究者も英国では多かったと聞く。 さて疑問にはまだ答えが出ていない。何故Maxwellの電磁気学を理解する上でベクトル解析が必要だったのだろうか? それにはベクトル解析の長所を理解する必要がある。 (2015/7/9) だいぶ時間が経ってしまったが、忘れていたわけではなく、通勤中にも目を通してなかった手元の電磁気学の入門書を読み始めたり、Newtonのprincipiaを眺めてみたりしていた。 あまり読んでなかった分厚い電磁気学の入門書で日本語で書かれたものは、どうも著者の蘊蓄は抱負で数式が少なく入門には向いているかなと思って購入したのだが、良く読んでみるとそれは違っていた。書かれた年代が小生の生まれた頃と近いし、こんな人が東大で教えていたのかと思うと、さぞかし学生さんは大変だったろうなと気の毒に思ったりもした。 理由としては前半がどうやら戦前戦中の電磁気学の教授方法の伝統に沿っているかららしい。というのも戦前戦中は枢軸国であったドイツからしか科学技術系の外国図書は入手できなかったので(それも海軍の潜水艦で運ぶしかなかった)自ずとドイツの電気力学を基礎としていたと思われる。 つまり前半の章がやたらと力学的な観点での議論が多く、力はもとより、仕事とかエネルギーとかいう量が定義もなく出てくる。これには閉口した。 これには理由があって、ドイツではMaxwellが電磁気学の著書を出す前に既にWilhelm Weberで電気力学理論体系を作り上げていて、MaxwellがFaradayの考えていた電磁気力の近接作用論に基づいた場の理論であるのに対して、WeberのそれはNewton力学に基づいた遠隔作用論の力学だったためだ。 今日ではWeberの理論は存在すら顧みられることはなく、電磁気学と言えばMaxwellという合い言葉に全てが覆い尽くされてしまったように見えるが、Maxwellの理論の完成に拍車を掛けたのはWeberとKohlrauschが共同で行ったWeber定数(実は光速の√2倍の定数)の測定実験結果がMaxwellの予想した光の速度に近い(といっても√2倍の違いがある)ことから即座にそれが光速だと確信させたことによる。 皮肉にもNewtonの遠隔作用論に基づいたWeberの電気力学が世界に先駆けて光の伝達速度が有限であるという矛盾を証明する種となってしまい、力の伝達速度は有限であるという近接作用論にMaxwellが正しいという根拠を与えてしまう結果となった。Weber自身は知ってか知らずか、その実験結果が自分の研究の前途に暗雲を生み出す以外の何者でもないと確信したのか、論文上ではその結果はたいした価値はないという結論に結んでいる。そのためこの業績は価値がないものとして忘れられてしまうことに。 なんの話だったっけ? ああ、ベクトル解析の利便性ね。 話をNewtonに戻すと、そもそもprincipia執筆のきっかけを作ったのはHalley彗星の観測と研究成果で有名なHalleyの熱心な勧めによる。彗星の軌道を予測するのに必要な理論的な体系を既に持っていたNewtonにそれを本にするようにと勧めたのだ。 しかしNewtonにはまだ未解決の問題があって、すぐには執筆しなかった。しかしどうにも問題が解決しないので、やむなくその問題に関しては未完成のまま執筆したわけである。 その問題とは月の軌道計算問題である。月の軌道が正確に予想できれば潮の満ち引きだけでなく、航海上の経度を知る上でも役立つはずだった。 しかしそれは頓挫した。月の運行には地球だけでなく太陽の重力も関係しているため、太陽と彗星、太陽と惑星というような二つの質点の問題ではなく、太陽と月と地球の3つの質点の問題となるため、所謂3体問題で後にPoincareが示したように特別な場合を除いては解析的には解けないからである。 さて話はどんどんベクトル解析から遠ざかる傾向にあるが、元に戻ろう。 Newtonは当時の一般の知識人よりも一歩先を行っていたのは確かであるが、それをそのまま本に書いても認めてもらえそうもないので、当時の知識人が受け入れられるようにユークリッド幾何学による証明とラテン語による記述という方法を用いた。 これは成功し、すぐにヨーロッパ全土に本が行き渡った。ラテン語で書かれていたのが幸いしたのだろう。当時は学識者はみんなラテン語ができたので。 かのWeberをGöttingenに招聘して一緒に電磁気や重力の統一理論を模索していたGaussも若い頃にNewtonのprincipiaを読んで力学を学んだらしいから、Weberと意気投合したのは当然であり、その影響力の広がりは予想外に広範囲に及んだのは確かである。 Newtonは質点の運動軌跡をユークリッド平面上の曲線としてそれを解析するために自分数学(微分と積分)を展開することになる。 実際のところNewtonはユークリッド平面とそれに直交する時間軸を頭の中で考えていたのではないかという節もあるが、それは考え過ぎかもしれない。 しかしユークリッド平面に直交する時間軸を考えるととたんに近代的な力学がそこに見えてくる。 Einsteinが大学で数学を学んだ時の教授がMinkowskiで彼は3次元実数空間と直交する時間軸を加えたMinkowski空間を提唱していた。時間軸は空間と直交しなければならないので、実数ではなく純虚数としている点でMinkowski空間は実4次元空間とは異なる。それと時間軸の座標を時間tで光が進む距離(ct)としている。 ということでNewtonはそれに先だって二次元実平面空間とそれに直交する時間軸を3次元Minkowski空間として考えていたと仮定して議論を続けることにしよう。 まあ、これはあれだ、近代の力学の入門書はすべからくNewtonがもしベクトル解析でprincipiaを書いたらこうなるという風に書かれているのと一緒である。 (2015/10/1) ううむ、4元時空間でベクトル解析と電磁気学を再構成するというアイデアは良かったのだが、その道のりは予想外に険しいもので、古典的な構成法すら理解していない者にとっては困難というべきもので、時期尚早すぎた感がある。 なのでこのテーマは一旦保留して古典理解の道に戻るとしよう。 もちろん聡明な読者の中には、それが十分可能な方もおられると思うのでそれを妨げるものでは決してない。 むしろ、古典的な構成法の理解だけに満足せずに、更に広い視点から再構成する試みは力試しになるし、それがより簡潔な構成法となれば誰もが評価する仕事であることは言うまでもない。 |
| (1) 2 » | |
| スレッド表示 | 新しいものから | 前のトピック | 次のトピック | トップ |
| 投稿するにはまず登録を | |

