| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2015-4-21 10:25 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
Re: 自分の数学を持つことの勧め 電磁気学のテキストではベクトル解析の数学的な知識があることが前提としているものがほとんどだ(19世紀末とかまだベクトル解析が一般的ではなかった時代に出版されたものを除く)。
ベクトル解析の上に構築されているかのように見えて、電磁気学を学んでいるのかベクトル解析を学んでいるのか分からなくなってくる。 いつも躓くのはベクトル解析の常識が登場して、それに基づいて電磁気学の理論が解説される時だ。 このため最初の章で躓いて次ぎの章までたどり着けない。これは私だけではないだろう。 さて今日躓いたのは、たぶん常識的なことなんだろうけど、以前にも書いた並行四辺形の面積に絡んだ記述。 斜交する2つのベクトルa,bが作る並行四辺形の面積は となることだ。 こんなことがすぐに解るやつは頭おかしい、と考えるのはそんなこともすぐに解らないやつは頭悪いと言われる種族であることは確かである。さて貴方はどっちだろう。 電磁気学だけではないが、数学というのはシームレスにつながってはいない。突然まったくかけ離れたところに話が飛んでいってしまってついていけない人は落伍者となる。 普通に並行四辺形の面積というと、底辺x高さというのが小学校で習った知識である。 底辺を水平に平行に置いて、それに隣り合う辺が傾いている図を想像すると、傾きの角度がθであれば、2つの異なる辺a,bの長さを|a|,|b|とすれば、平行四辺形の面積は となるのは以前にも書いた。 幾何学的に表すと。 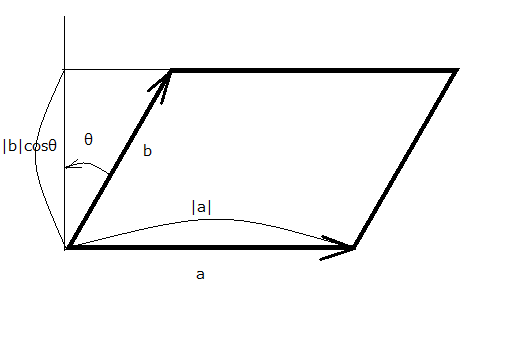 これと先の行列式で表された面積が等しいだなんてすぐには思いつかないし。 もちろん上の図で、ax=|a|, ay=0, bx=|b|sinθ, by=|b|cosθであるからして、行列式での面積の式と同値であることは確かである。 一般的な以下の並行四辺形ではどうだろうか? 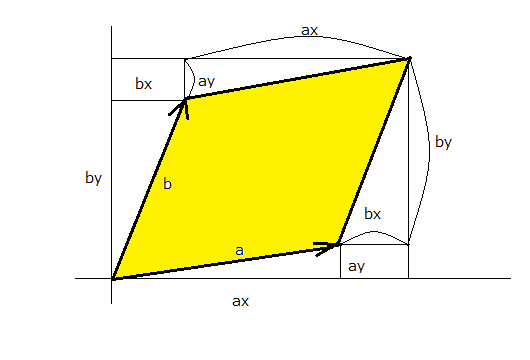 補助線をいくつも引いた結果から、黄色の平行四辺形の面積と対角的に接する一番大きな4角形の面積は 大きな四角形から問題の平行四辺形に含まれない余分な部分の面積は 従って黄色い並行四辺形の面積は、ベクトルa,bの成分で表すと ということでようやく理解できたことになる。 こんなの一瞬で解るほうが頭おかしい。 これ以外にも同じ結果の導出方法は沢山あると思われるが、それを確かめるのは読者の課題としよう(´∀` ) 実のところここはベクトル解析で基本中の基本の勘所な気がする。 P.S あとになって気付いたのは、積分の概念を知っていれば、もうひとつの見方で並行四辺形の面積が計算できるということ。 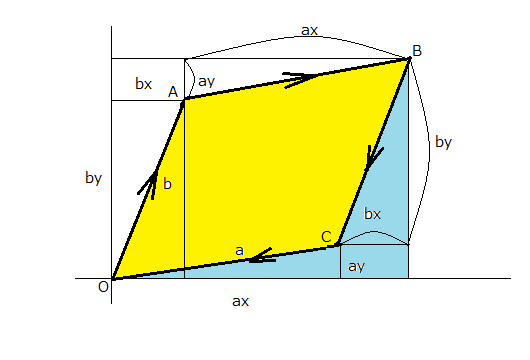 並行四辺形の外周の高さを並行四辺形の外周である閉路OABCOに沿って積分したものが平行四辺形の面積だと言える。 OABまではx座標が増加する方向にあるが、BCOは逆向きになるため積分結果の符号が変わる。 すなわちOABに渡って積分した値から、OCBに渡って積分した値を差し引けば並行四辺形の面積が得られるというわけである。 ということになる。 計算は面倒だが概念的にはこっちの方がすっきりする。 |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| |
webadm | 2015-2-3 12:47 |
| |
webadm | 2015-3-16 10:45 |
| |
webadm | 2015-3-17 9:57 |
| |
webadm | 2015-4-15 21:41 |
| » |
webadm | 2015-4-21 10:25 |
| |
webadm | 2015-4-26 21:43 |
| |
webadm | 2015-4-29 20:10 |
| |
webadm | 2015-5-5 5:33 |
| |
webadm | 2015-5-12 18:15 |
| |
webadm | 2015-5-20 9:56 |
| |
webadm | 2015-11-15 11:47 |
| |
webadm | 2015-12-19 21:03 |
| |
webadm | 2016-1-4 22:15 |
| |
webadm | 2016-1-10 22:07 |
| |
webadm | 2016-1-16 17:45 |
| |
webadm | 2016-4-6 12:47 |
| |
webadm | 2016-7-26 20:20 |
| 投稿するにはまず登録を | |

