| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2015-5-5 5:33 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
Re: 自分の数学を持つことの勧め 二次元平面上で斜交するベクトルa,bの張る平行四辺形の有効面積に正と負がある議論の続きをしよう。
以前に平行四辺形の面積が積分で考えることができると書いたが、それを使うと二つの面積が定義できる。 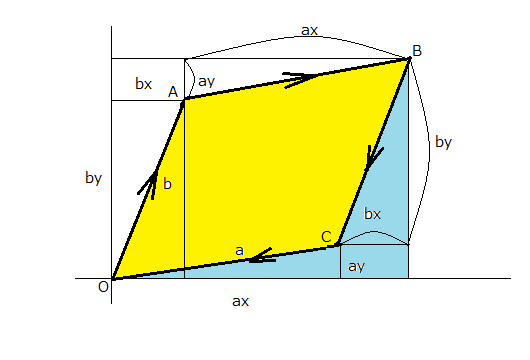 これともう一つが 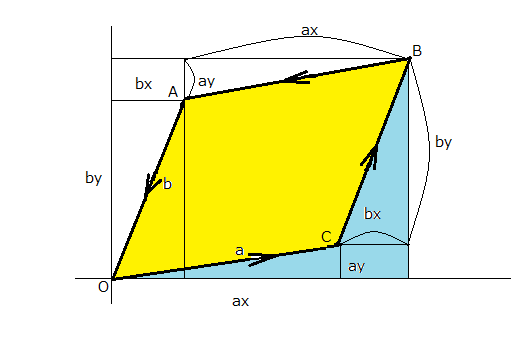 積分の方向を逆にしたので、互いに符号が異なるが絶対値は同じ平行四辺形の面積をとる。 これは当たり前の話である。 それではベクトルa,bを入れ替えた場合はどうなるだろう 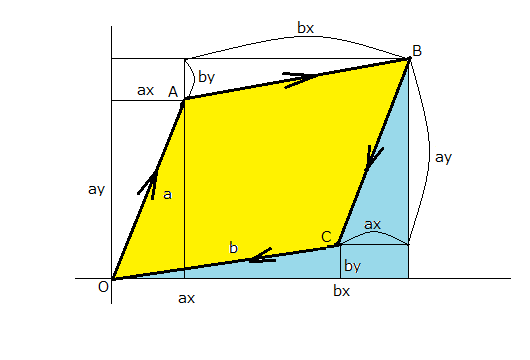 これは最初の面積のa,bを入れ替えたものだから面積は ということで絶対値は同じだがベクトルを入れ替える前と符号が異なる。 というわけで右回りと左周りの積分で符号が変わるのと、ベクトルを入れ替えると同じ方向の積分でも符号が変わるというのが確かめられる。 同じ原理を左手系に適用すると、話は逆になって右回りに積分すると負になり、左周りに積分しないと正の面積にならないことがわかる。 ところでこれはベクトルが張る象限の違いに影響するだろうかという疑問が沸いてくる。上の結果は第一象限については正しいが、他の象限や象限を跨いだ平行四辺形についても正しいのだろうか? それを確かめるにはベクトルを同じ角度だけ回転させても結果が変わらないかどうか確かめれば良い。 ベクトルをθだけ回転させる写像は以下の通りである これは以下の様に幾何学的に確かめることができる 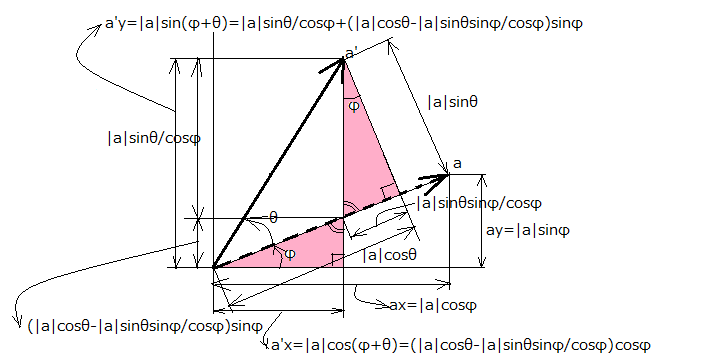 ということになる。 これは三角関数の加法定理そのものだけど、テキストで習う時にはそれは剥製で生きている対象ではないのですぐ忘れてしまいがちである。しかしベクトルの回転は生きた数学的な対象のまま目の前に存在するので、自分数学としては格好のターゲットである。 加法定理の公式を持ち出せば説明も要らないが、面白みもないし記憶にも残らなくなる。これならベクトルの回転と三角関数の加法定理がシームレスにつながっているので同時に理解できる。覚えやすいし、思い出し易い。というかこれ同じ事の言い換えじゃないのかという見方もできる。 さてこれで斜交する二つのベクトルa,bを任意の角度θだけ回転した場合に二つのベクトルが張る平行四辺形の面積がどうなるか計算してみればよい。 ということになる。 従って斜交する二つのベクトルが張る平行四辺形の有向面積は座標軸の回転に関して不変であることが確かめられた。 |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| |
webadm | 2015-2-3 12:47 |
| |
webadm | 2015-3-16 10:45 |
| |
webadm | 2015-3-17 9:57 |
| |
webadm | 2015-4-15 21:41 |
| |
webadm | 2015-4-21 10:25 |
| |
webadm | 2015-4-26 21:43 |
| |
webadm | 2015-4-29 20:10 |
| » |
webadm | 2015-5-5 5:33 |
| |
webadm | 2015-5-12 18:15 |
| |
webadm | 2015-5-20 9:56 |
| |
webadm | 2015-11-15 11:47 |
| |
webadm | 2015-12-19 21:03 |
| |
webadm | 2016-1-4 22:15 |
| |
webadm | 2016-1-10 22:07 |
| |
webadm | 2016-1-16 17:45 |
| |
webadm | 2016-4-6 12:47 |
| |
webadm | 2016-7-26 20:20 |
| 投稿するにはまず登録を | |

