| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2015-5-12 18:15 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
Re: 自分の数学を持つことの勧め さて二次元平面上の斜交するベクトルの積の結果は平べったい空間で正と負の向きを持つ有向面積というしっくり来ない結果をもたらすことは理解できたが、もうひとつ次元を増やした三次元空間上の任意の平面上の斜交する2つのベクトルの積を考えると、その真相がはっきりする。
簡単にするために三次元空間でx-y平面に平行で斜交する2つのベクトルの積を計算してみると 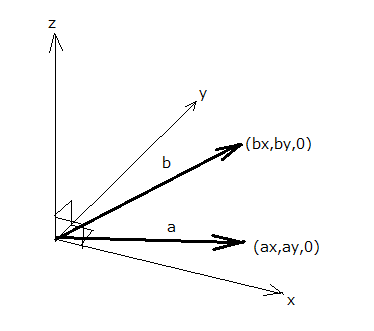 ということになる。 つまるところ三次元だと同一平面上の斜交するベクトルの積はベクトルが張る平行四辺形の有向面積の大きさを持つ平面に直交するもうひとつのベクトルを作り出すということになる。 二次元だと平べったい平面しか空間は存在しないので新たなベクトルを生成できないが、ベクトルの張る面積だけが定義できるという中途半端なことになる。 二次元と同様に上の関係式が成り立つもうひとつの三次元座標権が存在する。それは二次元の時と同様にちょうど鏡に映したような以下のような座標系である。 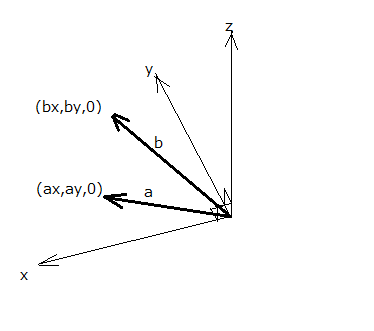 先の座標系は座標軸をどのように回転しても上の座標系とは一致しない。2つの座標軸は平行になっても、残りの座標軸の向きが反対になるのである。 しかし代数的には2つの座標系は同値であるから困ったことになる。 なので、前者をx軸を親指にy軸を人差し指として、中指をz軸に同じ向きになるようできるのは右手だけであるので右手系とし称して、逆に左手だけがそれが可能な後者の座標系は左手系と称する習わしになっている。 ベクトルの積がもうひとつのベクトルを生成する次元は限られていて、一次元と3次元と7次元だけであることが比較的簡単に証明できることが知られている。 ベクトルの積に関する局所的な議論はこのぐらいにしよう。 まだその先に躓きの石が待っている。 |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| |
webadm | 2015-2-3 12:47 |
| |
webadm | 2015-3-16 10:45 |
| |
webadm | 2015-3-17 9:57 |
| |
webadm | 2015-4-15 21:41 |
| |
webadm | 2015-4-21 10:25 |
| |
webadm | 2015-4-26 21:43 |
| |
webadm | 2015-4-29 20:10 |
| |
webadm | 2015-5-5 5:33 |
| » |
webadm | 2015-5-12 18:15 |
| |
webadm | 2015-5-20 9:56 |
| |
webadm | 2015-11-15 11:47 |
| |
webadm | 2015-12-19 21:03 |
| |
webadm | 2016-1-4 22:15 |
| |
webadm | 2016-1-10 22:07 |
| |
webadm | 2016-1-16 17:45 |
| |
webadm | 2016-4-6 12:47 |
| |
webadm | 2016-7-26 20:20 |
| 投稿するにはまず登録を | |

