| スレッド表示 | 古いものから | 前のトピック | 次のトピック | 下へ |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2009-10-15 19:22 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3097 |
複素角周波数 これまで交流回路の定常状態を解析するために用いてきたインピーダンスZ(jω)式中のjωを複素角周波数
s=σ+jω で置き換えた複素関数Z(s)を新たにインピーダンス関数と呼ぶ。 従って σ=0 と置くとそれは従来のインピーダンスZ(jω)の式と同じになるため、インピーダンス関数はインピーダンスをより一般化したものであると考えられる。 ωは角周波数でラジアン/秒の単位をもつ。従ってσも同様に時間当たりのなんらかの変化量を表すことになる。 複素角周波数の物理的な意味は、微分方程式の一般解が Kn*exp(sn*t) で表されることを考えると良く理解できる。 sn=σn+jωn であるので、展開すると Kn*exp(sn*t)=Kn*exp(σn)*exp(jωnt) =Kn*exp(σn*t)*(cos(ωnt)+j*sin(ωnt)) ということになる。これは実数部、虚数部どちらをとっても角周波数ωnの振動とσnによる時間領域での減衰(もしくは増大)を表している。 σn=0 なら Kn*(cos(ωnt)+j*sin(ωnt)) となり正弦波(虚数部)、もしくは余弦波(実数部)を表し 更に ωn=0 なら Kn となって直流を表すことになる。 従ってσとωの値の取り方の組み合わせによって、あらゆる応答を表すことが可能になる。 σ=0 & ω=0 : 時間にかかわらず一定の直流 σ>0 & ω=0 : 時間と共に絶対値が増大する直流 σ<0 & ω=0 : 時間と共に絶対値が減少する直流 σ=0 & ω≠0 : 時間にかかわらず振幅が一定の交流 σ>0 & ω≠0 : 時間と共に振幅が増大する交流 σ<0 & ω≠0 : 時間と共に振幅が現象する交流 これをグラフにプロットしてみると σ=0 & ω=0 wxplot2d([1], [x,0,100])$ 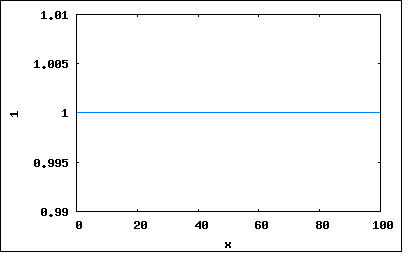 σ>0 & ω=0 wxplot2d([exp(0.04*x)*1], [x,0,100])$ 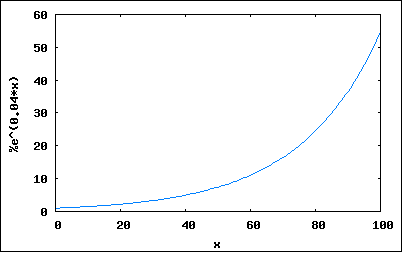 σ<0 & ω=0 wxplot2d([exp(-0.04*x)*1], [x,0,100])$ 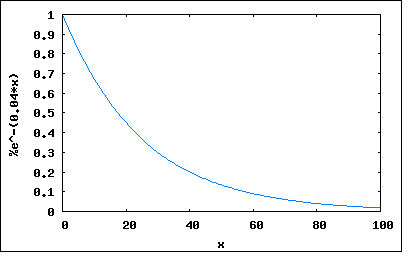 σ=0 & ω≠0 wxplot2d([cos(x)], [x,0,100])$ 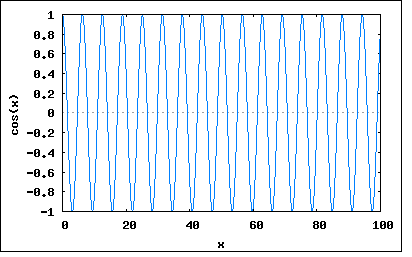 σ>0 & ω≠0 wxplot2d([exp(0.04*x)*cos(x)], [x,0,100])$ 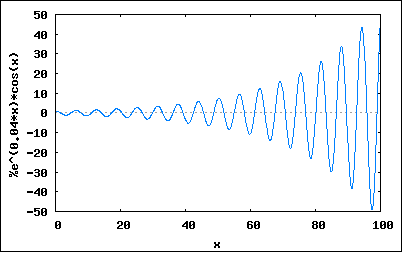 σ<0 & ω≠0 wxplot2d([exp(-0.04*x)*cos(x)], [x,0,100])$ 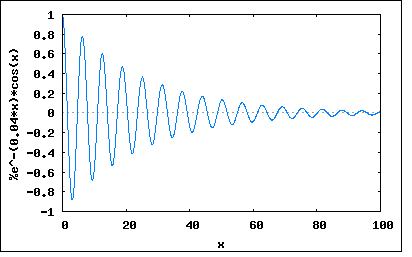 σをネーパー周波数、ωをラジアン周波数と名付けたのはW. H. Huggins。 I=I0*exp(σt) の自然対数を取ると σ=(1/t)ln(I/I0) ということになりσは毎秒当たりの比率の自然対数であることからネーパー(neper)周波数と名付けられた。 |
| webadm | 投稿日時: 2009-10-15 7:06 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3097 |
1端子対回路 下巻の第一章は一端子対回路。
回路網理論の延長上にあるが、ほとんどの電気回路理論の参考書や教科書では割愛されているインピーダンス関数やBruneの定理、リアクタンス関数、逆回路、定抵抗回路などの回路網解析理論を紹介している。 電気学会編の図書とかではこれらは割愛されて4端子(2端子対)回路だけで回路網理論はお終いなのが普通。ここにも著者のこだわりが感じられる。回路解析だけでなく、設計につきものの回路合成を行う場合には知っていないと損である。 後に学ぶことになる過渡解析やラプラス変換で使用される複素周波数が用いられるので、複素解析に関する数学知識が前提になるのも割愛される理由かもしれない。Riemann面とか出てくるものもあるし。 |
| « 1 (2) | |
| スレッド表示 | 古いものから | 前のトピック | 次のトピック | トップ |
| 投稿するにはまず登録を | |

