Gan's blog - フォーラム

« 1 (2) 3 4 »

投稿者	スレッド
webadm	投稿日時: 2010-4-15 9:49
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【10】インピーダンス関数とその回路ふう、やっと正実関数が終わった。次は与えられた零点と極を持つインピーダンス関数と回路を導けというもの。ただしいずれも周波数0におけるインピーダンス値がR[Ω]とする。 (1)零点を-b、極を-aに持つ駆動点インピーダンス関数は以下の様な形となるはずである $\begin{eqnarray}Z(s)&=&H\frac{\left(s+b\right)}{\left(s+a\right)}\end{eqnarray}$ 題意よりω=0では定抵抗回路になるのでスケーリングファクターHは $\begin{eqnarray}\left.Z(s)\right\|_{s=0}&=&\left.H\frac{\left(s+b\right)}{\left(s+a\right)}\right\|_{s=0}\\&=&H\frac{b}{a}\\&=&R\\H&=&\frac{Ra}{b}\end{eqnarray}$ ということになる。したがって駆動点インピーダンス関数は $\begin{eqnarray}Z(s)&=&\frac{Ra\left(s+b\right)}{b\left(s+a\right)}\end{eqnarray}$ ということになる。回路を合成するために展開すると $\begin{eq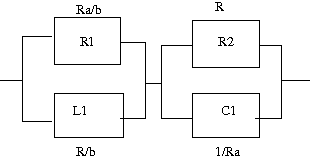narray}Z(s)&=&\frac{Ra\left(s+b\right)}{b\left(s+a\right)}\\&=&\frac{Ras}{bs+ab}+\frac{Rab}{bs+ab}\\&=&\frac{1}{\frac{1}{\Large\frac{b}{Ra}+\frac{b}{Rs}}}+\frac{1}{\Large\frac{s}{Ra}+\frac{1}{R}}\\&=&\frac{1}{\frac{1}{R_1}+\frac{1}{L_1 s}}+\frac{1}{C_1 s+\frac{1}{R_2}}\\R_1&=&\frac{Ra}{b}\,[\Omega]\\L_1&=&\frac{R}{b}\,[H]\\C_1&=&\frac{1}{R a}\,[F]\\R_2&=&R\,[\Omega]\end{eqnarray}$ 回路図を描くとということになる。著者の解答はa＞bという条件付きで誘導性インピーダンスを持つ回路となっているのに対して、こちらのはそういった制約の無い形である点が違う。元々a＞bという制約は題意には無いので、a=bやa＜bであってもよいはずだ。a=bの場合には零点と極は相殺されて消滅するので定抵抗Rとなる。a＜bの場合には、容量性インピーダンスということになる。誘導性か容量性のどちらかに決め打ちした場合には回路素子数はひとつ少なくすることができる。 (2)零点が-2a、極を-a±jbに持つ零点は実軸上で極は左半面に複素共役対で持つ。これも典型的な駆動点インピーダンス関数で表すと $\begin{eqnarray}Z(s)&=&H\frac{\left(s+2a\right)}{\left(s+a+jb\right)\left(s+a-jb\right)}\end{eqnarray}$ スケールファクタは $\begin{eqnarray}\left.Z(s)\right\|_{s=0}&=&\left.H\frac{\left(s+2a\right)}{\left(s+a+jb\right)\left(s+a-jb\right)}\right\|_{s=0}\\&=&H\frac{2a}{a^2+b^2}\\&=&R\\H&=&R\frac{a^2+b^2}{2a}\end{eqnarray}$ したがって駆動点インピーダンス関数は $\begin{eqnarray}Z(s)&=&R\frac{\left(a^2+b^2\right)\left(s+2a\right)}{2a\left(s+a+jb\right)\left(s+a-jb\right)}\end{eqnarray}$ ということになる。展開すると $begin{eqnarray}Z(s)&=&R\frac{\left(a^2+b^2\right)\left(s+2a\right)}{2a\left(s+a+jb\right)\left(s+a-jb\right)}\\&=&R\frac{\left(a^2+b^2\right)\left(s+2a\right)}{2a\left(s^2+2as+a^2+b^2\right)}\\&=&R\frac{\left(a^2+b^2\right)\left(s+2a\right)}{2a\left(s\left(s+2a\right)+a^2+b^2\right)}\\&=&\frac{1}{\frac{2a}{R\left(a^2+b^2\right)}s+\frac{2a}{R\left(s+2a\right)}}\\&=&\frac{1}{C_1 s+\frac{1}{L_1 s+R_1}}\\C_1&=&\frac{2a}{R\left(a^2+b^2\right)}\,[F]\\L_1&=&\frac{R}{2a}\,[H]\\R_1&=&R\,[\Omega]\end{eqnarray}$ ということになる。回路図で表すと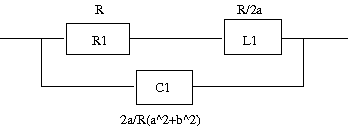ということになる。最後のは分母の式を分子の式と同じ共通項をくくりだすのがみそ。そうしないと展開結果がややこしいことになること請け合い。

webadm	投稿日時: 2010-4-15 17:02
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【11】リアクタンス回路次はリアクタンス回路に関する問題。どのようなリアクタンス回路のリアクタンスも周波数の増加とともに増大することを示せというもの。またサセプタンスについても。リアクタンス回路は損失を伴わないインダクタンスとキャパシタンスのみからなる回路で駆動点インピーダンスはリアクタンス関数で表される。したがってリアクタンス関数の値は零点を除いて純虚数となる。ここで問題とされるリアクタンスは、インピーダンスの虚数部を指している。これは理論の際にやったリアクタンス関数の虚軸上の微係数が常に正であるという証明問題と同じである。 $\begin{eqnarray}\left.\frac{dZ(s)}{ds}\right\|_{s=j\omega}&=&\left.\frac{d}{ds}(\frac{h_0}{s})+\frac{d}{ds}(\sum_{k=1}^n\frac{h_{2k}s}{s^2+{\omega_{2k}}^2})+\frac{d}{ds}(h_\infty{s})\right\|_{s=j\omega}\\&=&\left.-\frac{h_0}{s^2}+\sum_{k=1}^n(\frac{h_{2k}}{s^2+{\omega_{2k}}^2}-\frac{2h_{2k}s^2}{(s^2+{\omega_{2k}}^2)^2})+h_\infty\right\|_{s=j\omega}\\&=&\left.-\frac{h_0}{s^2}+\sum_{k=1}^n\frac{h_{2k}(s^2+{\omega_{2k}}^2)-2h_{2k}s^2}{(s^2+{\omega_{2k}}^2)^2}+h_\infty\right\|_{s=j\omega}\\&=&\left.-\frac{h_0}{s^2}+\sum_{k=1}^n\frac{{\omega_{2k}}^2-s^2}{(s^2+{\omega_{2k}}^2)^2}h_{2k}+h_\infty\right\|_{s=j\omega}\\&=&\frac{h_0}{\omega^2}+\sum_{k=1}^n\frac{{\omega_{2k}}^2+\omega^2}{({\omega_{2k}}^2-\omega^2)^2}h_{2k}+h_\infty\,\ge\,0\,\forall\omega\end{eqnarray}$ ということになる。先にs=jωを代入してωで微分すると、虚数単位(j)がかかった純虚数の微係数になってしまっていささか都合が悪い。純虚数にも大小があるとすれば同じことであるが。

webadm	投稿日時: 2010-4-15 19:39
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【12】続：リアクタンス回路次もリアクタンス回路。回路図で与えられたリアクタンス回路の共振及び反共振周波数を求め、その周波数特性の略図より零点と極が交互に並ぶことを示せというもの。共振点は零点、反共振点は極に対応するので、それらが決まるとリアクタンス関数が決まる。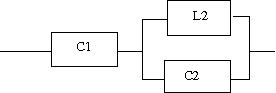回路図から駆動点インピーダンスの式を起こすと $\begin{eqnarray}Z(s)&=&\frac{1}{C_1 s}+\frac{1}{\frac{1}{L_2 s}+C_2 s}\\&=&\frac{1}{C_1 s}+\frac{L_2 s}{1+L_2 C_2 s^2}\\&=&\frac{L_2\left(C_1+C_2\right) s^2+1}{C_1 s\left(L_2 C_2 s^2+1\right)}\\&=&\left(\frac{C_1+C_2}{C_1 C_2}\right)\frac{\left(s^2+\frac{1}{L_2\left(C_1+C_2\right)}\right)}{s\left(s^2+\frac{1}{L_2 C_2}\right)}\\&=&H\frac{\left(s^2+{\omega_1}^2\right)}{s\left(s^2+{\omega_2}^2\right)}\\H&=&\frac{C_1+C_2}{C_1 C_2}\\\omega_1&=&\frac{1}{\sqrt{L_2\left(C_1+C_2\right)}}\\\omega_2&=&\frac{1}{\sqrt{L_2 C_2}}\end{eqnarray}$ このリアクタンス関数は零点（共振点）をω=ω1,∞、極（反共振点）をω=0,ω2に持つというのがわかる。また0＜ω1＜ω2＜∞という関係が成り立つので零点と極が交互に現れることを示している。リアクタンス値をプロットしてみよう。零点は1で極は2としている。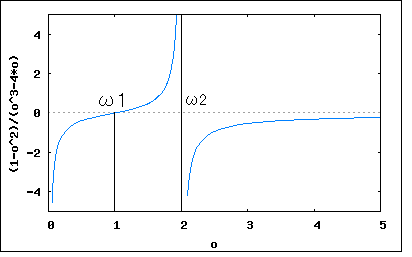回路図から駆動点インピーダンスの式を起こすと $\begin{eqnarray}Z(s)&=&\frac{1}{\frac{1}{\frac{1}{C_1 s}+L_1 s}+\frac{1}{\frac{1}{C_2 s}+L_2 s}}\\&=&\frac{1}{\frac{C_1 s}{1+C_1 L_1 s^2}+\frac{C_2 s}{1+C_2 L_2 s^2}}\\&=&\frac{\left(1+C_1 L_1 s^2\right)\left(1+C_2 L_2 s^2\right)}{C_1 s\left(1+C_2 L_2 s^2\right)+C_2 s\left(1+C_1 L_1 s^2\right)}\\&=&\left(\frac{L_1 L_2}{L_1+L_2}\right)\frac{\left(s^2+\frac{1}{C_1 L_1}\right)\left(s^2+\frac{1}{C_2 L_2}\right)}{s\left(s^2+\frac{C_1+C_2}{C_1 C_2\left(L_1+L_2\right)}\right)}\\&=&H\frac{\left(s^2+{\omega_1}^2\right)\left(s^2+{\omega_3}^2\right)}{s\left(s^2+{\omega_2}^2\right)}\\H&=&\frac{L_1 L_2}{L_1+L_2}\\\omega_1&=&\frac{1}{\sqrt{C_1 L_1}}\\\omega_2&=&\sqrt{\frac{C_1+C_2}{C_1 C_2\left(L_1+L_2\right)}}=\frac{1}{\sqrt{\left(\frac{C_1 C_2}{C_1+C_2}\right)\left(L_1+L_2\right)}}\\\omega_3&=&\frac{1}{\sqrt{C_2 L_2}}\end{eqnarray}$ 従って零点はω=ω1,ω3、極はω=0,ω2,∞ということになる。 0＜C2L2＜C1L2＜∞とすれば 0＜ω1＜ω2＜ω3＜∞という関係が成り立つので零点と極は交互に現れることが明らか。 ω1=1/2,ω2=1/√2,ω3=1とした場合の周波数特性をプロットすると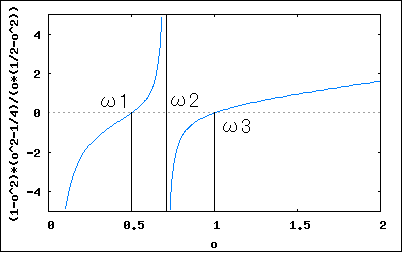ということになる。回路図から駆動点インピーダンスの式を起こすと $\begin{eqnarray}Z(s)&=&\frac{1}{C_1 s}+\frac{1}{C_2 s}+\frac{1}{\frac{1}{L_1 s}+\frac{1}{L_2 s}}\\&=&\frac{C_1+C_2}{C_1 C_2 s}+\frac{L_1 L_2 s}{L_1+L_2}\\&=&\frac{\left(C_1+C_2\right)\left(L_1+L_2\right)+C_1 C_2 L_1 L_2 s^2}{C_1 C_2\left(L_1+L_2\right)s}\\&=&\left(\frac{L_1 L_2}{L_1+L_2}\right)\frac{\left(s^2+\frac{\left(C_1+C_2\right)\left(L_1+L_2\right)}{C_1 C_2 L_1 L_2}\right)}{s}\\&=&H\frac{\left(s^2+{\omega_1}^2\right)}{s}\\H&=&\frac{L_1 L_2}{L_1+L_2}\\\omega_1&=&\sqrt{\frac{\left(C_1+C_2\right)\left(L_1+L_2\right)}{C_1 C_2 L_1 L_2}}=\frac{1}{\sqrt{\left(\frac{C_1 C_2}{C_1+C_2}\right)\left(\frac{L_1 L_2}{L_1+L_2}\right)}}\end{eqnarray}$ 回路図から予想が付くように、C1とC2の直列合成キャパシタンスとL1とL2の並列合成インダクタンスから成るLC直列回路と等価である。零点はω=ω1、極はω=0,∞に持つ。 C1,C2,L1,L2がそれぞれ0でなく有限値とすれば 0＜ω1＜∞なる関係が成り立つので零点と極は交互に現れる。周波数特性をω1=1としてプロットしてみると。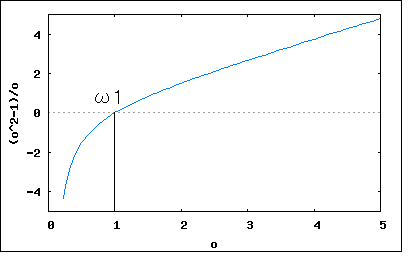ということになる。 P.S 設問２の 0＜ω1＜ω2＜ω3＜∞ が成り立つ証明は簡単なので読者の課題としよう(´∀` ) とどのつまり以下の不等式 $\begin{eqnarray}0\lt\frac{1}{\sqrt{C_1 L_1}}\lt\frac{1}{\sqrt{\left(\frac{C_1 C_2}{C_1+C_2}\right)\left(L_1+L_2\right)}}\lt\frac{1}{\sqrt{C_2 L_2}}\lt\infty\end{eqnarray}$ が0＜C2L2＜C1L2＜∞の条件下で成り立つことを証明すればよいわけである。

webadm	投稿日時: 2010-4-17 22:57
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【13】リアクタンス関数次ぎはリアクタンス関数に関する問題。以下の関数はリアクタンス関数かどうかというもの。 $\frac{s^2+3}{3s\left(s^2+2\right)\left(s^2+4\right)}$ リアクタンス関数の形式に書き直すと $\begin{eqnarray}Z(s)&=&H\frac{s^2+{\omega_1}^2}{s\left(s^2+{\omega_2}^2\right)\left(s^2+{\omega_4}^2\right)}\\H&=&\frac{1}{3}\\\omega_1&=&\sqrt{3}\\\omega_2&=&\sqrt{2}\\\omega_4&=&2\end{eqnarray}$ 零点はω1と∞、極は0,ω2,ω4ということになる。 0＜ω2＜ω1＜ω4＜∞ ということで零点と極が交互に並んでいないのでリアクタンス関数ではない。 Maximaで部分分数展開してみると $\frac{{s}^{2}+3}{3\,s\,\left({s}^{2}+2\right) \,\left( {s}^{2}+4\right) }=-\frac{s}{24\,\left( {s}^{2}+4\right) }-\frac{s}{12\,\left( {s}^{2}+2\right) }+\frac{1}{8\,s}$ 負の留数を持つので正実関数でもないということになる。よく見れば分子と分母の次数の差が2以上ある。この時点で正実関数ではない。

webadm	投稿日時: 2010-4-17 23:35
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【14】相互インダクタンスを含むリアクタンス回路次ぎは理論の時には出てこなかった相互インダクタンスを伴うリアクタンス回路に関する問題。以下の回路の共振点と反共振点を求めよというもの。ただしL1,L2>M^2とする。相互インダクタンスを伴う等価回路に書き直すとということになる。上記の回路から駆動点インピーダンス関数の式を起こすと $\begin{eqnarray}Z(s)&=&\left(L_1-M\right)s+\frac{1}{\frac{1}{\left(L_2-M\right)s+\frac{1}{C s}}+\frac{1}{M s}}\\&=&\left(L_1-M\right)s+\frac{1}{\frac{C s}{C\left(L_2-M\right)s^2+1}+\frac{1}{M s}}\\&=&\left(L_1-M\right)s+\frac{M s\left(C\left(L_2-M\right)s^2+1\right)}{\cancel{C M s^2}+C\left(L_2-\cancel{M}\right)s^2+1}\\&=&\frac{\left(C L_2 s^2+1\right)\left(L_1-M\right)s+M s\left(C\left(L_2-M\right)s^2+1\right)}{C L_2 s^2+1}\\&=&\frac{s\left(\left(C L_2 s^2+1\right)\left(L_1-M\right)+M \left(C\left(L_2-M\right)s^2+1\right)\right)}{C L_2 s^2+1}\\&=&\frac{s\left(C L_1 L_2 s^2+L_1-\cancel{M C L_2 s^2}-\cancel{M}+\cancel{M C L_2 s^2}-M^2 C s^2+\cancel{M}\right)}{C L_2 s^2+1}\\&=&\frac{s\left(C \left(L_1 L_2-M^2\right) s^2+L_1\right)}{C L_2 s^2+1}\\&=&\left(\frac{L_1 L_2-M^2}{L_2}\right)\frac{s\left( s^2+\frac{L_1}{C \left(L_1 L_2-M^2\right)}\right)}{ \left(s^2+\frac{1}{C L_2}\right)}\\&=&H\frac{s\left(s^2+{\omega_3}^2\right)}{\left(s^2+{\omega_2}^2\right)}\\H&=&\frac{L_1 L_2-M^2}{L_2}\\\omega_2&=&\frac{1}{\sqrt{C L_2}}\\\omega_3&=&\sqrt{\frac{L_1}{C \left(L_1 L_2-M^2\right)}}=\frac{1}{\sqrt{C\left(\frac{L_1 L_2-M^2}{L_1}\right)}\end{eqnarray}$ 従って零点（共振点）にω=0,ω3、極（反共振点）にω=ω2、∞を持つということになる。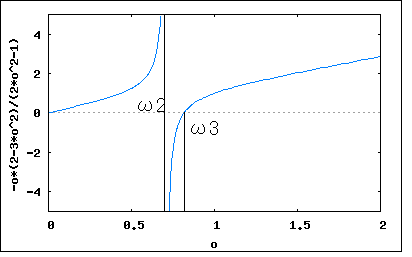

webadm	投稿日時: 2010-4-18 0:34
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【15】続々：リアクタンス回路次ぎはリアクタンス回路の計算問題。以下の回路のリアクタンスとアドミッタンスを求めよというもの。回路図から駆動点インピーダンス関数の式を起こすと $\begin{eqnarray}<br />Z(s)&=&\frac{1}{\Large C_1 s+\frac{1}{\frac{1}{C_2 s}+L_1 s}+\frac{1}{L_2 s}}\\<br />&=&\frac{1}{\Large\frac{C_1 L_2 s^2+1}{L_2 s}+\frac{C_2 s}{C_2 L_1 s^2+1}}\\<br />&=&\frac{L_2 s\left(C_2 L_1 s^2+1\right)}{\left(C_1 L_2 s^2+1\right)\left(C_2 L_1 s^2+1\right)+C_2 L_2 s^2}\\<br />&=&\frac{L_2 s\left(C_2 L_1 s^2+1\right)}{C_1 C_2 L_1 L_2 s^4+\left(C_1 L_2 +C_2 L_1+C_2 L_2\right)s^2+1}\\<br />&=&\left(\frac{1}{C_1}\right)\frac{s\left(s^2+\frac{1}{C_2 L_1}\right)}{\left(s^4+\frac{C_1 L_2 +C_2 L_1+C_2 L_2}{C_1 C_2 L_1 L_2}s^2+\frac{1}{C_1 C_2 L_1 L_2}\right)}<br />\end{eqnarray}$ 従ってリアクタンスはインピーダンスの虚数部なので $\begin{eqnarray}<br />X(\omega)&=&Im(Z(j\omega))\\<br />&=&Im(\left(\frac{1}{C_1}\right)\frac{j\omega\left(-\omega^2+\frac{1}{C_2 L_1}\right)}{\left(\omega^4-\frac{C_1 L_2 +C_2 L_1+C_2 L_2}{C_1 C_2 L_1 L_2}\omega^2+\frac{1}{C_1 C_2 L_1 L_2}\right)})\\<br />&=&\left(\frac{1}{C_1}\right)\frac{\omega\left(\frac{1}{C_2 L_1}-\omega^2\right)}{\left(\omega^4-\frac{C_1 L_2 +C_2 L_1+C_2 L_2}{C_1 C_2 L_1 L_2}\omega^2+\frac{1}{C_1 C_2 L_1 L_2}\right)}<br />\end{eqnarray}$ で表され。それぞれの素子定数を代入すると $\begin{eqnarray}<br />X(\omega)&=&\frac{\omega\left(25-\omega^2\right)}{\left(\omega^4-26.58\omega^2+8.33\right)}<br />\end{eqnarray}$ 分母の式は更に因数分解可能だが式が複雑になるのでそのままにしている。アドミッタンスはインピーダンスの逆数なので $\begin{eqnarray}<br />Y(j\omega)&=&\frac{1}{Z(j\omega)}\\<br />&=&C_1\frac{\left(\omega^4-\frac{C_1 L_2 +C_2 L_1+C_2 L_2}{C_1 C_2 L_1 L_2}\omega^2+\frac{1}{C_1 C_2 L_1 L_2}\right)}{j\omega\left(-\omega^2+\frac{1}{C_2 L_1}\right)}\\&=&jC_1\frac{\left(\omega^4-\frac{C_1 L_2 +C_2 L_1+C_2 L_2}{C_1 C_2 L_1 L_2}\omega^2+\frac{1}{C_1 C_2 L_1 L_2}\right)}{\omega\left(\omega^2-\frac{1}{C_2 L_1}\right)}\\<br />&=&j\frac{\left(\omega^4-26.58\omega^2+8.33\right)}{\omega\left(\omega^2-25\right)}<br />\end{eqnarray}$ この回路のリアクタンスをプロットしてみると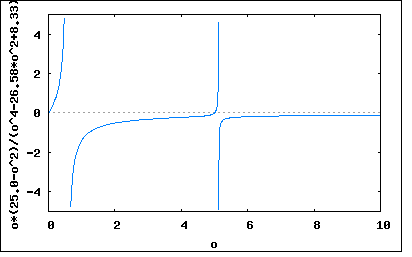アドミッタンスはちょうど零点と極が逆になった形になる。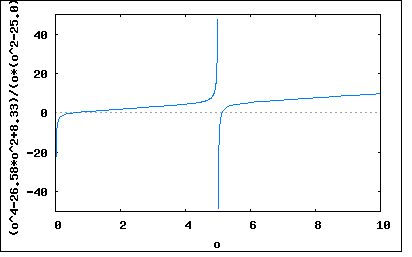回路図から駆動点インピーダンス関数の式を起こすと $\begin{eqnarray}<br />Z(s)&=&\frac{1}{\Large\frac{1}{\frac{1}{C_1 s}+L_1 s}+\frac{1}{\frac{1}{C_2 s}+L_2 s}+\frac{1}{L_3 s}}\\<br />&=&\frac{1}{\Large\frac{C_1 s}{1+C_1 L_1 s^2}+\frac{C_2 s}{1+C_2 L_2 s^2}+\frac{1}{L_3 s}}\\<br />&=&\frac{L_3 s\left(1+C_1 L_1 s^2\right)\left(1+C_2 L_2 s^2\right)}{C_1 L_3 s^2\left(1+C_2 L_2 s^2\right)+C_2 L_3 s^2\left(1+C_1 L_1 s^2\right)+\left(1+C_1 L_1 s^2\right)\left(1+C_2 L_2 s^2\right)}\\<br />&=&\frac{L_3 s\left(1+C_1 L_1 s^2\right)\left(1+C_2 L_2 s^2\right)}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)s^4+\left(C_1 L_3+C_2 L_3+C_1 L_1+C_2 L_2\right)s^2+1}\\<br />&=&\left(\frac{L_1 L_2 L_3}{L_2 L_3+L_1 L_3+L_1 L_2}\right)\frac{s\left(s^2+\frac{1}{C_1 L_1}\right)\left(s^2+\frac{1}{C_2 L_2}\right)}{\left(s^4+\frac{C_1 L_3+C_2 L_3+C_1 L_1+C_2 L_2}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}s^2+\frac{1}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}\right)}<br />\end{eqnarray}$ 従ってリアクタンスはインピーダンスの虚数部なので $\begin{eqnarray}<br />X(\omega)&=&Im(Z(j\omega))\\<br />&=&Im(\left(\frac{L_1 L_2 L_3}{L_2 L_3+L_1 L_3+L_1 L_2}\right)\frac{j\omega\left(-{\omega}^2+\frac{1}{C_1 L_1}\right)\left(-{\omega}^2+\frac{1}{C_2 L_2}\right)}{\left({\omega}^4-\frac{C_1 L_3+C_2 L_3+C_1 L_1+C_2 L_2}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}{\omega}^2+\frac{1}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}\right)})\\<br />&=&\left(\frac{L_1 L_2 L_3}{L_2 L_3+L_1 L_3+L_1 L_2}\right)\frac{\omega\left(\frac{1}{C_1 L_1}-\omega^2\right)\left(\frac{1}{C_2 L_2}-\omega^2\right)}{\left(\omega^4-\frac{C_1 L_3+C_2 L_3+C_1 L_1+C_2 L_2}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}\omega^2+\frac{1}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}\right)}<br />\end{eqnarray}$ で表され。それぞれの素子定数を代入すると $\begin{eqnarray}<br />X(\omega)&=&0.11538\frac{\omega\left(66.667-\omega^2\right)\left(166.67-\omega^2\right)}{\left(\omega^4-153.85\omega^2+4273.5\right)}<br />\end{eqnarray}$ 分母の式は更に因数分解可能だが式が複雑になるのでそのままにしている。アドミッタンスはインピーダンスの逆数なので $\begin{eqnarray}<br />Y(j\omega)&=&\frac{1}{Z(j\omega)}\\<br />&=&\left(\frac{L_2 L_3+L_1 L_3+L_1 L_2}{L_1 L_2 L_3}\right)\frac{\left({\omega}^4-\frac{C_1 L_3+C_2 L_3+C_1 L_1+C_2 L_2}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}{\omega}^2+\frac{1}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}\right)}{j\omega\left(-{\omega}^2+\frac{1}{C_1 L_1}\right)\left(-{\omega}^2+\frac{1}{C_2 L_2}\right)}\\<br />&=&j8.6667\frac{\left(\omega^4-153.85\omega^2+4273.5\right)}{\omega\left(\omega^2-66.667\right)\left(166.67-\omega^2\right)}<br />\end{eqnarray}$ この回路のリアクタンスをプロットしてみると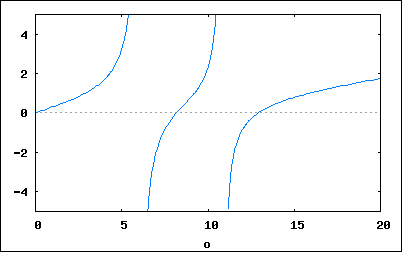アドミッタンスはちょうど零点と極が逆になった形になる。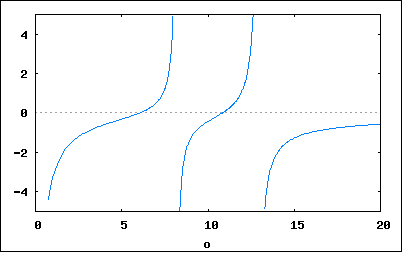

webadm	投稿日時: 2010-4-19 2:30
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【16】リアクタンス回路の合成次ぎはお待ちかね（誰も待ってないって）リアクタンス回路の合成問題。以下のリアクタンス関数からFoster展開とCauer展開でそれぞれ２種類ずつ回路を合成せよというもの。 $Z_1(s)=\frac{\left(s^2+1\right)\left(s^2+9\right)}{s\left(s^2+4\right)}$ Foster展開はインピーダンスの総和へ部分分数展開する形とアドミッタンスの総和へ部分分数展開する形の２種類に合成できる。まずはインピーダンスの総和に部分分数展開してみよう。 $\begin{eqnarray}<br />Z_1(s)&=&\frac{K_0}{s}+\frac{K_1 s}{s^2+4}+K_\infty s\\<br />&=&\frac{1}{C_0 s}+\frac{1}{C_1 s+\frac{1}{L_1 s}}+L_\infty s\\<br />C_0&=&\frac{1}{K_0}=\frac{4}{9}\,[F]\\<br />C_1&=&\frac{1}{K_1}=\frac{4}{15}\,[H]\\<br />L_1&=&\frac{K_1}{4}=\frac{15}{16}\,[H]\\<br />L_\infty&=&K_\infty=1\,[H]\\<br />K_0&=&\lim_{s^2\to0}sZ_1(s)=\left.\frac{\left(s^2+1\right)\left(s^2+9\right)}{\left(s^2+4\right)}\right\|_{s^2=0}\\<br />&=&\frac{9}{4}\\<br />K_1&=&\lim_{s^2\to-4}\frac{\left(s^2+4\right)Z_1(s)}{s}=\left.\frac{\left(s^2+1\right)\left(s^2+9\right)}{s^2}\right\|_{s^2=-4}\\<br />&=&\frac{\left(-4+1\right)\left(-4+9\right)}{-4}\\<br />&=&\frac{15}{4}\\<br />K_\infty&=&\lim_{s^2\to\infty}\frac{Z_1(s)}{s}=\left.\frac{\left(s^2+1\right)\left(s^2+9\right)}{s^2\left(s^2+4\right)}\right\|_{s^2=\infty}\\<br />&=&\left.\frac{\left(1+\frac{1}{s^2}\right)\left(1+\frac{9}{s^2}\right)}{\left(1+\frac{4}{s^2}\right)}\right\|_{s^2=\infty}\\<br />&=&1<br />\end{eqnarray}$ 回路図を描くと同様にアドミッタンスの総和へ部分分数展開すると $\begin{eqnarray}<br />Y_1(s)&=&\frac{1}{Z_1(s)}=\frac{s\left(s^2+4\right)}{\left(s^2+1\right)\left(s^2+9\right)}\\<br />&=&\frac{K_1 s}{s^2+1}+\frac{K_2 s}{s^2+9}\\<br />&=&\frac{1}{L_1 s+\frac{1}{C_1 s}}+\frac{1}{L_2 s+\frac{1}{C_2 s}}\\<br />L_1&=&\frac{1}{K_1}=\frac{8}{3}\,[H]\\<br />C_1&=&K_1=\frac{3}{8}\,[F]\\<br />L_2&=&\frac{1}{K_2}=\frac{8}{5}\,[H]\\<br />C_2&=&\frac{K_2}{9}=\frac{5}{72}\,[F]\\<br />K_1&=&\lim_{s^2\to-1}\frac{\left(s^2+1\right)Y_1(s)}{s}\\<br />&=&\left.\frac{s^2+4}{s^2+9}\right\|_{s^2=-1}\\<br />&=&\frac{-1+4}{-1+9}\\<br />&=&\frac{3}{8}\\<br />K_2&=&\lim_{s^2\to-9}\frac{\left(s^2+9\right)Y_1(s)}{s}\\<br />&=&\left.\frac{s^2+4}{s^2+1}\right\|_{s^2=-9}\\<br />&=&\frac{-9+4}{-9+1}\\<br />&=&\frac{5}{8}<br />\end{eqnarray}$ 回路図を描くと今度はCauer展開。Cauer展開は次数の最も大きな項から割り出すのと次数の最も小さい項から割り出す２通りの形がある。まず次数の大きな項から割り出してみよう。 $\begin{eqnarray}<br />Z_1(s)&=&\frac{\left(s^2+1\right)\left(s^2+9\right)}{s\left(s^2+4\right)}\\<br />&=&\frac{s^4+10s^2+9}{s^3+4s}\\<br />&=&s+\frac{6s^2+9}{s^3+4s}\\<br />&=&s+\frac{1}{\Large\frac{1}{6}s+\frac{\left(4-\frac{9}{6}\right)s}{6s^2+9}}\\<br />&=&s+\frac{1}{\Large\frac{1}{6}s+\frac{1}{\frac{12}{5}s+\frac{1}{\frac{5}{18}s}}}\\<br />&=&L_1 s+\frac{1}{\Large C_2 s+\frac{1}{L_3 s+\frac{1}{C_4 s}}}\\<br />L_1&=&1\,[H]\\<br />C_2&=&\frac{1}{6}\,[F]\\<br />L_3&=&\frac{12}{5}\,[H]\\<br />C_4&=&\frac{5}{18}\,[F]\\<br />\end{eqnarray}$ 回路図を描くと今度は次数の最も少ない項から割り出すと $\begin{eqnarray}<br />Z_1(s)&=&\frac{\left(s^2+1\right)\left(s^2+9\right)}{s\left(s^2+4\right)}\\<br />&=&\frac{s^4+10s^2+9}{s^3+4s}\\<br />&=&\frac{9p^4+10p^2+1}{4p^3+p}\\<br />&=&\frac{9}{4}p+\frac{\left(10-\frac{9}{4}\right)p^2+1}{4p^3+p}\\<br />&=&\frac{9}{4}p+\frac{1}{\Large\frac{16}{31}p+\frac{\left(1-\frac{16}{31}\right)p}{\frac{31}{4}p^2+1}}\\<br />&=&\frac{9}{4}p+\frac{1}{\Large\frac{16}{31}p+\frac{1}{\frac{961}{60}p+\frac{31}{15p}}}\\<br />&=&\frac{9}{4s}+\frac{1}{\Large\frac{16}{31s}+\frac{1}{\frac{961}{60s}+\frac{31}{15}s}}\\<br />&=&\frac{1}{C_1 s}+\frac{1}{\Large\frac{1}{L_2 s}+\frac{1}{\frac{1}{C_3 s}+L_4 s}}\\<br />C_1&=&\frac{4}{9}\,[F]\\<br />L_2&=&\frac{31}{16}\,[H]\\<br />C_3&=&\frac{60}{961}\,[F]\\<br />L_4&=&\frac{31}{15}\,[H]\\<br />p&=&s^{-1}<br />\end{eqnarray}$ 回路図を描くと $Z_2(s)=\frac{\left(s^2+2\right)\left(s^2+6\right)}{s\left(s^2+4\right)}$ インピーダンスの総和に部分分数展開してみよう。 $\begin{eqnarray}<br />Z_2(s)&=&\frac{\left(s^2+2\right)\left(s^2+6\right)}{s\left(s^2+4\right)}\\<br />&=&\frac{K_0}{s}+\frac{K_1 s}{s^2+4}+K_\infty s\\<br />&=&\frac{1}{C_0 s}+\frac{1}{C_1 s+\frac{1}{L_1 s}}+L_\infty s\\<br />C_0&=&\frac{1}{K_0}=\frac{1}{3}\,[F]\\<br />C_1&=&\frac{1}{K_1}=1\,[F]\\<br />L_1&=&\frac{K_1}{4}=\frac{1}{4}\,[H]\\<br />L_\infty&=&K_\infty=1\,[H]\\<br />K_0&=&\lim_{s^2\to0}sZ_2(s)=\left.\frac{\left(s^2+2\right)\left(s^2+6\right)}{\left(s^2+4\right)}\right\|_{s^2=0}\\<br />&=&3\\<br />K_1&=&\lim_{s^2\to-4}\frac{\left(s^2+4\right)Z_2(s)}{s}=\left.\frac{\left(s^2+2\right)\left(s^2+6\right)}{s^2}\right\|_{s^2=-4}\\<br />&=&\frac{\left(-4+2\right)\left(-4+6\right)}{-4}\\<br />&=&1\\<br />K_\infty&=&\lim_{s^2\to\infty}\frac{Z_2(s)}{s}=\left.\frac{\left(s^2+2\right)\left(s^2+6\right)}{s^2\left(s^2+4\right)}\right\|_{s^2=\infty}\\<br />&=&\left.\frac{\left(1+\frac{2}{s^2}\right)\left(1+\frac{6}{s^2}\right)}{1+\frac{4}{s^2}}\right\|_{s^2=\infty}\\<br />&=&1<br />\end{eqnarray}$ 回路図を描くと同様にアドミッタンスの総和へ部分分数展開すると $\begin{eqnarray}<br />Y_2(s)&=&\frac{1}{Z_2(s)}=\frac{s\left(s^2+4\right)}{\left(s^2+2\right)\left(s^2+6\right)}\\<br />&=&\frac{K_1 s}{s^2+2}+\frac{K_2 s}{s^2+6}\\<br />&=&\frac{1}{C_1 s+\frac{1}{L_1 s}}+\frac{1}{C_2 s+\frac{1}{L_2 s}}\\<br />C_1&=&\frac{1}{K_1}=2\,[F]\\<br />L_1&=&\frac{K_1}{2}=\frac{1}{4}\,[H]\\<br />C_2&=&\frac{1}{K_2}=2\,[F]\\<br />L_2&=&\frac{K_2}{6}=\frac{1}{12}\,[H]\\<br />K_1&=&\lim_{s^2\to-2}\frac{\left(s^2+2\right)Y_2(s)}{s}\\<br />&=&\left.\frac{s^2+4}{s^2+6}\right\|_{s^2=-2}\\<br />&=&\frac{-2+4}{-2+6}\\<br />&=&\frac{1}{2}\\<br />K_2&=&\lim_{s^2\to-6}\frac{\left(s^2+6\right)Y_2(s)}{s}\\<br />&=&\left.\frac{s^2+4}{s^2+2}\right\|_{s^2=-6}\\<br />&=&\frac{-6+4}{-6+2}\\<br />&=&\frac{1}{2}\\<br />\end{eqnarray}$ 回路図を描くと今度はCauer展開。まず次数の大きな項から割り出してみよう。 $\begin{eqnarray}<br />Z_1(s)&=&\frac{\left(s^2+2\right)\left(s^2+6\right)}{s\left(s^2+4\right)}\\<br />&=&\frac{s^4+8s^2+12}{s^3+4s}\\<br />&=&s+\frac{4s^2+12}{s^3+4s}\\<br />&=&s+\frac{1}{\Large\frac{1}{4}s+\frac{\left(4-\frac{12}{4}\right)s}{4s^2+12}}\\<br />&=&s+\frac{1}{\Large\frac{1}{4}s+\frac{1}{4s+\frac{12}{s}}}\\<br />&=&L_1 s+\frac{1}{\Large C_2 s+\frac{1}{L_3 s+\frac{1}{C_4 s}}}\\<br />L_1&=&1\,[H]\\<br />C_2&=&\frac{1}{4}\,[F]\\<br />L_3&=&4\,[H]\\<br />C_4&=&\frac{1}{12}\,[F]<br />\end{eqnarray}$ 回路図を描くと今度は次数の最も少ない項から割り出すと $\begin{eqnarray}<br />Z_1(s)&=&\frac{\left(s^2+2\right)\left(s^2+6\right)}{s\left(s^2+4\right)}\\<br />&=&\frac{s^4+8s^2+12}{s^3+4s}\\<br />&=&\frac{12p^4+8p^2+1}{4p^3+p}\\<br />&=&3p+\frac{5p^2+1}{4p^3+p}\\<br />&=&3p+\frac{1}{\Large\frac{4}{5}p+\frac{\left(1-\frac{4}{5}\right)p}{5p^2+1}}\\<br />&=&3p+\frac{1}{\Large\frac{4}{5}p+\frac{1}{25p+\frac{5}{p}}}\\<br />&=&\frac{3}{s}+\frac{1}{\Large\frac{4}{5s}+\frac{1}{\frac{25}{s}+5s}}\\<br />&=&\frac{1}{C_1 s}+\frac{1}{\Large\frac{1}{L_2 s}+\frac{1}{\frac{1}{C_3 s}+L_4 s}}\\<br />C_1&=&\frac{1}{3}\,[F]\\<br />L_2&=&\frac{5}{4}\,[H]\\<br />C_3&=&\frac{1}{25}\,[F]\\<br />L_4&=&5\,[H]\\<br />p&=&s^{-1}<br />\end{eqnarray}$ 回路図を描くと

webadm	投稿日時: 2010-4-19 10:09
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【17】続：リアクタンス回路の合成ここからしばらくリアクタンス回路の合成問題が続く。次ぎの問題は与えられた周波数特性を満足するリアクタンス一端子対回路を（１）並列共振回路の直列接続（第一Foster展開）（２）直列共振回路の並列接続（第二Foster展開）（３）はしご形かいろ（Cauer展開）で合成せよというもの。与えられる周波数特性は H(スケーリングファクタ）は0.2 共振角周波数ω1=1000[rad/sec]、ω3=3000[rad/sec] 反共振角周波数ω2=2000[rad/sec] とする。問題文にはスケーリングファクタの単位が[H]とか誤って記載されているが、スケーリングファクタは無次元なので単位などないので明らかに著者の誤記。周波数特性で重要となるω=0と∞が零点なのか極なのかが与えられていないが、与えられた零点と極の関係から 0＜ω1＜ω2＜ω3＜∞ となるので、リアクタンス関数は零点と極が交互に位置しているのでω1とω3が零点でω2が極であるのでω=0とω=∞は極であることは自明。となるとすべての特異点が明らかになり、スケーリングファクタも与えられているのでリアクタンス関数は以下の通りとなる。 $\begin{eqnarray}<br />Z(s)&=&H\frac{\left(s^2+{\omega_1}^2\right)\left(s^2+{\omega_3}^2\right)}{s\left(s^2+{\omega_2}^2\right)}\\<br />&=&0.2\frac{\left(s^2+1000^2\right)\left(s^2+3000^2\right)}{s\left(s^2+2000^2\right)}<br />\end{eqnarray}$ リアクタンス関数が定まれば回路合成が出来るので。第一Foster展開をすると $\begin{eqnarray}<br />Z(s)&=&0.2\frac{\left(s^2+1000^2\right)\left(s^2+3000^2\right)}{s\left(s^2+2000^2\right)}\\<br />&=&\frac{H_0}{s}+\frac{H_1 s}{s^2+2000^2}+H_\infty s\\<br />&=&\frac{1}{C_0 s}+\frac{1}{C_1 s+\frac{1}{L_1 s}}+L_\infty s\\<br />C_0&=&\frac{1}{H_0}=\frac{1}{450000}=2.22\,[\mu F]\\<br />C_1&=&\frac{1}{H_1}=\frac{1}{750000}=1.33\,[\mu H]\\<br />L_1&=&\frac{H_1}{2000^2}=\frac{750000}{2000^2}=187.5\,[mH]\\<br />L_\infty&=&H_\infty=0.2\,[H]\\<br />H_0&=&\lim_{s^2\to0}sZ(s)=\left.0.2\frac{\left(s^2+1000^2\right)\left(s^2+3000^2\right)}{\left(s^2+2000^2\right)}\right\|_{s^2=0}\\<br />&=&0.2\frac{\left(1000^2\right)\left(3000^2\right)}{\left(2000^2\right)}\\<br />&=&450000\\<br />H_1&=&\lim_{s^2\to-2000^2}\frac{\left(s^2+2000^2\right)Z(s)}{s}=\left.0.2\frac{\left(s^2+1000^2\right)\left(s^2+3000^2\right)}{s^2}\right\|_{s^2=-2000^2}\\<br />&=&0.2\frac{\left(-2000^2+1000^2\right)\left(-2000^2+3000^2\right)}{-2000^2}\\<br />&=&750000\\<br />H_\infty&=&\lim_{s^2\to\infty}\frac{Z(s)}{s}=\left.0.2\frac{\left(s^2+1000^2\right)\left(s^2+3000^2\right)}{s^2\left(s^2+2000^2\right)}\right\|_{s^2=\infty}\\<br />&=&\left.0.2\frac{\left(1+\frac{1000^2}{s^2}\right)\left(1+\frac{3000^2}{s^2}\right)}{\left(1+\frac{2000^2}{s^2}\right)}\right\|_{s^2=\infty}\\<br />&=&0.2<br />\end{eqnarray}$ 回路図で表すと次ぎに第二Foster展開はアドミッタンスの総和に部分分数展開すればよいので $\begin{eqnarray}<br />Y(s)&=&\frac{1}{Z(s)}=\frac{s\left(s^2+2000^2\right)}{0.2\left(s^2+1000^2\right)\left(s^2+3000^2\right)}\\<br />&=&\frac{H_1 s}{s^2+1000^2}+\frac{H_2 s}{s^2+3000^2}\\<br />&=&\frac{1}{L_1 s+\frac{1}{C_1 s}}+\frac{1}{L_2 s+\frac{1}{C_2 s}}\\<br />L_1&=&\frac{1}{H_1}=\frac{1}{1.875}=533.3\,[mH]\\<br />C_1&=&\frac{H_1}{1000^2}=\frac{1.875}{1000^2}=1.875\,[\mu F]\\<br />L_2&=&\frac{1}{H_2}=\frac{1}{3.125}=320\,[mH]\\<br />C_2&=&\frac{H_2}{3000^2}=\frac{3.125}{3000^2}=0.3472\,[\mu F]\\<br />H_1&=&\lim_{s^2\to-1000^2}\frac{\left(s^2+1000^2\right)Y(s)}{s}=\left.\frac{\left(s^2+2000^2\right)}{0.2\left(s^2+3000^2\right)}\right\|_{s^2=-1000^2}\\<br />&=&\frac{\left(-1000^2+2000^2\right)}{0.2\left(-1000^2+3000^2\right)}\\<br />&=&1.875\\<br />H_2&=&\lim_{s^2\to-3000^2}\frac{\left(s^2+3000^2\right)Y(s)}{s}=\left.\frac{\left(s^2+2000^2\right)}{0.2\left(s^2+1000^2\right)}\right\|_{s^2=-3000^2}\\<br />&=&\frac{\left(-3000^2+2000^2\right)}{0.2\left(-3000^2+1000^2\right)}\\<br />&=&3.125<br />\end{eqnarray}$ 回路図で表すと最後にCauer展開。へそ曲がりで別解の第二Cauer展開でやってみよう。 $\begin{eqnarray}<br />Z(s)&=&0.2\frac{\left(s^2+1000^2\right)\left(s^2+3000^2\right)}{s\left(s^2+2000^2\right)}\\<br />&=&\frac{0.2s^4+0.2\left(1000^2+3000^2\right)s^2+0.2\left(1000^2\right)\left(3000^2\right)}{s^3+200^2s}\\<br />&=&\frac{0.2\left(1000^2\right)\left(3000^2\right)p^4+0.2\left(1000^2+3000^2\right)p^2+0.2}{2000^2p^3+p}\\<br />&=&\frac{0.2\left(1000^2\right)\left(3000^2\right)}{2000^2}p+\frac{\left(0.2\left(1000^2+3000^2\right)-\frac{0.2\left(1000^2\right)\left(3000^2\right)}{2000^2}\right)p^2+0.2}{2000^2p^3+p}\\<br />&=&450000p+\frac{1550000p^2+0.2}{2000^2p^3+p}\\<br />&=&450000p+\frac{1}{\Large\frac{2000^2}{1550000}p+\frac{\left(1-0.2\frac{2000^2}{1550000}\right)p}{1550000p^2+0.2}}\\<br />&=&450000p+\frac{1}{\Large\frac{80}{31}p+\frac{\frac{15}{31}p}{1550000p^2+0.2}}\\<br />&=&\frac{450000}{s}+\frac{1}{\Large\frac{80}{31s}+\frac{1}{\frac{9610000}{3s}+\frac{31}{75}s}}\\<br />&=&\frac{1}{C_1 s}+\frac{1}{\Large\frac{1}{L_2 s}+\frac{1}{\frac{1}{C_3 s}+L_4 s}}\\<br />C_1&=&\frac{1}{450000}=2.22\,[\mu F]\\<br />L_2&=&\frac{31}{80}=387.5\,[mH]\\<br />C_3&=&\frac{3}{9610000}=0.3122\,[\mu F]\\<br />L_4&=&\frac{31}{75}=413.3\,[mH]\\<br />p&=&s^{-1}<br />\end{eqnarray}$ 回路図で表すと

webadm	投稿日時: 2010-4-20 4:22
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【18】続々：リアクタンス回路の合成次ぎは少しひねったリアクタンス回路の合成問題。極と零点と、スケーリングファクタの代わりに零点における微係数が与えられている点が前問と異なる。極は ω2=2000[rad/sec] ω4=4000[rad/sec] 零点は ω3=3000[rad/sec] 零点における微係数 dX/dω=4/7[Ω/rad/sec] というもの。 0＜ω2＜ω3＜ω4＜∞ なる関係から、他にω=0、∞に零点を持つことが明らか。従って以下の様なリアクタンス関数の形になるはず。 $Z(s)=H\frac{s\left(s^2+{\omega_3}^2\right)}{\left(s^2+{\omega_2}^2\right)\left(s^2+{\omega_4}^2\right)}$ スケーリングファクタHは $\begin{eqnarray}<br />\lim_{\omega\to\omega_3}\frac{dX(\omega)}{d\omega}&=&\lim_{\omega\to\omega_3}\frac{d}{d\omega}Im\left(Z(j\omega)\right)\\<br />&=&\lim_{\omega\to\omega_3}\frac{d}{d\omega}Im\left(H\frac{j\omega\left(-{\omega}^2+{\omega_3}^2\right)}{\left(-{\omega}^2+{\omega_2}^2\right)\left(-{\omega}^2+{\omega_4}^2\right)}\right)\\<br />&=&\lim_{\omega\to\omega_3}\frac{d}{d\omega}H\frac{\omega\left( {\omega_3}^{2}-{\omega}^{2}\right)}{\left( {\omega_2}^{2}-{\omega}^{2}\right) \,\left( {\omega_4}^{2}-{\omega}^{2}\right) }\\<br />&=&\left.H\left(\frac{\left( {\omega_3}^{2}-{\omega}^{2}\right)}{\left( {\omega_2}^{2}-{\omega}^{2}\right) \,\left( {\omega_4}^{2}-{\omega}^{2}\right) }+\frac{2\,{\omega}^{2}\,\left( {\omega_3}^{2}-{\omega}^{2}\right)}{{\left( {\omega_2}^{2}-{\omega}^{2}\right) }^{2}\,\left( {\omega_4}^{2}-{\omega}^{2}\right) }-\frac{2\,{\omega}^{2}}{\left( {\omega_2}^{2}-{\omega}^{2}\right) \,\left( {\omega_4}^{2}-{\omega}^{2}\right) }+\frac{2\,{\omega}^{2}\,\left( {\omega_3}^{2}-{\omega}^{2}\right)}{\left( {\omega_2}^{2}-{\omega}^{2}\right) \,{\left( {\omega_4}^{2}-{\omega}^{2}\right) }^{2}}\right)\right\|_{\omega=\omega_3}\\<br />&=&-H\frac{2\,{\omega_3}^{2}}{\left( {\omega_2}^{2}-{\omega_3}^{2}\right) \,\left( {\omega_4}^{2}-{\omega_3}^{2}\right) }\\<br />&=&-H\frac{2\cdot{3000}^{2}}{\left( {2000}^{2}-{3000}^{2}\right) \,\left( {4000}^{2}-{3000}^{2}\right) }\\<br />&=&H\frac{9}{17500000}\\<br />&=&\frac{4}{7}\\<br />H&=&\frac{10000000}{9}<br />\end{eqnarray}$ 従って最終的なリアクタンス関数は $Z(s)=\left(\frac{10000000}{9}\right)\frac{s\left(s^2+{\omega_3}^2\right)}{\left(s^2+{\omega_2}^2\right)\left(s^2+{\omega_4}^2\right)}$ ということになる。これを第一Foster展開すると $\begin{eqnarray}<br />Z(s)&=&\left(\frac{10000000}{9}\right)\frac{s\left(s^2+{\omega_3}^2\right)}{\left(s^2+{\omega_2}^2\right)\left(s^2+{\omega_4}^2\right)}\\<br />&=&\frac{H_1 s}{\left(s^2+{\omega_2}^2\right)}+\frac{H_2 s}{\left(s^2+{\omega_4}^2\right)}\\<br />&=&\frac{1}{C_1 s+\frac{1}{L_1 s}}+\frac{1}{C_2 s+\frac{1}{L_2 s}}\\<br />C_1&=&\frac{1}{H_1}=\frac{27}{12500000}=2.16\,[\mu F]\\<br />L_1&=&\frac{H_1}{{\omega_2}^2}=\frac{12500000}{27\cdot 2000^2}=115.7\,[mH]\\<br />C_2&=&\frac{1}{H_2}=\frac{27}{17500000}=1.543\,[\mu F]\\<br />L_2&=&\frac{H_2}{{\omega_4}^2}=\frac{17500000}{27\cdot 4000^2}=40.5\,[mH]\\<br />H_1&=&\lim_{s^2\to-{\omega_2}^2}\frac{\left(s^2+{\omega_2}^2\right)Z(s)}{s}\\<br />&=&\left.\left(\frac{10000000}{9}\right)\frac{\left(s^2+{\omega_3}^2\right)}{\left(s^2+{\omega_4}^2\right)}\right\|_{s^2=-{\omega_2}^2}\\<br />&=&\left(\frac{10000000}{9}\right)\frac{\left(-{\omega_2}^2+{\omega_3}^2\right)}{\left(-{\omega_2}^2+{\omega_4}^2\right)}\\<br />&=&\left(\frac{10000000}{9}\right)\frac{\left(-2000^2+3000^2\right)}{\left(-2000^2+4000^2\right)}\\<br />&=&\frac{12500000}{27}\\<br />H_2&=&\lim_{s^2\to-{\omega_4}^2}\frac{\left(s^2+{\omega_4}^2\right)Z(s)}{s}\\<br />&=&\left.\left(\frac{10000000}{9}\right)\frac{\left(s^2+{\omega_3}^2\right)}{\left(s^2+{\omega_2}^2\right)}\right\|_{s^2=-{\omega_4}^2}\\<br />&=&\left(\frac{10000000}{9}\right)\frac{\left(-{\omega_4}^2+{\omega_3}^2\right)}{\left(-{\omega_4}^2+{\omega_2}^2\right)}\\<br />&=&\left(\frac{10000000}{9}\right)\frac{\left(-4000^2+3000^2\right)}{\left(-4000^2+2000^2\right)}\\<br />&=&\frac{17500000}{27}\\<br />\end{eqnarray}$ ということになる。回路図に描くとということになる。

webadm	投稿日時: 2010-4-20 9:55
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【19】またまた：リアクタンス回路これでリアクタンス回路の問題は最後。以下の回路図で示されているリアクタンス回路と等価な回路をそれぞれ３つずつ示せというもの。与えられているのは第一Foster展開形のリアクタンス回路。したがって第二Foster展開形と第一と第二のCauer展開形の３つに展開し直せば良いことになる。回路から関数式を起こして展開し直してもよいが、回路素子の定数は問われていないのでその必要はない。第一Foster展開形と第二Foster展開形は互いに双対回路なので、並列と直列、インダクタンスとキャパシタンスが一対一で対応するのでそれでもよい。また第一Foster展開形と第二Foster我々は既に理論でFoster展開に関してω=0,∞が零点か極かの組み合わせによって回路の形が決まることを学んでいる。引用：これらのことから、Foster第一形式は以下の４ケースに分類される。 $\begin{array}<br />Case & \omega=0 & \omega=\infty & C_0 & L_\infty\\<br /> 1 & pole & pole & present & present\\<br /> 2 & zero & zero & short-circuited & short-circuited\\<br /> 3 & pole & zero & preset & short-circuited\\<br /> 4 & zero & pole & short-circuited & presetnt<br />\end{array}$ 同様のことがFoster第二形式についてもあてはまる。 $\begin{array}<br />Case & \omega=0 & \omega=\infty & L_0 & C_\infty\\<br /> 1 & pole & pole & present & present\\<br /> 2 & zero & zero & absent & absent\\<br /> 3 & pole & zero & preset & absent\\<br /> 4 & zero & pole & absent & presetnt<br />\end{array}$ また、Foster第一形式と第二形式は互いに逆の関係にあるので、同じ等価回路で一方が極をとるときその逆数は零点となり、その逆も真なりで、以下の対応関係が存在する。 $\begin{array}<br />first Foster form & second Foster form\\ 1 & 2\\ 2 & 1\\ 3 & 4\\ 4 & 3\end{array}$ 問題の回路はω=0に零点、ω=∞に極を持つので、第一Foster形のcase 4に該当する。第二Foster形では零点と極が逆になるcase 3が等価対応する形となる。従って回路図に描くとということになる。一方Cauer展開に関しても同様に以下のことを既に知っている。引用：第一Cauer形の場合 $\begin{array}<br />Case & \omega=0 & \omega=\infty & First element & Last element\\ 1 & pole & pole & L & C\\<br /> 2 & zero & zero & C & L\\<br /> 3 & pole & zero & C & C\\<br /> 4 & zero & pole & L & L<br />\end{array}$ 第二Cauer形の場合 $\begin{array}<br />Case & \omega=0 & \omega=\infty & First element & Last element\\<br /> 1 & pole & pole & L & C\\<br /> 2 & zero & zero & C & L\\<br /> 3 & pole & zero & C & C\\<br /> 4 & zero & pole & L & L<br />\end{array}$ ということになる。従って与えられた回路からω=0が零点、ω=∞が極である等価な第一Cauer展開形はLが直列、Cが並列接続され最初の素子と最後の素子が共にLとなりということになる。同様に第二Cauer展開形はLが並列、Cが直列で最初の素子と最後の素子が共にLとなりということになる。次ぎの回路は少々ひねってある。一見すると第二Cauer形に見えるが最後の素子が２つのCの直列になっている。これはブービートラップみたいなひっかけで、教科書暗記式で問題に臨もうとするやからを排除するための問題である。賢明な読者ならもうお分かりの通り、最後のC4とC5はキャパシタンスを直列に接続した合成キャパシタンスとして一個の等価Cと見なすことができる。従って第一素子がLで最終素子がCなので、第二Cauer形のcase 2に該当する。ω=0,∞が共に零点であることからもそれとわかる。従って第一Cauer形ではLが直列接続、Cが並列接続となり第一素子がCで最終素子がLなのでということになる。同様に第一Foster展開でω=0,∞が共に零点であるcaseではC0,L∞が存在しないのでLC並列回路の直列接続のみとなりということになる。第二Foster展開ではω=0,∞あ共に極となるcaseが対応するのでL0,C∞が共に存在しということになる。ちょっと気になるのが、第一Foster形ではLC並列回路が２つあったのに、第二Foster形ではLC直列回路がひとつしか現れない点である。疑問に思われるのは当然であるので、確かめてみよう。第一Foster形の回路からリアクタンス関数の式を起こすと $\begin{array}<br />Z(s)&=&\frac{1}{\frac{1}{s\,L_2}+s\,C_2}+\frac{1}{\frac{1}{s\,L_1}+s\,C_1}\\<br />&=&\left(\frac{C_1+C_2}{C_1 C_2}\right)\frac{s\,\left( {s}^{2}+\frac{L_1+L_2}{\left(C_1+C_2\right)L_1 L_2}\right) }{\left(s^2+\frac{1}{C_1 L_1}\right)\left(s^2+\frac{1}{C_2 L_2}\right)}<br />\end{eqnarray}$ これを第二Foster形に展開するためにアドミッタンスの総和に部分分数展開すると $\begin{array}<br />Y(s)&=&\frac{1}{Z(s)}\\<br />&=&\left(\frac{C_1 C_2}{C_1+C_2}\right)\frac{\left(s^2+\frac{1}{C_1 L_1}\right)\left(s^2+\frac{1}{C_2 L_2}\right)}{s\,\left( {s}^{2}+\frac{L_1+L_2}{\left(C_1+C_2\right)L_1 L_2}\right) }\\<br />&=&\left(\frac{C_1 C_2}{C_1+C_2}\right)\left(s+\frac{C_1+C_2}{s\,C_1 C_2\left( L1+L2\right)\left(\right)}+\frac{s\,\left( {C2}\,{L2}-{C1}^\,{L1}\right)^2 }{C_1 C_2 L_1 L_2\left( L_1+L_2\right)\left(C_1+C_2\right)\,\left( {s}^{2}+\frac{L_1+L_2}{L_1 L_2\left(C_1+C_2\right)}\right) }\right)\\<br />&=&L_0 s+\frac{1}{C_\infty s}+\frac{1}{C_1 s+\frac{1}{L_1 s}}<br />\end{eqnarray}$ ということで間違いではない。良く考えれば当然だが、第三項は誘導性か容量性かどちらかのアドミッタンス値（正か負のいずれか）をとる。一方L0とC∞のアドミッタンスの総和も誘導性か容量性のいずれかのアドミッタンス値をとり、全部を足すとゼロになる条件が第三項が誘導性か容量性かによって2ケース存在することになる。これが第一Foster形が持つ２つの極の双対となる零点となるのだった。

« 1 (2) 3 4 »

スレッド表示 | 新しいものから

前のトピック | 次のトピック | トップ

投稿するにはまず登録を