Gan's blog - フォーラム

« 1 2 (3) 4 »

投稿者	スレッド
webadm	投稿日時: 2010-4-21 23:11
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【20】インピーダンス関数終わったと思っていた正実関数の問題が再び出てきた。以下の関数が正実関数となる正の実数なる係数、a,b,cの間の関係条件を示せというもの。加えてRL回路またはRC回路のインピーダンス関数として実現されるにはa,b,cにどのような条件が必要が示せというもの。 $Z(s)=\frac{s+c}{\left(s+a\right)\left(s+b\right)}$ s=jωと置くとインピーダンス関数の実数部は $\begin{eqnarray}<br />Re\left(Z(j\omega)\right)&=&\frac{j\omega+c}{\left(j\omega+a\right)\left(j\omega+b\right)}\\<br />&=&Re\left(\frac{j\omega+c}{ab-{\omega}^2+j\left(a+b\right)\omega}\right)\\<br />&=&Re\left(\frac{\left(j\omega+c\right)\left(\left(ab-{\omega}^2\right)-j\left(a+b\right)\omega\right)}{\left(\left(ab-{\omega}^2\right)^2+\left(a+b\right)^2\omega^2\right)}\right)\\<br />&=&\frac{\left(a+b\right)\omega^2+c\left(ab-{\omega}^2\right)}{{\omega}^4-\cancel{2ab{\omega}^2}+a^2b^2+\left(a^2+\cancel{2ab}+b^2\right)\omega^2}\\<br />&=&\frac{\left(a+b-c\right)\omega^2+abc}{\left(s^2+a^2\right)\left(s^2+b^2\right)}\ge 0\,\forall\omega<br />\end{eqnarray}$ ということになる。すなわち正実関数であるための必要十分条件は $\begin{eqnarray}<br />a+b-c\ge0\\<br />a+b\ge c<br />\end{eqnarray}$ ということになる。 RL回路、RC回路はLC回路と同様に零点と極が交互に現れる必要から問題の関数では実軸上に-a,-bの２つの極と-cに零点を持つことから a＜c＜b もしくは b＜c＜a ということになる。著者の解答ではa≦c≦bもしくはb≦c≦aとあるが、a,b,cが互いに等しいものがあると零点と極が消滅してしまうので元のインピーダンス関数とは違ってしまう。

webadm	投稿日時: 2010-4-22 12:29
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【21】続：インピーダンス関数しばらくインピーダンス関数に関わる問題が続く。与えられた関数がインピーダンスとして実現できるか否かを判定し、実現できるものについては二種類の受動素子だけで実現できるかどうかを調べよというもの。 $\text{(1)}\,\frac{s\left(s^2+5\right)\left(s^2+6\right)}{\left(s^2+3\right)\left(s^2+4\right)}$ これは零点と極がいずれも一位で虚軸上に存在するため正実関数の必要条件を満たすものの、リアクタンス関数の必要条件である零点と極が交互に並ぶ条件を満たしていない。実際に部分分数展開してみるとはっきりする。 $\begin{eqnarray}<br />Z(s)&=&\frac{s\left(s^2+5\right)\left(s^2+6\right)}{\left(s^2+3\right)\left(s^2+4\right)}\\<br />&=&-\frac{2\,s}{{s}^{2}+4}+\frac{6\,s}{{s}^{2}+3}+s<br />\end{eqnarray}$ 負の留数を持つので正実関数の必要条件を満たしておらず２種類の受動素子では実現できない。 $\text{(2)}\,\frac{\left(s+5\right)}{\left(s+3\right)\left(s+4\right)}$ これは零点と極がいずれも実軸上で左半面にあり正実関数の必要条件を満たしているが、零点と極が交互に並んでないため十分ではない。これも部分分数に展開してみると $\begin{eqnarray}<br />Z(s)&=&\frac{\left(s+5\right)}{\left(s+3\right)\left(s+4\right)}\\<br />&=&\frac{2}{s+3}-\frac{1}{s+4}<br />\end{eqnarray}$ 負の留数を伴うため二種類の受動素子だけでは実現できない。 $\text{(3)}\,\frac{\left(s+1\right)\left(s+3\right)}{\left(s+2\right)}$ これは零点と極が実軸上にあり、交互に現れることからよさそうである。部分分数展開してみると $\begin{eqnarray}<br />Z(s)&=&\frac{\left(s+1\right)\left(s+3\right)}{\left(s+2\right)}\\<br />&=&\frac{1}{\frac{\left(s+2\right)}{\left(s+1\right)\left(s+3\right)}}\\<br />&=&\frac{1}{\frac{1}{2\,\left( s+3\right) }+\frac{1}{2\,\left( s+1\right) }}\\<br />&=&\frac{1}{\frac{1}{L_1 s+R_1}+\frac{1}{L_2 s+R_2}}\\<br />L_1&=&2\,[H]\\<br />R_1&=&6\,[\Omega]\\<br />L_2&=&2\,[H]\\<br />R_2&=&2\,[\Omega]<br />\end{eqnarray}$ 従って２つのLR直列回路が並列に接続された回路で実現できることになる。 $\text{(4)}\,\frac{s^3+6s}{\left(s^2+5\right)\left(s^2+7\right)}$ 分子の多項式が因数分解されていないが、零点と極がいずれも一位で虚軸上にのみ現れるので正実関数かつリアクタンス関数である。部分分数展開すると $\begin{eqnarray}<br />Z(s)&=&\frac{s^3+6s}{\left(s^2+5\right)\left(s^2+7\right)}\\<br />&=&\frac{s\left(s^2+6\right)}{\left(s^2+5\right)\left(s^2+7\right)}\\<br />&=&\frac{s}{2\,\left( {s}^{2}+7\right) }+\frac{s}{2\,\left( {s}^{2}+5\right) }\\<br />&=&\frac{1}{C_1 s+\frac{1}{L_1 s}}+\frac{1}{C_2 s+\frac{1}{L_2 s}}\\<br />C_1&=&2\,[F]\\<br />L_1&=&\frac{1}{14}\,[H]\\<br />C_2&=&2\,[F]\\<br />L_2&=&\frac{1}{10}\,[H]<br />\end{eqnarray}$ 従って２つのLC並列回路の直列接続で実現できる。ここだけの話だが分子の式を最初書き写し間違えてs^3がs^2になっていて次数が一つ足らず零点が実軸上に現れてしまう変な式になってしまって焦ったのは内緒だ。 $\text{(5)}\,\frac{s^2+2}{\left(s+2\right)\left(s+3\right)}$ これは零点が虚軸上に極が実軸上にあるので正実関数のように見えるがs=jωとして正実関数であるためには $\begin{eqnarray}<br />Re\left(Z(j\omega)\right)&=&Re\left(\frac{-{\omega}^2+2}{\left(j\omega+2\right)\left(j\omega+3\right)}\right)\\<br />&=&Re\left(\frac{2-{\omega}^2}{6-{\omega}^2+j5\omega}\right)\\<br />&=&Re\left(\frac{\left(2-{\omega}^2\right)\left(6-{\omega}^2-j5\omega\right)}{\left(6-{\omega}^2\right)^2+\left(5\omega\right)^2}\right)\\<br />&=&\frac{\left(2-{\omega}^2\right)\left(6-{\omega}^2\right)}{\left(6-{\omega}^2\right)^2+\left(5\omega\right)^2}\ge0\,\forall\omega<br />\end{eqnarray}$ を満足しなければならないが、 2＜ω^2＜6 の範囲では条件を満たさないので正実関数ではないということになる。 $\text{(6)}\,\frac{\left(s+4\right)\left(s+7\right)}{\left(s+3\right)\left(s+6\right)}$ これは零点と極が一位で実軸上かつ左半面にのみ存在し、零点と極が交互に位置しているのでよさそうである。s=jωと置いて実数部を確かめてみると $\begin{eqnarray}<br />Re\left(Z(j\omega)\right)&=&Re\left(\frac{\left(j\omega+4\right)\left(j\omega+7\right)}{\left(j\omega+3\right)\left(j\omega+6\right)}\right)\\<br />&=&Re\left(\frac{28-{\omega}^2+j11\omega}{18-{\omega}^2+j9\omega}\right)\\<br />&=&Re\left(\left(\frac{28-{\omega}^2+j11\omega\right)\left(18-{\omega}^2-j9\omega\right)}{\left(18-{\omega}^2\right)^2+\left(9\omega\right)^2}\right)\\<br />&=&\frac{\left(28-{\omega}^2\right)\left(18-{\omega}^2\right)+99\omega^2}{\left(18-{\omega}^2\right)^2+\left(9\omega\right)^2}\\<br />&=&\frac{{\omega}^4+53\omega^2+504}{\left(18-{\omega}^2\right)^2+\left(9\omega\right)^2}\ge0\,\forall\omega<br />\end{eqnarray}$ が成り立つので正実関数である。部分分数に展開すると $\begin{eqnarray}<br />Z(s)&=&\frac{\left(s+4\right)\left(s+7\right)}{\left(s+3\right)\left(s+6\right)}\\<br />&=&\frac{H_1}{s+3}+\frac{H_2}{s+6}+H_\infty\\<br />&=&\frac{1}{C_1 s+G_1}+\frac{1}{C_2 s+G_2}+R_\infty\\<br />C_1&=&\frac{1}{H_1}=\frac{3}{4}\,[F]\\<br />G_1&=&\frac{3}{H_1}=\frac{9}{4}\,[S]\\<br />C_2&=&\frac{1}{H_2}=\frac{3}{2}\,[F]\\<br />G_2&=&\frac{6}{H_2}=\frac{18}{2}\,[S]\\<br />R_\infty&=&H_\infty=1\,[\Omega]\\<br />H_1&=&\lim_{s\to-3}\left(s+3\right)Z(s)\\<br />&=&\left.\frac{\left(s+4\right)\left(s+7\right)}{\left(s+6\right)}\right\|_{s=-3}\\<br />&=&\frac{\left(-3+4\right)\left(-3+7\right)}{\left(-3+6\right)}\\<br />&=&\frac{4}{3}\\<br />H_2&=&\lim_{s\to-6}\left(s+6\right)Z(s)\\<br />&=&\left.\frac{\left(s+4\right)\left(s+7\right)}{\left(s+3\right))}\right\|_{s=-6}\\<br />&=&\frac{\left(-6+4\right)\left(-6+7\right)}{\left(-6+3\right))}\\<br />&=&\frac{2}{3}\\<br />H_\infty&=&\lim_{s\to\infty}Z(s)\\<br />&=&\left.\frac{\left(s+4\right)\left(s+7\right)}{\left(s+3\right)\left(s+6\right)}\right\|_{s=\infty}\\<br />&=&\left.\frac{\left(1+\frac{4}{s}\right)\left(1+\frac{7}{s}\right)}{\left(1+\frac{3}{s}\right)\left(1+\frac{6}{s}\right)}\right\|_{s=\infty}\\<br />&=&1<br />\end{eqnarray}$ ということで２つのRC並列回路とひとつの抵抗の直列接続で実現できる。 $\text{(7)}\,\frac{2}{s+3}+2-\frac{2}{s+4}$ これは一見すると有理関数の形をしていないのと分子の係数に負の値があるので正実関数でないように見えるが、s=jωとして実数部を調べてみると $\begin{eqnarray}<br />Re\left(Z(j\omega)\right)&=&Re\left(\frac{2}{j\omega+3}+2-\frac{2}{j\omega+4}\right)\\<br />&=&Re\left(\frac{2\left(j\omega+4\right)+2\left(j\omega+3\right)\left(j\omega+4\right)-2\left(j\omega+3\right)}{\left(j\omega+3\right)\left(j\omega+4\right)}\right)\\<br />&=&Re\left(\frac{\cancel{j2\omega}+8+2\left(12-{\omega}^2+j7\omega\right)-\cancel{j2\omega}-6}{12-{\omega}^2+j7\omega}\right)\\<br />&=&Re\left(\frac{\left(26-2{\omega}^2+j14\omega\right)\left(12-{\omega}^2-j7\omega\right)}{\left(12-{\omega}^2\right)^2+\left(7\omega\right)^2}\right)\\<br />&=&\frac{\left(26-2{\omega}^2\right)\left(12-{\omega}^2\right)+98\omega^2}{\left(12-{\omega}^2\right)^2+\left(7\omega\right)^2}\\<br />&=&\frac{2{\omega}^4+48\omega^2+312}{\left(12-{\omega}^2\right)^2+\left(7\omega\right)^2}\ge0\,\forall\omega<br />\end{eqnarray}$ が成立するので正実関数である。部分分数展開すると $\begin{eqnarray}<br />Z(s)&=&\frac{2}{s+3}+2-\frac{2}{s+4}\\<br />&=&\frac{2}{s+3}+\frac{2s+6}{s+4}\\<br />&=&\frac{2}{s+3}+\frac{2s}{s+4}+\frac{6}{s+4}\\<br />&=&\frac{1}{C_1 s+G_1}+\frac{1}{G_2+\frac{1}{L_2 s}}+\frac{1}{C_3 s+G_3}\\<br />C_1&=&\frac{1}{2}\,[F]\\<br />G_1&=&\frac{3}{2}\,[S]\\<br />G_2&=&\frac{1}{2}\,[S]\\<br />L_2&=&\frac{1}{2}\,[H]\\<br />C_3&=&\frac{1}{6}\,[F]\\<br />G_3&=&\frac{2}{3}\,[S]<br />\end{eqnarray}$ ということで２つのRC並列回路とひとつのRL並列回路の直列接続が必要となり、２種類の素子だけでは実現できないということになる。 $\text{(8)}\,\frac{s^3+9s^2+23s+15}{s^2+6s+8}$ これはなんだか判らないけど、s=jωとして実数部を調べてみると $\begin{eqnarray}<br />Re\left(Z(j\omega)\right)&=&Re\left(\frac{-j{\omega}^3-9{\omega}^2+j23\omega+15}{-{\omega}^2+j6\omega+8}\right)\\<br />&=&Re\left(\frac{\left(15-9{\omega}^2+j\omega\left(23-{\omega}^2\right)\right)\left(8-{\omega}^2-j6\omega\right)}{\left(8-{\omega}^2\right)^2+\left(6\omega\right)^2}\right)\\<br />&=&\frac{\left(15-9{\omega}^2\right)\left(8-{\omega}^2\right)+6{\omega}^2\left(23-{\omega}^2\right)}{\left(8-{\omega}^2\right)^2+\left(6\omega\right)^2}\\<br />&=&\frac{9{\omega}^4-87{\omega}^2+120+138{\omega}^2-6{\omega}^4}{\left(8-{\omega}^2\right)^2+\left(6\omega\right)^2}\\<br />&=&\frac{3{\omega}^4+51{\omega}^2+120}{\left(8-{\omega}^2\right)^2+\left(6\omega\right)^2}\ge0\,\forall\omega<br />\end{eqnarray}$ が成り立つので正実関数である。部分分数展開してみると $\begin{eqnarray}<br />Z(s)&=&\frac{s^3+9s^2+23s+15}{s^2+6s+8}\\<br />&=&\frac{\left(s+1\right)\left(s+3\right)\left(s+5\right)}{\left(s+2\right)\left(s+4\right)}\\<br />&=&\frac{1}{\frac{\left(s+2\right)\left(s+4\right)}{\left(s+1\right)\left(s+3\right)\left(s+5\right)}}\\<br />&=&\frac{1}{\frac{H_1}{s+1}+\frac{H_2}{s+3}+\frac{H_3}{s+5}}\\<br />&=&\frac{1}{\frac{1}{L_1 s+R_1}+\frac{1}{L_2 s+R_2}+\frac{1}{L_3 s+R_3}}\\<br />L_1&=&\frac{1}{H_1}=\frac{8}{3}\,[H]\\<br />R_1&=&\frac{1}{H_1}=\frac{3}{8}\,[\Omega]\\<br />L_2&=&\frac{1}{H_2}=4\,[H]\\<br />R_2&=&\frac{3}{H_2}=12\,[\Omega]\\<br />L_3&=&\frac{1}{H_3}=\frac{8}{3}\,[H]\\<br />R_3&=&\frac{5}{H_3}=\frac{40}{3}\,[\Omega]\\<br />H_1&=&\lim_{s\to-1}\left(s+1\right)Y(s)\\<br />&=&\left.\frac{\left(s+2\right)\left(s+4\right)}{\left(s+3\right)\left(s+5\right)}\right\|_{s=-1}\\<br />&=&\frac{\left(-1+2\right)\left(-1+4\right)}{\left(-1+3\right)\left(-1+5\right)}\\<br />&=&\frac{3}{8}\\<br />H_2&=&\lim_{s\to-3}\left(s+3\right)Y(s)\\<br />&=&\left.\frac{\left(s+2\right)\left(s+4\right)}{\left(s+1\right)\left(s+5\right)}\right\|_{s=-3}\\<br />&=&\frac{\left(-3+2\right)\left(-3+4\right)}{\left(-3+1\right)\left(-3+5\right)}\\<br />&=&\frac{1}{4}\\<br />H_3&=&\lim_{s\to-5}\left(s+5\right)Y(s)\\<br />&=&\left.\frac{\left(s+2\right)\left(s+4\right)}{\left(s+1\right)\left(s+3\right)}\right\|_{s=-5}\\<br />&=&\frac{\left(-5+2\right)\left(-5+4\right)}{\left(-5+1\right)\left(-5+3\right)}\\<br />&=&\frac{3}{8}<br />\end{eqnarray}$ ということで３つのRL直列回路の並列接続で実現できるため２種類の素子で実現可能。 $\text{(9)}\,\frac{s^2+10}{\left(s+5\right)\left(s+2\right)}$ 最後のは零点が複素共役対で極が実軸上でそれぞれ左半面にあるがどうだろう。s=jωとして実数部を調べてみると $\begin{eqnarray}<br />Re\left(Z(j\omega)\right)&=&Re\left(\frac{-{\omega}^2+10}{\left(j\omega+5\right)\left(j\omega+2\right)}\right)\\<br />&=&Re\left(\frac{10-{\omega}^2}{10-{\omega}^2+j7\omega}\right)\\<br />&=&Re\left(\frac{\left(10-{\omega}^2\right)\left(10-{\omega}^2-j7\omega\right)}{\left(10-{\omega}^2\right)^2+\left(7\omega\right)^2}\right)\\<br />&=&\frac{\left(10-{\omega}^2\right)^2}{\left(10-{\omega}^2\right)^2+\left(7\omega\right)^2}\ge0\,\forall\omega<br />\end{eqnarray}$ が成り立つので正実関数ではあるが、零点と極が交互に現れないので受動素子だけでは実現できない。部分分数展開してみても $\begin{eqnarray}<br />Z(s)&=&\frac{s^2+10}{\left(s+5\right)\left(s+2\right)}\\<br />&=&\frac{H_1}{s+5}+\frac{H_2}{s+2}+H_\infty\\<br />H_1&=&\lim_{s\to-5}\left(s+5\right)Z(s)\\<br />&=&\left.\frac{s^2+10}{\left(s+2\right)}\right\|_{s=-5}<br />&=&\frac{5^+10}{\left(-5+2\right)}\\<br />&=&-\frac{35}{3}\\<br />H_2&=&\lim_{s\to-2}\left(s+2\right)Z(s)\\<br />&=&\left.\frac{s^2+10}{\left(s+5\right)}\right\|_{s=-2}<br />&=&\frac{2^2+10}{\left(-2+5\right)}\\<br />&=&-\frac{14}{3}\\<br />H_\infty&=&\lim_{s\to\infty}Z(s)\\<br />&=&\left.\frac{s^2+10}{\left(s+5\right)\left(s+2\right)}\right\|_{s=\infty}\\<br />&=&\left.\frac{1+\frac{10}{s^2}}{\left(1+\frac{5}{s}\right)\left(1+\frac{2}{s}\right)}\right\|_{s=\infty}\\<br />&=&1<br />\end{eqnarray}$ という具合に負の留数を持つため受動素子だけでは実現できないことになる。こうしてみると複素共役対の特異点を持つ関数も正実関数であるものの、負の留数を持つため受動素子だけでは実現できないが、負のインダクタンスやキャパシタンス、負の抵抗は真空管やトランジスタのような能動素子を使用すれば実現できる。特に複素平面上の楕円曲線上に複素共役対として複数の特異点を持つ楕円有理関数はフィルターとして良好な周波数特性を備える。後々これら楕円関数フィルターに関して学ぶにも基礎となる二端子回路の理論を知っておく必要がある。

webadm	投稿日時: 2010-4-24 4:03
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【22】続々：インピーダンス関数次ぎもインピーダンス関数の問題で、以下に示された関数をCauer展開し二種類の受動素子だけで実現できるか確かめ、実現できるものについては回路を示せというもの。 $\text{(1)}\,Z_a(s)=\frac{15s^4+166s^2+144}{10s^3+84s}$ 分子の次数が分母よりも大きいので次数の大きな項から切り出していくことにする。 $\begin{eqnarray}<br />Z_a(s)&=&\frac{15s^4+166s^2+144}{10s^3+84s}\\<br />&=&\frac{15}{10}s+\frac{\left(166-\frac{15\cdot 84}{10}\right)s^2+144}{10s^3+84s}\\<br />&=&\frac{3}{2}s+\frac{1}{\Large\frac{10s^3+84s}{40s^2+144}}\\<br />&=&\frac{3}{2}s+\frac{1}{\Large\frac{10}{40}s+\frac{\left(84-\frac{10\cdot 144}{40}\right)s}{40s^2+144}}\\<br />&=&\frac{3}{2}s+\frac{1}{\Large\frac{1}{4}s+\frac{48s}{40s^2+144}}\\<br />&=&\frac{3}{2}s+\frac{1}{\Large\frac{1}{4}s+\frac{1}{\frac{5}{6}s+\frac{144}{48s}}}\\<br />&=&\frac{3}{2}s+\frac{1}{\Large\frac{1}{4}s+\frac{1}{\frac{5}{6}s+\frac{3}{s}}}\\<br />&=&L_1 s+\frac{1}{\Large C_2 s+\frac{1}{L_3 s+\frac{1}{C_4 s}}}\\<br />L_1&=&\frac{3}{2}\,[H]\\<br />C_2&=&\frac{1}{4}\,[F]\\<br />L_3&=&\frac{5}{6}\,[H]\\<br />C_4&=&\frac{1}{3}\,[F]<br />\end{eqnarray}$ 従ってLとCの二種類の受動素子のラダー回路で実現できる。回路図を描くとということになる。 $\text{(2)}\,Z_b(s)=\frac{18s^3+6s^2+6s+1}{6s^2+2s+1}$ 次ぎも同様に次数の大きな項から切り出していくと $\begin{eqnarray}<br />Z_b(s)&=&\frac{18s^3+6s^2+6s+1}{6s^2+2s+1}\\<br />&=&\frac{18}{6}s+\frac{\left(6-\frac{18\cdot 2}{6}\right)s^2+\left(6-\frac{18}{6}\right)s+1}{6s^2+2s+1}\\<br />&=&3s+\frac{3s+1}{6s^2+2s+1}\\<br />&=&3s+\frac{1}{\Large\frac{6s^2+2s+1}{3s+1}}\\<br />&=&3s+\frac{1}{\Large 2s+\frac{1}{3s+1}}\\<br />&=&L_1 s+\frac{1}{\Large C_2 s+\frac{1}{L_3 s+R_4}}\\<br />L_1&=&3\,[H]\\<br />C_2&=&2\,[F]\\<br />L_3&=&3\,[H]\\<br />R_4&=&1\,[\Omega]<br />\end{eqnarray}$ 従ってLCRラダー回路となるため二種類の素子だけでは実現できない。 $\text{(3)}\,Z_c(s)=\frac{36s^4+4s^2-1}{18s^3-s}$ これはリアクタンス関数ぽいが負の定数項がある時点でアウトだろうと思う。一応次数の高い項から切り出すと $\begin{eqnarray}<br />Z_c(s)&=&\frac{36s^4+4s^2-1}{18s^3-s}\\<br />&=&\frac{36}{18}s+\frac{\left(4+\frac{36}{18}\right)s^2-1}{18s^3-s}\\<br />&=&2s+\frac{1}{\Large\frac{18}{6}s+\frac{\left(\frac{18}{6}-1\right)s}{6s^2-1}}\\<br />&=&2s+\frac{1}{\Large\frac{18}{6}s+\frac{2s}{6s^2-1}}\\<br />&=&2s+\frac{1}{\Large 3s+\frac{1}{3s-\frac{1}{2s}}}\\<br />&=&L_1 s+\frac{1}{\Large C_2 s+\frac{1}{L_3 s+\frac{1}{C_4 s}}}\\<br />L_1&=&2\,[H]\\<br />C_2&=&3\,[F]\\<br />L_3&=&3\,[H]\\<br />C_4&=&-2\,[F]<br />\end{eqnarray}$ 最後の素子が負のキャパシタンスを持つことから２種類の受動素子では実現できない。 $\text{(4)}\,Z_d(s)=\frac{576s^3+388s^2+55s+1}{288s^2+122s+9}$ 最後のはまともそうだ。次数の高い項から切り出すと $\begin{eqnarray}<br />Z_d(s)&=&\frac{576s^3+388s^2+55s+1}{288s^2+122s+9}\\<br />&=&\frac{576}{288}s+\frac{\left(388-\frac{576\cdot 122}{288}\right)s^2+\left(55-\frac{576\cdot 9}{288}\right)s+1}{288s^2+122s+9}\\<br />&=&2s+\frac{\144s^2+37s+1}{288s^2+122s+9}\\<br />&=&2s+\frac{1}{\Large 2+\frac{\left(122-2\cdot 37\right)s+\left(9-2\right)}{\144s^2+37s+1}}\\<br />&=&2s+\frac{1}{\Large 2+\frac{1}{\frac{\144s^2+37s+1}{48s+7}}}\\<br />&=&2s+\frac{1}{\Large 2+\frac{1}{\frac{144}{48}s+\frac{\left(37-\frac{144\cdot 7}{48}\right)s+1}{48s+7}}}\\<br />&=&2s+\frac{1}{\Large 2+\frac{1}{3s+\frac{1}{\frac{48s+7}{16s+1}}}}\\<br />&=&2s+\frac{1}{\Large 2+\frac{1}{3s+\frac{1}{3+\frac{4}{16s+1}}}}\\<br />&=&L_1 s+\frac{1}{\Large G_2+\frac{1}{L_3 s+\frac{1}{G_4+\frac{4}{L_5 s+R_6}}}}\\<br />L_1&=&2\,[H]\\<br />G_2&=&2\,[S]\\<br />L_3&=&3\,[H]\\<br />G_4&=&3\,[S]\\<br />L_5&=&2\,[H]\\<br />R_6&=&\frac{1}{4}\,[\Omega]<br />\end{eqnarray}$ 従ってRLラダー回路で構成できる。回路図で表すとということになる。

webadm	投稿日時: 2010-4-24 11:55
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【23】またまた：インピーダンス関数前問はインピーダンス関数をCauer展開だったが、今度はインピーダンス関数のFoster展開問題。以下の関数から２種類のFoster形回路を合成せよというもの。 $\text{(1)}\,Z_1(s)=\frac{\left(s+3\right)\left(s+5\right)}{\left(s+2\right)\left(s+4\right)}$ 第一Foster形だとインピーダンスの総和に展開されるので $\begin{eqnarray}<br />Z_1(s)&=&\frac{\left(s+3\right)\left(s+5\right)}{\left(s+2\right)\left(s+4\right)}\\<br />&=&\frac{H_1}{s+2}+\frac{H_2}{s+4}+H_\infty\\<br />&=&\frac{1}{C_1 s+G_1}+\frac{1}{C_2 s+G_2}+R_\infty\\<br />C_1&=&\frac{1}{H_1}=\frac{2}{3}\,[F]\\<br />G_1&=&\frac{2}{H_1}=\frac{4}{3}\,[S]\\<br />C_2&=&\frac{1}{H_2}=2\,[F]\\<br />G_2&=&\frac{4}{H_2}=8\,[S]\\<br />R_\infty&=&H_\infty=1\,[\Omega]\\<br />H_1&=&\lim_{s\to-2}\left(s+2\right)Z_1(s)\\<br />&=&\left.\frac{\left(s+3\right)\left(s+5\right)}{\left(s+4\right)}\right\|_{s=-2}\\<br />&=&\frac{\left(-2+3\right)\left(-2+5\right)}{\left(-2+4\right)}\\<br />&=&\frac{3}{2}\\<br />H_2&=&\lim_{s\to-4}\left(s+4\right)Z_1(s)\\<br />&=&\left.\frac{\left(s+3\right)\left(s+5\right)}{\left(s+2\right)}\right\|_{s=-4}\\<br />&=&\frac{\left(-4+3\right)\left(-4+5\right)}{\left(-4+2\right)}\\<br />&=&\frac{1}{2}\\<br />H_\infty&=&\lim_{s\to\infty}Z_1(s)\\<br />&=&\left.\frac{\left(s+3\right)\left(s+5\right)}{\left(s+2\right)\left(s+4\right)}\right\|_{s=\infty}\\<br />&=&\left.\frac{\left(1+\frac{3}{s}\right)\left(1+\frac{5}{s}\right)}{\left(1+\frac{2}{s}\right)\left(1+\frac{4}{s}\right)}\right\|_{s=\infty}\\<br />&=&1<br />\end{eqnarra}$ これは２つのRC並列回路と抵抗の直列接続となる。回路図に表すとということになる。もうひとつ第二Foster形は単純にアドミッタンスの総和へ部分分数展開すると負の留数が出てしまうのでちょっと操作する必要がある $\begin{eqnarray}<br />Y_1(s)&=&\frac{1}{Z_1(s)}\\<br />&=&\frac{\left(s+2\right)\left(s+4\right)}{\left(s+3\right)\left(s+5\right)}\\<br />&=&s\left(\frac{\left(s+2\right)\left(s+4\right)}{s\left(s+3\right)\left(s+5\right)}\right)\\<br />&=&s\left(\frac{H_0}{s}+\frac{H_1}{s+3}+\frac{H_2}{s+5}\right)\\<br />&=&H_0+\frac{H_1 s}{s+3}+\frac{H_2 s}{s+5}\\<br />&=&G_0+\frac{1}{R_1+\frac{1}{C_1 s}}+\frac{1}{R_2+\frac{1}{C_2 s}}\\<br />G_0&=&H_0=\frac{8}{15}\,[S]\\<br />R_1&=&\frac{1}{H_1}=6\,[\Omega]\\<br />C_1&=&\frac{H_1}{3}=\frac{1}{18}\,[F]\\<br />R_2&=&\frac{1}{H_2}=\frac{10}{3}\,[\Omega]\\<br />C_2&=&\frac{H_2}{5}=\frac{3}{50}\,[F]\\<br />H_0&=&\lim_{s\to0}Y_1(s)\\<br />&=&\left.\frac{\left(s+2\right)\left(s+4\right)}{\left(s+3\right)\left(s+5\right)}\right\|_{s=0}\\<br />&=&\frac{\left(0+2\right)\left(0+4\right)}{\left(0+3\right)\left(0+5\right)}\\<br />&=&\frac{8}{15}\\<br />H_1&=&\lim_{s\to-3}\frac{\left(s+3\right)Y_1(s)}{s}\\<br />&=&\left.\frac{\left(s+2\right)\left(s+4\right)}{s\left(s+5\right)}\right\|_{s=-3}\\<br />&=&\frac{\left(-3+2\right)\left(-3+4\right)}{-3\left(-3+5\right)}\\<br />&=&\frac{1}{6}\\<br />H_2&=&\lim_{s\to-5}\frac{\left(s+5\right)Y_1(s)}{s}\\<br />&=&\left.\frac{\left(s+2\right)\left(s+4\right)}{s\left(s+3\right)}\right\|_{s=-4}\\<br />&=&\frac{\left(-5+2\right)\left(-5+4\right)}{-5\left(-5+3\right)}\\<br />&=&\frac{3}{10}<br />\end{eqnarra}$ 従って２つのRC直列回路と抵抗の並列接続で構成される。回路図に描くとということになる。 $\text{(2)}\,Z_2(s)=\frac{s\left(s+3\right)\left(s+5\right)}{\left(s+2\right)\left(s+4\right)}$ 前の設問の式の分子の次数がひとつ多くなっただけだが、単純に部分分数展開すると負の留数が出てしまうのでちょっとした数式操作が必要だ。 $\begin{eqnarray}<br />Z_2(s)&=&\frac{s\left(s+3\right)\left(s+5\right)}{\left(s+2\right)\left(s+4\right)}\\<br />&=&s\left(\frac{\left(s+3\right)\left(s+5\right)}{\left(s+2\right)\left(s+4\right)}\right)\\<br />&=&s\left(\frac{H_1}{s+2}+\frac{H_2}{s+4}+H_\infty\right)\\<br />&=&\frac{H_1 s}{s+2}+\frac{H_2 s}{s+4}+H_\infty s\\<br />&=&\frac{1}{G_1+\frac{1}{L_1 s}}+\frac{1}{G_2+\frac{1}{L_2 s}}+L_\infty s\\<br />G_1&=&\frac{1}{H_1}=\frac{2}{3}\,[S]\\<br />L_1&=&\frac{H_1}{2}=\frac{3}{4}\,[H]\\<br />G_2&=&\frac{1}{H_2}=2\,[S]\\<br />L_2&=&\frac{H_2}{4}=\frac{1}{8}\,[H]\\<br />L_\infty&=&H_\infty=1\,[H]\\<br />H_1&=&\lim_{s\to-2}\frac{\left(s+2\right)Z_2(s)}{s}\\<br />&=&\left.\frac{\left(s+3\right)\left(s+5\right)}{\left(s+4\right)}\right\|_{s=-2}\\<br />&=&\frac{\left(-2+3\right)\left(-2+5\right)}{\left(-2+4\right)}\\<br />&=&\frac{3}{2}\\<br />H_2&=&\lim_{s\to-4}\frac{\left(s+4\right)Z_2(s)}{s}\\<br />&=&\left.\frac{\left(s+3\right)\left(s+5\right)}{\left(s+2\right)}\right\|_{s=-4}\\<br />&=&\frac{\left(-4+3\right)\left(-4+5\right)}{\left(-4+2\right)}\\<br />&=&\frac{1}{2}\\<br />H_\infty&=&\lim_{s\to\infty}\frac{Z_2(s)}{s}\\<br />&=&\left.\frac{\left(s+3\right)\left(s+5\right)}{\left(s+2\right)\left(s+4\right)}\right\|_{s=\infty}\\<br />&=&\left.\frac{\left(1+\frac{3}{s}\right)\left(1+\frac{5}{s}\right)}{\left(1+\frac{2}{s}\right)\left(1+\frac{4}{s}\right)}\right\|_{s=\infty}\\<br />&=&1<br />\end{eqnarray}$ 従って２つのRL並列回路と抵抗の直列接続となる。回路図に描くとということになる。第二Foster展開は逆に単純にアドミッタンスの総和へ部分分数展開すればよく $\begin{eqnarray}<br />Y_2(s)&=&\frac{1}{Z_2(s)}\\<br />&=&\frac{\left(s+2\right)\left(s+4\right)}{s\left(s+3\right)\left(s+5\right)}\\<br />&=&\frac{H_0}{s}+\frac{H_1}{s+3}+\frac{H_2}{s+5}\\<br />&=&\frac{1}{L_0 s}+\frac{1}{L_1 s+R_1}+\frac{1}{L_2 s+R_2}\\<br />L_0&=&\frac{1}{H_0}=\frac{15}{8}\,[H]\\<br />L_1&=&\frac{1}{H_1}=6\,[H]\\<br />R_1&=&\frac{3}{H_1}=18\,[\Omega]\\<br />L_2&=&\frac{1}{H_2}=\frac{10}{3}\,[H]\\<br />R_2&=&\frac{5}{H_2}=\frac{50}{3}\,[\Omega]\\<br />H_0&=&\lim_{s\to0}sY_2(s)\\<br />&=&\left.\frac{\left(s+2\right)\left(s+4\right)}{\left(s+3\right)\left(s+5\right)}\right\|_{s=0}\\<br />&=&\frac{\left(0+2\right)\left(0+4\right)}{\left(0+3\right)\left(0+5\right)}\\<br />&=&\frac{8}{15}\\<br />H_1&=&\lim_{s\to-3}\left(s+3\right)Y_2(s)\\<br />&=&\left.\frac{\left(s+2\right)\left(s+4\right)}{s\left(s+5\right)}\right\|_{s=-3}<br />&=&\frac{\left(-3+2\right)\left(-3+4\right)}{-3\left(-3+5\right)}\\<br />&=&\frac{1}{6}\\<br />H_2&=&\lim_{s\to-5}\left(s+5\right)Y_2(s)\\<br />&=&\left.\frac{\left(s+2\right)\left(s+4\right)}{s\left(s+3\right)}\right\|_{s=-5}\\<br />&=&\frac{\left(-5+2\right)\left(-5+4\right)}{-5\left(-5+3\right)}\\<br />&=&\frac{3}{10}<br />\end{eqnarray}$ ということで２つのRL直列回路とLとの並列接続で構成される。回路図に描くとということになる。

webadm	投稿日時: 2010-4-24 20:47
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【24】アドミッタンス関数今度は趣向が変わった問題。以下の様なRLC回路と等価なRC回路を実現するためのCの値の条件と等価回路を示せというもの。この回路はLとCを含むためωによって誘導性と容量性のどちらかのリアクタンスを持つ。題意の等価なRC回路というのはω≠0で容量性リアクタンスのみを持つようにするという意味になる。従って与えられた元のRLC回路がすべてのωに関して容量性リアクタンスのみ持つようになるCの条件を求めれば良いことになる。問題の回路のサセプタンスが常に容量性になるには $\begin{eqnarray}<br />B(\omega)&=&Im\left(Y(j\omega)\right)\\<br />&=&Im\left(\frac{1}{R_0}+j C_\infty \omega+\frac{1}{j L_1 \omega+R_1}+\frac{1}{R_2-j\frac{1}{C \omega}}\right)\\<br />&=&Im\left(\frac{1}{R_0}+j C_\infty \omega+\frac{R_1-j L_1 \omega}{{L_1}^2 {\omega}^2+{R_1}^2}+\frac{R_2+j\frac{1}{C \omega}}{{R_2}^2+\frac{1}{C^2 {\omega}^2}}\right)\\<br />&=&C_\infty \omega-\frac{L_1 \omega}{{L_1}^2 {\omega}^2+{R_1}^2}+\frac{\frac{1}{C \omega}}{{R_2}^2+\frac{1}{C^2 {\omega}^2}}\\<br />&=&\omega\left(C_\infty-\frac{L_1}{{L_1}^2 {\omega}^2+{R_1}^2}+\frac{C}{C^2 {R_2}^2{\omega}^2+1}\right)\\<br />&=&\omega\left(C_\infty+\frac{\left({L_1}^2 {\omega}^2+{R_1}^2\right)C-\left(C^2 {R_2}^2{\omega}^2+1\right)L_1 }{\left({L_1}^2 {\omega}^2+{R_1}^2\right)\left(C^2 {R_2}^2{\omega}^2+1\right)}\right)\\<br />&=&\omega\left(C_\infty+\frac{C L_1\left({L_1} - C {R_2}^2\right){\omega}^2+\left(C{R_1}^2-L_1\right)}{\left({L_1}^2 {\omega}^2+{R_1}^2\right)\left(C^2 {R_2}^2{\omega}^2+1\right)}\right)\ge0\,\forall\omega<br />\end{eqnarray}$ を満たす必要がある。すなわちCの値が $\begin{eqnarray}<br />{L_1} - C {R_2}^2&\ge&0<br />C{R_1}^2-L_1&\ge&0<br />\end{eqnarray}$ を同時に満たす必要がある。整理して与えられた定数を代入すると $\begin{eqnarray}<br />\frac{L_1}{{R_2}^2}\ge &C& \ge \frac{L_1}{{R_1}^2}\\<br />24 \ge &C& \ge \frac{2}{3}<br />\end{eqnarray}$ こっからどうすんだ。見通しが悪かった。どうやら著者の判りにくい解答を理解すると題意を読み違えていたようだ。角周波数領域だけで物事を考えていたのが間違いで、複素角周波数領域で考えないといけなかった。従って回路からアドミッタンス関数を起こすと $\begin{eqnarray}<br />Y(s)&=&\frac{1}{R_0}+C_\infty s+\frac{1}{L_1 s+R_1}+\frac{1}{R_2+\frac{1}{C s}}\\<br />&=&\frac{1}{R_0}+C_\infty s+\frac{\frac{1}{L_1}}{s+\frac{R_1}{L_1}}+\frac{\frac{ s}{R_2}}{s+\frac{1}{C R_2}}<br />\end{eqnarray}$ この関数はs=-R1/L1,-1/C*R2,∞の３つの極を持つことになる。従ってRL直列回路とRC直列回路にそれぞれが独立した極を持つので三種類の素子が必要になってしまう。問題の趣旨は、RL直列回路とRC直列回路が同一の極（重根）をもつようにし、なおかつ全体的に容量性（留数が負）になるようにせよということだった。重根を持たせるにはCの値を $\begin{eqnarray}<br />\frac{R_1}{L_1}&=& \frac{1}{C R_2}\\<br />C&=&\frac{L_1}{R_1 R_2}\\<br />&=&\frac{6}{3\times \frac{1}{2}}=4\,[F]<br />\end{eqnarray}$ とすればよい。さてあとはRC回路のみでどう実現されるかだが、見通しができていない(´д` ) 実は良く判ってなかったのである。ちなみにC=8として問題の回路のサセプタンス値を3Dでプロットしてみるとs=-0.25とs=-0.5に極が現れているのが確認できる。前者は容量性サセプタンス項、後者は誘導性サセプタンス項のもの。両者は互いに山と谷の極性が逆方向なのと留数の絶対値が容量性の方が勝っているので容量性側の起伏が大きい、Cの値を変更して容量性の極を誘導性の極の上に重ねると誘導性は消滅し、容量性のみが残ると予想される。C=4にすると双方の極がs=-0.5で重なる。見事に誘導性の痕跡は消え失せて容量性の極だけが残っている。著者の解答にある負の留数ってなんだという疑問が沸く。回路から起こしたアドミッタンス関数の式には負の留数などないように見える。しかしRC直列回路のアドミッタンス項は分子と分母の次数が同じなので以下の様に更に部分分数展開できることに気づくべきだった。 $\begin{eqnarray}<br />Y(s)&=&\frac{1}{R_0}+C_\infty s+\frac{\frac{1}{L_1}}{s+\frac{R_1}{L_1}}+\frac{\frac{ s}{R_2}}{s+\frac{1}{C R_2}}\\<br />&=&\frac{1}{R_0}+C_\infty s+\frac{\frac{1}{L_1}}{s+\frac{R_1}{L_1}}+\frac{1}{R_2}-\frac{\frac{1}{C {R_2}^2}}{s+\frac{1}{C R_2}}<br />\end{eqnarray}$ 確かに負の留数が現れる。そこで先ほど導いたCの値を代入して容量性になるように数式を操作してみると $\begin{eqnarray}<br />Y(s)&=&\frac{1}{R_0}+C_\infty s+\frac{\frac{1}{L_1}}{s+\frac{R_1}{L_1}}+\frac{1}{R_2}-\frac{\frac{1}{C {R_2}^2}}{s+\frac{1}{C R_2}}\\<br />&=&\frac{1}{R_0}+C_\infty s+\frac{1}{R_2}-\frac{\frac{R_1}{L_1 {R_2}}-\frac{1}{L_1 }}{s+\frac{R_1}{L_1 }}\\<br />&=&\frac{1}{R_0}+C_\infty s+\frac{1}{R_2}-\frac{\frac{1}{L_1}\left(\frac{R_1}{{R_2}}-1\right)}{s+\frac{R_1}{L_1 }}\\<br />&=&\frac{1}{R_0}+C_\infty s+\frac{1}{R_2}-\frac{\frac{R_1}{L_1}\left(\frac{1}{{R_2}}-\frac{1}{R_1}\right)}{s+\frac{R_1}{L_1 }}\\<br />&=&\frac{1}{R_0}+C_\infty s+\frac{1}{R_2}-\left(\frac{1}{R_2}-\frac{1}{R_1}\right)+\left(\left(\frac{1}{R_2}-\frac{1}{R_1}\right)-\frac{\frac{R_1}{L_1}\left(\frac{1}{{R_2}}-\frac{1}{R_1}\right)}{s+\frac{R_1}{L_1 }}\right)\\<br />&=&\frac{1}{R_0}+C_\infty s+\frac{1}{R_1}+\frac{\left(\frac{1}{R_2}-\frac{1}{R_1}\right)s}{s+\frac{R_1}{L_1 }}\\<br />&=&\frac{1}{R_0}+C_\infty s+\frac{1}{R_1}+\frac{\frac{R_1-R_2}{R_1 R_2}s}{s+\frac{R_1}{L_1 }}\\<br />&=&\frac{R_0+R_1}{R_0 R_1}+C_\infty s+\frac{1}{\frac{R_1 R_2}{R_1-R_2}+\frac{R_1^2 R_2}{L_1\left(R_1-R_2\right)s}}\\<br />&=&\frac{1}{{R_0}^\'}+C_\infty s+\frac{1}{{R_1}^\'+\frac{1}{{C_1}^\' s}}\\<br />R_0&=&4\,[\Omega]\\<br />C_\infty&=&3\,[F]\\<br />R_1&=&3\,[\Omega]\\<br />L_1&=&6\,[H]\\<br />R_2&=&\frac{1}{2}\,[\Omega]\\<br />{R_0}^\'&=&\frac{R_0 R_1}{R_0+R_1}=\frac{4\times 3}{4+3}=\frac{12}{7}\,[\Omega]\\<br />{R_1}^\'&=&\frac{R_1 R_2}{R_1-R_2}=\frac{3\times \frac{1}{2}}{3-\frac{1}{2}}=\frac{3}{5}\,[\Omega]\\<br />{C_1}^\'&=&\frac{L_1\left(R_1-R_2\right)}{R_1^2 R_2}=\frac{6\left(3-\frac{1}{2}\right)}{3^2\times \frac{1}{2}}=\frac{10}{3}\,[F]<br />\end{eqnarray}$ ということになる。回路図で表すとというわけでRC回路で実現できる。やっとわかったよﾏﾏﾝ(ﾉ∀`) 上記の方法以外にも、極がs=-R1/L1,∞のみとなるCの値を元のアドミッタンス関数に代入してs=0、s=-R1/L1に関する留数(H0,H1)を求めれば手品的な計算無しで同じ結果が得られると思われる。それは簡単なので読者の課題としよう(´∀` ) と思ったけどせっかくなので以下に別解を示すことにしよう。 $\begin{eqnarray}<br />Y(s)&=&\frac{1}{R_0}+C_\infty s+\frac{\frac{1}{L_1}}{s+\frac{R_1}{L_1}}+\frac{1}{R_2}-\frac{\frac{R_1}{L_1 {R_2}}}{s+\frac{R_1}{L_1}}\\<br />&=&H_0+H_\infty s+\frac{H_1 s}{s+\frac{R_1}{L_1}}\\<br />&=&\frac{1}{{R_0}^\'}+C_\infty s+\frac{1}{{R_1}^\'+\frac{1}{{C_1}^\' s}}\\<br />R_0&=&4\,[\Omega]\\<br />C_\infty&=&3\,[F]\\<br />R_1&=&3\,[\Omega]\\<br />L_1&=&6\,[H]\\<br />R_2&=&\frac{1}{2}\,[\Omega]\\<br />{R_0}^\'&=&\frac{1}{H_0}\\<br />&=&\frac{R_0 R_1}{R_0+R_1}=\frac{4\times 3}{4+3}\\<br />&=&\frac{12}{7}\,[\Omega]\\<br />{R_1}^\'&=&\frac{1}{H_1}=\frac{R_1 R_2}{R_1-R_2}\\<br />&=&\frac{3\times \frac{1}{2}}{3-\frac{1}{2}}\\<br />&=&\frac{3}{5}\,[\Omega]\\<br />{C_1}^\'&=&\frac{H_1}{\frac{R_1}{L_1}}\\<br />&=&\frac{\frac{R_1-R_2}{R_1 R_2}}{\frac{R_1}{L_1}}\\<br />&=&\frac{L_1\left(R_1-R_2\right)}{{R_1}^2 R_2}\\<br />&=&\frac{6\left(3-\frac{1}{2}\right)}{{3}^2\times \frac{1}{2}}\\<br />&=&\frac{10}{3}\,[F]\\<br />H_0&=&\lim_{s\to0}Y(s)\\<br />&=&\left.\frac{1}{R_0}+C_\infty s+\frac{\frac{1}{L_1}}{s+\frac{R_1}{L_1}}+\frac{1}{R_2}-\frac{\frac{R_1}{L_1 {R_2}}}{s+\frac{R_1}{L_1}}\right\|_{s=0}\\<br />&=&\frac{1}{R_0}+\frac{1}{R_1 }+\cancel{\frac{1}{R_2}}-\cancel{\frac{1}{R_2}}\\<br />&=&\frac{R_0+R_1}{R_0 R_1}\\<br />H_1&=&\lim_{s\to-\frac{R_1}{L_1}}\frac{\left(s+\frac{R_1}{L_1}\right)Y(s)}{s}\\<br />&=&\left.\frac{\frac{1}{L_1}}{s}-\frac{\frac{R_1}{L_1 {R_2}}}{s}\right\|_{s=-\frac{R_1}{L_1}}\\<br />&=&\frac{\frac{1}{L_1}}{-\frac{R_1}{L_1}}-\frac{\frac{R_1}{L_1 {R_2}}}{-\frac{R_1}{L_1}}\\<br />&=&\frac{1}{R_2}-\frac{1}{R_1}\\<br />&=&\frac{R_1-R_2}{R_1 R_2}<br />\end{eqnarray}$ なんだ簡単じゃないか(´∀` )

webadm	投稿日時: 2010-4-27 10:19
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【25】続：アドミッタンス関数勝手に題名を付けているが、たぶんアドミッタンス関数で考えた方が易しいのではと。ある回路と並列に抵抗R=3[Ω]を接続したときのインピーダンス関数が以下の通り既知である場合、元の回路のインピーダンス関数を求めよというもの。 $\frac{9s^2+15}{s^3+3s^2+4s+5}$ 並列接続回路なのでアドミッタンス関数として考えよう。元の回路のアドミッタンス関数をY0とすると、抵抗を並列に接続した後のアドミッタンス関数をYとする。その場合、以下の関係が成り立つ。 $\begin{eqnarray}<br />Y(s)&=&Y_0(s)+\frac{1}{R}\\<br />&=&Y_0(s)+\frac{1}{3}\\<br />&=&\frac{s^3+3s^2+4s+5}{9s^2+15}<br />\end{eqnarray}$ 従って元のインピーダンス関数をZ0とすると $\begin{eqnarray}<br />Z_0(s)&=&\frac{1}{Y_0(s)}\\<br />&=&\frac{1}{\Large\frac{s^3+3s^2+4s+5}{9s^2+15}-\frac{1}{3}}\\<br />&=&\frac{1}{\Large\frac{3\left(s^3+3s^2+4s+5\right)-\left(9s^2+15\right)}{3\left(9s^2+15\right)}}\\<br />&=&\frac{\left(9s^2+15\right)}{\left(s^3+\cancel{3s^2}+4s+\cancel{5}\right)-\left(\cancel{3s^2}+\cancel{5}\right)}\\<br />&=&\frac{9s^2+15}{s\left(s^2+4\right)}\\<br />&=&\frac{H_0}{s}+\frac{H_1 s}{s^2+4}\\<br />&=&\frac{1}{C_0 s}+\frac{1}{C_1 s+\frac{1}{L_1 s}}\\<br />C_0&=&\frac{1}{H_0}=\frac{4}{15}\,[F]\\<br />C_1&=&\frac{1}{H_1}=\frac{4}{21}\,[F]\\<br />L_1&=&\frac{H_1}{4}=\frac{21}{16}\,[H]\\<br />H_0&=&\lim_{s\to0}s Z_0(s)\\<br />&=&\left.\frac{9s^2+15}{\left(s^2+4\right)}\right\|_{s=0}\\<br />&=&\frac{15}{4}\\<br />H_1&=&\lim_{s^2=-4}\frac{\left(s^2+4\right)Z_0(s)}{s}\\<br />&=&\left.\frac{9s^2+15}{s^2}\right\|_{s^2=-4}\\<br />&=&\frac{9\left(-4\right)+15}{-4}\\<br />&=&\frac{21}{4}<br />\end{eqnarray}$ ということになる。回路図に描くとということになる。

webadm	投稿日時: 2010-4-28 9:20
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【26】密結合変成器の分離次ぎは相互インダクタンスを伴うリアクタンス回路に関する問題。以下の回路の相互インダクタンスの結合係数kが1である場合、この回路に等価な相互インダクタンスを含まないLC回路を求めよというもの。この種の操作は密結合変成器の分離と呼ばれ変成器を伴わない二端子回路の構成法。結合係数は $k=M/sqrt{L_1 L_2}$ で定義されていたことを思い出そう。問題の回路は以下の様な等価回路に置き換えることができる。これより駆動点インピーダンスの式を起こすと $\begin{eqnarray}<br />Z(s)&=&\frac{1}{C_1 s}+\left(L_1-M\right)s+\frac{1}{\Large\frac{1}{M s+\frac{1}{C_2 s}}+\frac{1}{\left(L_2-M\right)s+\frac{1}{C_3 s}}}\\<br />&=&\frac{C_1\left(L_1-M\right)s^2+1}{C_1 s}+\frac{1}{\Large\frac{\frac{1}{M} s}{s^2+\frac{1}{C_2 M}}+\frac{\frac{1}{L_2-M}s}{s^2+\frac{1}{C_3\left(L_2-M\right)}}}\\<br />&=&\frac{\left(L_1-M\right)\left(s^2+\frac{1}{C_1\left(L_1-M\right)}\right)}{s}+\frac{\left(s^2+\frac{1}{C_2 M}\right)\left(s^2+\frac{1}{C_3\left(L_2-M\right)}\right)}{\left(s^2+\frac{1}{C_3\left(L_2-M\right)}\right)\frac{1}{M} s+\left(s^2+\frac{1}{C_2 M}\right)\frac{1}{L_2-M}s}\\<br />&=&\frac{\left(L_1-M\right)\left(s^2+\frac{1}{C_1\left(L_1-M\right)}\right)}{s}+\frac{\left(s^2+\frac{1}{C_2 M}\right)\left(s^2+\frac{1}{C_3\left(L_2-M\right)}\right)}{s\left(\frac{L_2}{M\left(L_2-M\right)}s^2+\frac{C_2+C_3}{C_2 C_3 M\left(L_2-M\right)}\right)}\\<br />&=&\frac{\left(L_1-M\right)\left(s^2+\frac{1}{C_1\left(L_1-M\right)}\right)}{s}+\frac{\frac{M\left(L_2-M\right)}{L_2}\left(s^2+\frac{1}{C_2 M}\right)\left(s^2+\frac{1}{C_3\left(L_2-M\right)}\right)}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\left(L_1-M\right)\left(s^2+\frac{1}{C_1\left(L_1-M\right)}\right)\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)+\frac{M\left(L_2-M\right)}{L_2}\left(s^2+\frac{1}{C_2 M}\right)\left(s^2+\frac{1}{C_3\left(L_2-M\right)}\right)}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\left(L_1-M\right)\left(s^4+\frac{L_2 C_2 C_3+C_1\left(L_1-M\right)\left(C_2+C_3\right)}{C_1\left(L_1-M\right)L_2 C_2 C_3}s^2+\frac{C_2+C_3}{C_1\left(L_1-M\right)L_2 C_2 C_3}\right)+\frac{M\left(L_2-M\right)}{L_2}\left(s^4+\frac{C_3\left(L_2-M\right)+C_2 M}{C_2 C_3 M\left(L_2-M\right)}s^2+\frac{1}{C_2 C_3 M\left(L_2-M\right)}\right)}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\left(\left(L_1-M\right)s^4+\frac{L_2 C_2 C_3+C_1\left(L_1-M\right)\left(C_2+C_3\right)}{C_1 L_2 C_2 C_3}s^2+\frac{C_2+C_3}{C_1 L_2 C_2 C_3}\right)+\left(\frac{M\left(L_2-M\right)}{L_2}s^4+\frac{C_3\left(L_2-M\right)+C_2 M}{L_2 C_2 C_3}s^2+\frac{1}{L_2 C_2 C_3}\right)}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\frac{L_1 L_2 -M^2}{L_2}s^4+\frac{L_2 C_2 C_3+C_1\left(L_1-M\right)\left(C_2+C_3\right)+C_1\left(C_3\left(L_2-M\right)+C_2 M\right)}{C_1 L_2 C_2 C_3}s^2+\frac{C_1+C_2+C_3}{C_1 L_2 C_2 C_3}}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\frac{L_1 L_2 -M^2}{L_2}s^4+\frac{L_2 C_2 C_3+L_1 C_1 C_2+L_1 C_1 C_3+L_2 C_1 C_3 -2 M C_1 C_3}{C_1 L_2 C_2 C_3}s^2+\frac{C_1+C_2+C_3}{C_1 L_2 C_2 C_3}}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />\end{eqnarray}$ ここで題意よりk=1であることから $L_1 L_2-M^2=0$ ということになり、式は以下の様になり題意より定数を代入すると。 $\begin{eqnarray}<br />Z(s)&=&\frac{\frac{L_2 C_2 C_3+L_1 C_1 C_2+L_1 C_1 C_3+L_2 C_1 C_3 -2 M C_1 C_3}{C_1 L_2 C_2 C_3}s^2+\frac{C_1+C_2+C_3}{C_1 L_2 C_2 C_3}}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\frac{8\times 1\times 1+2\times 2\times 1+2\times 2\times 1+8\times 2\times 1 -2 \sqrt{2\times 8}\times 2\times 1}{2\times 8\times 1\times 1}s^2+\frac{2+1+1}{2\times 8\times 1\times 1}}{s\left(s^2+\frac{1+1}{8\times 1\times 1}\right)}\\<br />&=&\frac{s^2+\frac{1}{4}}{s\left(s^2+\frac{1}{4}\right)}\\<br />&=&\frac{1}{s}\\<br />&=&\frac{1}{C s}\\<br />C&=&1\,[F]<br />\end{eqnarray}$ ということでただ一個のキャパシタンスと等価になる。一方で相互インダクタンスのもうひとつの等価回路について調べるとこれより駆動点インピーダンスの式を起こすと $\begin{eqnarray}<br />Z(s)&=&\frac{1}{C_1 s}+\left(L_1+M\right)s+\frac{1}{\Large\frac{1}{-M s+\frac{1}{C_2 s}}+\frac{1}{\left(L_2+M\right)s+\frac{1}{C_3 s}}}\\<br />&=&\frac{C_1\left(L_1+M\right)s^2+1}{C_1 s}+\frac{1}{\Large-\frac{\frac{1}{M} s}{s^2-\frac{1}{C_2 M}}+\frac{\frac{1}{L_2+M}s}{s^2+\frac{1}{C_3\left(L_2+M\right)}}}\\<br />&=&\frac{\left(L_1+M\right)\left(s^2+\frac{1}{C_1\left(L_1+M\right)}\right)}{s}+\frac{\left(s^2-\frac{1}{C_2 M}\right)\left(s^2+\frac{1}{C_3\left(L_2+M\right)}\right)}{-\left(s^2+\frac{1}{C_3\left(L_2+M\right)}\right)\frac{1}{M} s+\left(s^2-\frac{1}{C_2 M}\right)\frac{1}{L_2+M}s}\\<br />&=&\frac{\left(L_1+M\right)\left(s^2+\frac{1}{C_1\left(L_1+M\right)}\right)}{s}-\frac{\left(s^2-\frac{1}{C_2 M}\right)\left(s^2+\frac{1}{C_3\left(L_2+M\right)}\right)}{s\left(\frac{L_2}{M\left(L_2+M\right)}s^2+\frac{C_2+C_3}{C_2 C_3 M\left(L_2-M\right)}\right)}\\<br />&=&\frac{\left(L_1+M\right)\left(s^2+\frac{1}{C_1\left(L_1+M\right)}\right)}{s}-\frac{\frac{M\left(L_2+M\right)}{L_2}\left(s^2-\frac{1}{C_2 M}\right)\left(s^2+\frac{1}{C_3\left(L_2+M\right)}\right)}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\left(L_1+M\right)\left(s^2+\frac{1}{C_1\left(L_1+M\right)}\right)\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)-\frac{M\left(L_2+M\right)}{L_2}\left(s^2-\frac{1}{C_2 M}\right)\left(s^2+\frac{1}{C_3\left(L_2+M\right)}\right)}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\left(L_1+M\right)\left(s^4+\frac{L_2 C_2 C_3+C_1\left(L_1+M\right)\left(C_2+C_3\right)}{C_1\left(L_1+M\right)L_2 C_2 C_3}s^2+\frac{C_2+C_3}{C_1\left(L_1+M\right)L_2 C_2 C_3}\right)-\frac{M\left(L_2+M\right)}{L_2}\left(s^4-\frac{C_3\left(L_2-M\right)-C_2 M}{C_2 C_3 M\left(L_2+M\right)}s^2-\frac{1}{C_2 C_3 M\left(L_2+M\right)}\right)}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\left(\left(L_1+M\right)s^4+\frac{L_2 C_2 C_3+C_1\left(L_1+M\right)\left(C_2+C_3\right)}{C_1 L_2 C_2 C_3}s^2+\frac{C_2+C_3}{C_1 L_2 C_2 C_3}\right)-\left(\frac{M\left(L_2+M\right)}{L_2}s^4-\frac{C_3\left(L_2+M\right)-C_2 M}{L_2 C_2 C_3}s^2-\frac{1}{L_2 C_2 C_3}\right)}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\frac{L_1 L_2 -M^2}{L_2}s^4+\frac{L_2 C_2 C_3+C_1\left(L_1+M\right)\left(C_2+C_3\right)+C_1\left(C_3\left(L_2+M\right)-C_2 M\right)}{C_1 L_2 C_2 C_3}s^2+\frac{C_1+C_2+C_3}{C_1 L_2 C_2 C_3}}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\frac{L_1 L_2 -M^2}{L_2}s^4+\frac{L_2 C_2 C_3+L_1 C_1 C_2+L_1 C_1 C_3+L_2 C_1 C_3 +2 M C_1 C_3}{C_1 L_2 C_2 C_3}s^2+\frac{C_1+C_2+C_3}{C_1 L_2 C_2 C_3}}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />\end{eqnarray}$ 一カ所だけ符号が異なるだけである。同様にk=1の時は分子の４次の項は消滅するので、定数を代入すると $\begin{eqnarray}<br />Z(s)&=&\frac{\frac{L_2 C_2 C_3+L_1 C_1 C_2+L_1 C_1 C_3+L_2 C_1 C_3 +2 M C_1 C_3}{C_1 L_2 C_2 C_3}s^2+\frac{C_1+C_2+C_3}{C_1 L_2 C_2 C_3}}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\frac{8\times 1\times 1+2\times 2\times 1+2\times 2\times 1+8\times 2\times 1 +2 \sqrt{2\times 8}\times 2\times 1}{2\times 8\times 1\times 1}s^2+\frac{2+1+1}{2\times 8\times 1\times 1}}{s\left(s^2+\frac{1+1}{8\times 1\times 1}\right)}\\<br />&=&\frac{3s^2+\frac{1}{4}}{s\left(s^2+\frac{1}{4}\right)}\\<br />&=&\frac{3\left(s^2+\frac{1}{12}\right)}{s\left(s^2+\frac{1}{4}\right)}\\<br />&=&\frac{H_0}{s}+\frac{H_1 s}{s^2+\frac{1}{4}}\\<br />&=&\frac{1}{C s}+\frac{1}{{C_1}^\'s+\frac{1}{L_1 s}}\\<br />C&=&\frac{1}{H_0}=1\,[F]<br />{C_1}^\'&=&\frac{1}{H_1}=\frac{1}{2}\,[F]\\<br />L_1&=&4 H_1=8\,[H]\\<br />H_0&=&\lim_{s\to0}s Z(s)\\<br />&=&\left.\frac{3\left(s^2+\frac{1}{12}\right)}{\left(s^2+\frac{1}{4}\right)}\right\|_{s=0}\\<br />&=&\frac{3\left(\frac{1}{12}\right)}{\left(\frac{1}{4}\right)}\\<br />&=&1<br />H_1&=&\lim_{s\to-\frac{1}{4}}\frac{\left(s^2+\frac{1}{4}\right)Z(s)}{s}\\<br />&=&\left.\frac{3\left(s^2+\frac{1}{12}\right)}{s^2}\right\|_{s=\frac{1}{4}}\\<br />&=&\frac{3\left(-\frac{1}{4}+\frac{1}{12}\right)}{-\frac{1}{4}}\\<br />&=&2<br />\end{eqnarray}$ ということになる。回路図に描くとといことになる。

webadm	投稿日時: 2010-4-29 19:35
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【27】逆回路ふう残すところあと7問。ここからしばらく逆回路の問題。以下の回路の逆回路を求めよというもの。この回路は駆動点インピーダンス関数で表すと $Z_1(s)=L_0 s$ s=0に零点、s=∞に極を持ちスケーリングファクタはL0ということになる。したがって逆回路の駆動点インピーダンス関数はs=0に極、s=∞に零点を持ちスケーリングファクタが1/L0に比例する。 $begin{eqnarray}<br />{Y_1}^\'(s)&=&Z_1(s)<br />&=&L_0 s\\<br />&=&C_0 s\\<br />C_0&=&L_0<br />\end{eqnarray}$ ということになる。回路図上ではLの双対であるCに置き換わることになる。従って逆回路の回路はとなる。次はLC直列回路駆動点インピーダンス関数は $\begin{eqnarray}<br />{Z_2}(s)&=&L_1 s+\frac{1}{C_2 s}<br />\end{eqnarray}$ 従って逆回路は $\begin{eqnarray}<br />{Y_2}^\'(s)&=&Z_2(s)\\<br />&=&L_1 s+\frac{1}{C_2 s}\\<br />&=&C_1 s+\frac{1}{L_2 s}<br />C_1&=&L_1\\<br />L_2&=&C_2<br />\end{eqnarray}$ 回路図的にはLがCへCがLへ、直列接続が並列接続に変わる。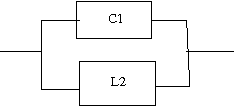次はLとLC並列回路の直列接続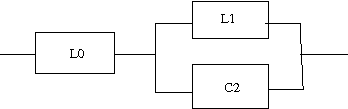駆動点インピーダンス関数は $\begin{eqnarray}<br />Z_3(s)&=&L_0 s+\frac{1}{L_1 s+\frac{1}{C_2 s}}<br />\end{eqnarray}$ 従って逆回路は $\begin{eqnarray}<br />{Y_3}^\'(s)&=&Z_3(s)\\<br />&=&L_0 s+\frac{1}{L_1 s+\frac{1}{C_2 s}}\\<br />&=&C_0 s+\frac{1}{C_1 s+\frac{1}{L_2 s}}\\<br />C_0&=&L_0\\<br />C_1&=&L_1\\<br />L_2&=&C_2<br />\end{eqnarray}$ 従ってCとLC直列回路の並列接続となる。回路図に描くと 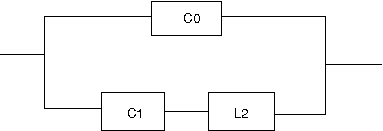s=0,∞以外にも複数の特異点を持つ場合、同じ回路が複数形存在することはFoster展開やCauer展開で学んだとおり。元の回路のインピーダンスは逆回路のアドミッタンスとなる点を利用すれば最も簡単に双対となる回路を導くことができる。次は２つのLC並列回路の直列接続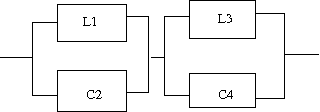関数で表すと $\begin{eqnarray}<br />Z_4(s)&=&\frac{1}{\frac{1}{L_1 s}+C_2 s}+\frac{1}{\frac{1}{L_3 s}+C_4 s}<br />\end{eqnarray}$ 従って逆回路の関数は $\begin{eqnarray}<br />{Y_4}^\'&=&Z_4(s)\\<br />&=&\frac{1}{\frac{1}{L_1 s}+C_2 s}+\frac{1}{\frac{1}{L_3 s}+C_4 s}\\<br />&=&\frac{1}{\frac{1}{C_1 s}+L_2 s}+\frac{1}{\frac{1}{C_3 s}+L_4 s}\\<br />C_1&=&L_1\\<br />L_2&=&C_2\\<br />C_3&=&L_3\\<br />L_4&=&C_4<br />\end{eqnarray}$ ２つのLC直列回路の並列接続となる。回路図で表すと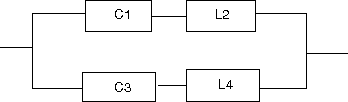最後はLとLC並列回路とCの直列接続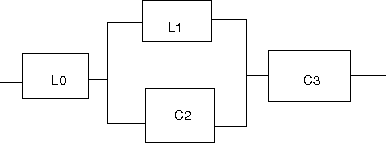駆動点インピーダンス関数は $\begin{eqnarray}<br />Z_5(s)&=&L_0 s+\frac{1}{\frac{1}{L_1 s}+C_2 s}+\frac{1}{C_3 s}<br />\end{eqnarray}$ 従って逆回路は $\begin{eqnarray}<br />{Y_5}^\'&=&Z_5(s)\\<br />&=&L_0 s+\frac{1}{\frac{1}{L_1 s}+C_2 s}+\frac{1}{C_3 s}\\<br />&=&C_0 s+\frac{1}{\frac{1}{C_1 s}+L_2 s}+\frac{1}{L_3 s}\\<br />C_0&=&L_0\\<br />C_1&=&L_1\\<br />L_2&=&C_2\\<br />L_3&=&C_3<br />\end{eqnarray}$ 従ってCとLC直列回路とLの並列接続となる。回路図に描くと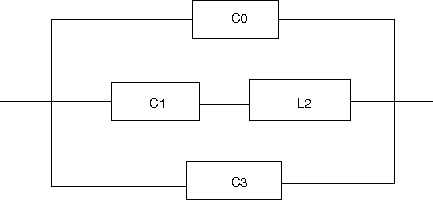ということになる。

webadm	投稿日時: 2010-4-30 9:49
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【28】続：逆回路次も逆回路。今度は与えられた回路のR=100に対する逆回路を求める問題。 Rに対する逆回路とはZ1とZ2が互いに逆回路の場合に $Z_1 Z_2=R^2$ が成り立つものを言う。Rは定数である。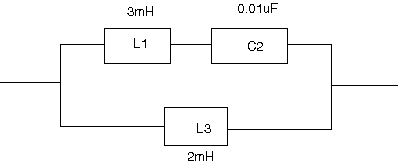駆動点インピーダンス関数を回路から起こすと $\begin{eqnarray}<br />Z_1(s)&=&\frac{1}{\frac{1}{L_1 s+\frac{1}{C_2 s}}+\frac{1}{L_3 s}}<br />\end{eqnarray}$ 従って逆回路は $\begin{eqnarray}<br />Y_2&=&\frac{1}{R^2}Z_1(s)\\<br />&=&\frac{1}{R^2}\frac{1}{\frac{1}{L_1 s+\frac{1}{C_2 s}}+\frac{1}{L_3 s}}\\<br />&=&\frac{1}{\frac{1}{C_1 s+\frac{1}{L_2 s}}+\frac{1}{C_3 s}}\\<br />C_1&=&\frac{L_1}{R^2}=\frac{3\times10^{-3}}{100^2}\\<br />&=&0.3\,[\mu F]\\<br />L_2&=&C_2 R^2=0.01\times10^{-6}\times100^2\\<br />&=&0.1\,[mH]\\<br />C_3&=&\frac{L_3}{R^2}=\frac{2\times10^{-3}}{100^2}\\<br />&=&0.2\,[\mu F]\\<br />\end{eqnarray}$ ということでLC並列回路とCの直列接続となる。回路図で表すと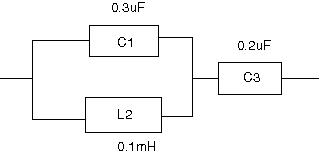ということになる。

webadm	投稿日時: 2010-4-30 10:15
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【29】続々：逆回路次は逆回路の最後の問題。 Z1,Z2が互いにRに対する逆回路である場合に、以下の回路が定抵抗回路となることを示せというもの。駆動点インピーダンスはR^2=Z1Z2なる関係が成り立つ場合 $\begin{eqnarray}<br />Z(s)&=&\frac{1}{\frac{1}{R}+\frac{1}{Z_1}}+\frac{1}{\frac{1}{R}+\frac{1}{Z_2}}\\<br />&=&\frac{R Z_1}{R+Z_1}+\frac{R Z_2}{R+Z_2}\\<br />&=&\frac{R Z_1\left(R+Z_2\right)+R Z_2\left(R+Z_1\right)}{\left(R+Z_1\right)\left(R+Z_2\right)}\\<br />&=&\frac{R\left(R \left(Z_1+Z_2\right)+2 Z_1 Z_2\right)}{R^2+\left(Z_1+Z_2\right)R+Z_1 Z_2}\\<br />&=&\frac{R^2\left(\left(Z_1+Z_2\right)+2 R\right)}{R\left(2R+\left(Z_1+Z_2\right)\right)}\\<br />&=&R<br />\end{eqnarray}$ となり定抵抗回路となる。もう一方の回路についても同様に 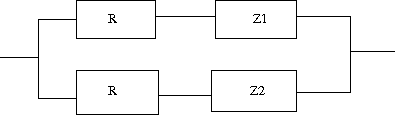R^2=Z1Z2が成り立つとすると駆動点インピーダンスは $\begin{eqnarray}<br />Z(s)&=&\frac{1}{\frac{1}{R+Z_1}+\frac{1}{R+Z_2}}\\<br />&=&\frac{\left(R+Z_1\right)\left(R+Z_2\right)}{2R+Z_1+Z_2}\\<br />&=&\frac{R^2+\left(Z_1+Z_2\right)R+Z_1 Z_2}{2R+Z_1+Z_2}\\<br />&=&\frac{R\left(2R+Z_1+Z_2\right)}{2R+Z_1+Z_2}\\<br />&=&R<br />\end{eqnarray}$ となり定抵抗回路となる。

« 1 2 (3) 4 »

スレッド表示 | 新しいものから

前のトピック | 次のトピック | トップ

投稿するにはまず登録を