Gan's blog - フォーラム

ログイン

パスワード紛失

新規登録

Main Menu

ホーム WordPress フォーラムリンク集投票 FAQ myalbum

Tweet

Facebook

Line

:-?

メイン > > 電気回路理論おもちゃ箱 > 一端子対回路：演習問題

投稿するにはまず登録を

« 1 2 3 (4)

スレッド表示 | 新しいものから

前のトピック | 次のトピック | 下へ

投稿者	スレッド
webadm	投稿日時: 2010-4-30 10:59
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【30】まだまだ：逆回路逆回路の問題は続くよ。次はどちらかというと前問の応用問題。回路をよーく見比べてみよう。２つの回路をいずれもR1の定抵抗回路にしたいが、Z1とZ0をどのような回路にすればよいかという問題。 (a)は前問の最初の回路から、(b)は前問の最後の回路からヒントを得られる。 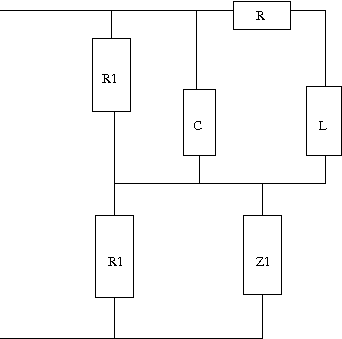(a)のRLC回路部分のインピーダンスをZ2とすると、前問よりZ1とZ2をR1に対する逆回路にすればよいわけで RLC回路部分のインピーダンスZ2はCとRL直列回路の並列接続であるので $\begin{eqnarray}<br />Z_2(s)&=&\frac{1}{C s+\frac{1}{R+L s}}<br />\end{eqnarray}$ 従ってZ1は $\begin{eqnarray}<br />Y_1(s)&=&\frac{1}{{R_1}^2}\frac{1}{C s+\frac{1}{R+L s}}\\<br />&=&\frac{1}{L_1 s+\frac{1}{G+C_1 s}}\\<br />L_1&=&C{R_1}^2\\<br />G_1&=&\frac{R}{{R_1}^2}\\<br />C_1&=&\frac{L}{{R_1}^2}<br />\end{eqnarray}$ となり、LとRC並列回路の直列接続となる。回路図に描くと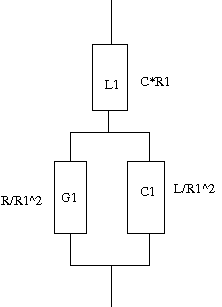ということになる。 (b)の回路についても同様に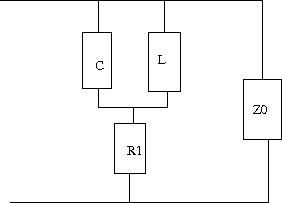前問の最後の設問にある回路と同様にZ0はR1と直列に左のLC並列回路とR1に対する逆回路であれば回路全体がR1の定抵抗回路になることから $begin{eqnarray}<br />Z_0(s)&=&R_1+{R_1}^2\left(C s+\frac{1}{L s}\right)\\<br />&=&R_1+L_0 s +\frac{1}{C_0 s}\\<br />L_0&=&C{R_1}^2\\<br />C_0&=&\frac{L}{{R_1}^2}<br />\end{eqnarray}$ 従ってR1とLとCの直列回路ということになる。回路図に描くと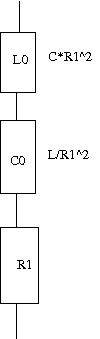ということになる。

webadm	投稿日時: 2010-4-30 12:03
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【31】もうひとつの：逆回路これが最後か逆回路の問題。最後はLattice回路のご登場。この次に学ぶ二端子対回路で本格的に学ぶことになる。 Z1とZ2がRに対して逆回路である場合、定抵抗回路になることを示せというもの。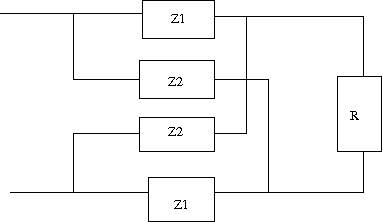さてこの回路の駆動点インピーダンスを求めるにはどうすんだっけ。ブリッジ回路なので簡単に式を立てることはできない。せっかくなので著者の解答とは異なる別解で解いてみよう。まず最初にZ1,Z2,RのΔ結線を等価なY結線に置き換えることによってZb+Z2直列回路とZc+Z1直列回路の並列接続にZaが直列接続された回路となり、駆動点インピーダンスが簡単に立てられるようになる。 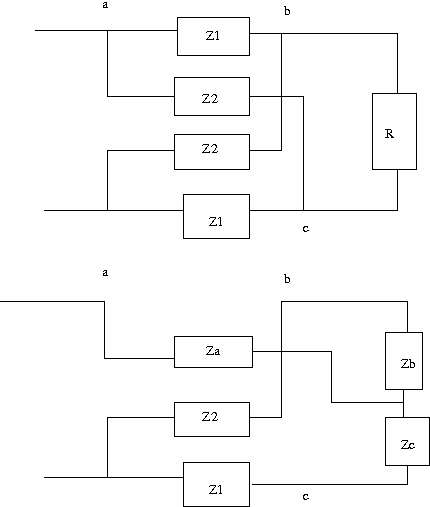$\begin{eqnarray}<br />Z(s)&=&Z_a+\frac{1}{\frac{1}{Z_b+Z_2}+\frac{1}{Z_c+Z_1}}\\<br />&=&Z_a+\frac{\left(Z_b+Z_2\right)\left(Z_c+Z_1\right)}{Z_1+Z_2+Z_b+Z_c}\\<br />&=&\frac{Z_1 Z_2}{Z_1+Z_2+R}+\frac{\left(\frac{Z_1 R}{Z_1+Z_2+R}+Z_2\right)\left(\frac{Z_2 R}{Z_1+Z_2+R}+Z_1\right)}{Z_1+Z_2+\frac{Z_1 R}{Z_1+Z_2+R}+\frac{Z_2 R}{Z_1+Z_2+R}}\\<br />&=&\frac{Z_1 Z_2}{Z_1+Z_2+R}+\frac{\left(\frac{\cancel{\left(Z_1+Z_2\right)}\left(R+Z_2\right)}{\cancel{Z_1+Z_2+R}}\right)\left(\frac{\left(Z_1+Z_2\right)\left(R+Z_1\right)}{Z_1+Z_2+R}\right)}{\frac{\cancel{\left(Z_1+Z_2\right)}\left(Z_1+Z_2+2R\right)}{\cancel{Z_1+Z_2+R}}}\\<br />&=&\frac{Z_1 Z_2}{Z_1+Z_2+R}+\frac{\left(Z_1+Z_2\right)\left(R+Z_2\right)\left(R+Z_1\right)}{\left(Z_1+Z_2+2R\right)\left(Z_1+Z_2+R\right)}\\<br />&=&\frac{Z_1 Z_2\left(Z_1+Z_2+2R\right)+\left(Z_1+Z_2\right)\left(R+Z_2\right)\left(R+Z_1\right)}{\left(Z_1+Z_2+2R\right)\left(Z_1+Z_2+R\right)}\\<br />&=&\frac{2 Z_1 Z_2\left(Z_1+Z_2\right)+R\left({Z_1}^2+2Z_1 Z_2+{Z_2}^2\right)+2R Z_1 Z_2+R^2\left(Z_1+Z_2\right)}{\left(Z_1+Z_2+2R\right)\left(Z_1+Z_2+R\right)}\\<br />&=&\frac{2 Z_1 Z_2\left(Z_1+Z_2\right)+R\left({Z_1}+{Z_2}\right)^2+R\left(2 Z_1 Z_2+R\left(Z_1+Z_2\right)\right)}{\left(Z_1+Z_2+2R\right)\left(Z_1+Z_2+R\right)}\\<br />&=&\frac{\left(Z_1+Z_2\right)\left(2 Z_1 Z_2+R\left({Z_1}+{Z_2}\right)\right)+R\left(2 Z_1 Z_2+R\left(Z_1+Z_2\right)\right)}{\left(Z_1+Z_2+2R\right)\left(Z_1+Z_2+R\right)}\\<br />&=&\frac{\cancel{\left(Z_1+Z_2+R\right)}\left(2 Z_1 Z_2+R\left(Z_1+Z_2\right)\right)}{\left(Z_1+Z_2+2R\right)\cancel{\left(Z_1+Z_2+R\right)}}\\<br />&=&\frac{2Z_1 Z_2+R\left(Z_1+Z_2\right)}{Z_1+Z_2+2R}\\<br />&=&\frac{2R^2+R\left(Z_1+Z_2\right)}{Z_1+Z_2+2R}\\<br />&=&\frac{R\cancel{\left(Z1+Z2+2R\right)}}{\cancel{Z_1+Z_2+2R}}\\<br />&=&R<br />Z_a&=&\frac{Z_1 Z_2}{Z_1+Z_2+R}\\<br />Z_b&=&\frac{Z_1 R}{Z_1+Z_2+R}\\<br />Z_c&=&\frac{Z_2 R}{Z_1+Z_2+R}\\<br />\end{eqnarray}$ ということで定抵抗回路となる。 Maxmaで処理すればfactor一発で答えが出るのだけれども、同じ結果を手計算で得ようとしたら予想外に式の操作が大変だった。更なる別解として等価電圧源と重ね合わせの理で導く方法も考えられるが、読者の課題としよう。

webadm	投稿日時: 2010-5-1 9:55
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【32】定抵抗回路長かった一端子対回路の演習問題も残すところあと２つ。最後は定抵抗回路に関する問題のみ。以下の回路が定抵抗回路になる条件を求めよというもの。以前に逆回路の問題で同様の回路を見ている。回路図内のRL直列回路とRC直列回路が互いにRに対して逆回路となれば定抵抗回路となる。従ってRL直列回路のインピーダンスをZ1、RC直列回路のインピーダンスをZ2とすると以下の条件が成り立てば良いことになる。 $Z_1 Z_2=R^2\,\forall\omega$ Z1,Z2はそれぞれ $\begin{eqnarray}<br />Z_1(j\omega)&=&j\omega L+R_1\\<br />Z_2(j\omega)&=&\frac{1}{j\omega C}+R_2<br />\end{eqnarray}$ 従って定抵抗回路となるためには $\begin{eqnarray}<br />Z_1(j\omega)Z_2(j\omega)&=&\left(j\omega L+R_1\right)\left(\frac{1}{j\omega C}+R_2\right)\\<br />&=&R_1 R_2+j\left(\omega L R2-\frac{R1}{\omega C}\right)+\frac{L}{C}\\<br />&=&R^2<br />\end{eqnarray}$ が周波数によらず常に満足すればいいのだが、周波数に依存してしまう、orz... だめだこりゃ(;´Д`) もともと回路がどうみても双対になってないし。逆回路を構成するのは無理ぽ。考え直そう。とりあえず駆動点インピーダンス関数は $\begin{eqnarray}<br />Z(s)&=&\frac{1}{\frac{1}{R}+\frac{1}{L s+R_1}}+\frac{1}{\frac{1}{R}+\frac{1}{\frac{1}{C s}+R_2}}\\<br />&=&\frac{R L\left(s+\frac{R_1}{L}\right)}{L\left(s+\frac{R_1+R}{L}\right)}+\frac{R C R_2\left(s+\frac{1}{C R_2}\right)}{C\left(R+R_2\right)\left(s+\frac{1}{C\left(R+R_2\right)}\right)}\\<br />&=&\frac{R \left(\cancel{L C}\left(R+R_2\right) \left(s+\frac{R_1}{L}\right)\left(s+\frac{1}{C\left(R+R_2\right)}\right)+R_2 \cancel{L C} \left(s+\frac{1}{C R_2}\right)\left(s+\frac{R_1+R}{L}\right)\right) }{\cancel{L C}\left(R+R_2\right) \left(s+\frac{R_1+R}{L}\right)\left(s+\frac{1}{C\left(R+R_2\right)}\right)}\\<br /><br />&=&\frac{R \left(\left(R+R_2\right) \left(s^2+\frac{R_1 C\left(R+R_2\right)+L}{L C\left(R+R_2\right)}s+\frac{R_1}{L C\left(R+R_2\right)}\right)+R_2 \left(s^2+\frac{L+C R_2\left(R_1+R\right)}{L C R_2}s+\frac{R_1+R}{L C R_2}\right)\right) }{\left(R+R_2\right) \left(s+\frac{R_1+R}{L}\right)\left(s+\frac{1}{C\left(R+R_2\right)}\right)}\\<br /><br />&=&\frac{R \left( \left(R+R_2\right)s^2+\frac{R_1 C\left(R+R_2\right)+L}{L C}s+\frac{R_1}{L C}+R_2 s^2+\frac{L+C R_2\left(R_1+R\right)}{L C }s+\frac{R_1+R}{L C}\right) }{\left(R+R_2\right) \left(s+\frac{R_1+R}{L}\right)\left(s+\frac{1}{C\left(R+R_2\right)}\right)}\\<br /><br />&=&\frac{R \left( \left(R+2R_2\right)s^2+\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L}{L C}s+\frac{R+2R_1}{L C}\right) }{\left(R+R_2\right) \left(s+\frac{R_1+R}{L}\right)\left(s+\frac{1}{C\left(R+R_2\right)}\right)}\\<br /><br />&=&\frac{R\left(R+2R_2\right) \left( s^2+\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L}{L C\left(R+2R_2\right)}s+\frac{R+2R_1}{L C\left(R+2R_2\right)}\right) }{\left(R+R_2\right) \left(s+\frac{R_1+R}{L}\right)\left(s+\frac{1}{C\left(R+R_2\right)}\right)}\\<br /><br />&=&\left(\frac{R\left(R+2R_2\right)}{\left(R+R_2\right)}\right)\frac{\left(s+\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L}{2L C\left(R+2R_2\right)}\right)^2-\left(\left(\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L}{2L C\left(R+2R_2\right)}\right)^2-\frac{R+2R_1}{L C\left(R+2R_2\right)}\right)}{ \left(s+\frac{R_1+R}{L}\right)\left(s+\frac{1}{C\left(R+R_2\right)}\right)}\\<br /><br />&=&\left(\frac{R\left(R+2R_2\right)}{\left(R+R_2\right)}\right)\frac{\left(s+\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L}{2L C\left(R+2R_2\right)}\right)^2-\left(\sqrt{\left(\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L}{2L C\left(R+2R_2\right)}\right)^2-\frac{R+2R_1}{L C\left(R+2R_2\right)}}\right)^2}{ \left(s+\frac{R_1+R}{L}\right)\left(s+\frac{1}{C\left(R+R_2\right)}\right)}\\<br /><br />&=&\left(\frac{R\left(R+2R_2\right)}{\left(R+R_2\right)}\right)\frac{\left(s+\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L}{2L C\left(R+2R_2\right)}-\sqrt{\left(\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L}{2L C\left(R+2R_2\right)}\right)^2-\frac{R+2R_1}{L C\left(R+2R_2\right)}}\right)\left(s+\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L}{2L C\left(R+2R_2\right)}+\sqrt{\left(\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L}{2L C\left(R+2R_2\right)}\right)^2-\frac{R+2R_1}{L C\left(R+2R_2\right)}}\right)}{ \left(s+\frac{R_1+R}{L}\right)\left(s+\frac{1}{C\left(R+R_2\right)}\right)}\\<br /><br />&=&\left(\frac{R\left(R+2R_2\right)}{\left(R+R_2\right)}\right)\frac{\left(s+\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L-\sqrt{\left(C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L\right)^2-4\left(R+2R_1\right)\left(L C\left(R+2R_2\right)\right)}}{2L C\left(R+2R_2\right)}\right)\left(s+\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L+\sqrt{\left(C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L\right)^2-4\left(R+2R_1\right)\left(L C\left(R+2R_2\right)\right)}}{2L C\left(R+2R_2\right)}\right)}{ \left(s+\frac{R_1+R}{L}\right)\left(s+\frac{1}{C\left(R+R_2\right)}\right)}\\<br /><br />&=&H\frac{\left(s+s_1\right)\left(s+s_3\right)}{ \left(s+s_2\right)\left(s+s_4\right)}\\<br /><br />&=&H\frac{s^2+\left(s_1+s_3\right)s+s_1 s_3}{ s^2+\left(s_2+s_4\right)s+s_2 s_4}\\<br /><br />H&=&\frac{R\left(R+2R_2\right)}{\left(R+R_2\right)}\\<br />s_1&=&\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L-\sqrt{\left(C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L\right)^2-4\left(R+2R_1\right)\left(L C\left(R+2R_2\right)\right)}}{2L C\left(R+2R_2\right)}\\<br />s_3&=&\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L+\sqrt{\left(C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L\right)^2-4\left(R+2R_1\right)\left(L C\left(R+2R_2\right)\right)}}{2L C\left(R+2R_2\right)}\\<br />s_2&=&\frac{R_1+R}{L}\\<br />s_4&=&\frac{1}{C\left(R+R_2\right)}<br /><br />\end{eqnarray}$ ということになり、s1,s3に零点をs2,s4に極を持つ。既に定抵抗回路の理論で学んだ通り、またLiouvilleの定理にあるようにすべてのsに対して正則で零点も極ももたない関数は唯一定数であるので、以下の様に零点s1,s3と極s2,s4が互いに相殺し合って消失しなければならないことになる。 $\begin{eqnarray}<br />Z(s)&=&H\frac{\left(s+s_1\right)\left(s+s_3\right)}{ \left(s+s_2\right)\left(s+s_4\right)}\\<br />&=&H\frac{s^2+\left(s_1+s_3\right)s+s_1 s_3}{ s^2+\left(s_2+s_4\right)s+s_2 s_4}\\<br />&=&H\,\,\forall s<br />\end{eqnarray}$ 上記の様に零点と極が互いに相殺し合う条件は、s1=s2かつs3=s4もしくはs1=s4かつs3=s2が成り立つ時で、その場合以下も成り立つことになる $\begin{eqnarray}<br />\frac{s_1+s_3}{s_2+s_4}&=&\frac{s_1 s_3}{s_2 s_4}=1<br />\end{eqnarray}$ s1,s2,s3,s4をそれぞれ代入してみると $\begin{eqnarray}<br />\frac{\left(R_2+R\right)\left(C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L\right)}{\left(2R_2+R\right)\left(C\left(R+R_1\right)\left(R+R_2\right)+L\right)}&=&\frac{\left( 2R1+R\right)\left( R2+R\right) }{\left( R1+R\right)\left( 2R2+R\right) }=1\\<br />\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L}{C\left(R+R_1\right)\left(R+R_2\right)+L}&=&\frac{\left( 2R1+R\right)}{\left( R1+R\right) }=\frac{\left(2R_2+R\right)}{\left(R_2+R\right)\\<br />\end{eqnarray}$ 従って少なくとも $R_1=R_2$ でなければならない。上記の関係を更に代入すると $\begin{eqnarray}<br />\frac{2C R_2\left(R+R_2\right)+2L}{C\left(R+R_2\right)^2+L}&=&\frac{\left(R+2R_2\right)}{\left(R+R_2\right) }\\<br /><br />\frac{2C R_2\left(R+R_2\right)^2+2L\left( R+R_2\right)}{C\left(R+R_2\right)^2\left(R+2R_2\right)+L\left(R+2R_2\right)}&=&1\\<br /><br />2C R_2\left(R+R_2\right)^2+2L\left( R+R_2\right)&=&C\left(R+R_2\right)^2\left(R+2R_2\right)+L\left(R+2R_2\right)\\<br /><br />L&=&C\left(R+R_2\right)^2\\<br /><br />\frac{L}{C}&=&\left(R+R_2\right)^2=\left(R+R_1\right)^2<br /><br />\end{eqnarray}$ という必要十分条件が導き出される。これも一種の不定方程式を解く問題である。これらのことから、回路網理論は数学の代数幾何学と表裏一体であることが判る。いずれ別の機会に代数幾何学を独学したいと思う。この分野に関しては戦後になって日本人数学者がめざましい貢献をしていたのだが工学における重要性が理解されるず、他の先進国に先取りされてしまった感がある。最先端のEDAツールや信号処理や検索エンジンではそれぞれ特有の不定方程式の解を有限時間で求めるためのアルゴリズム開発に数論的代数幾何学の知識が不可欠だからだ。

webadm	投稿日時: 2010-5-2 16:00
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	【33】続：定抵抗回路最後の問題。この問題は前問の別バリエーションとも言える。 LとCの直列回路のLとCにそれぞれ抵抗Rを並列接続して周波数によらずインピーダンスが一定となるようにするためのRの条件を示せというもの。この回路は前問でR1,R2を取り除いたもの、すなわちR1=R2=0と置いたものに等しい。前問と同様に駆動点インピーダンス関数の式をたてて解いても良いが、同じことなので、前問の解でR1=R2=0と置けば。 $\begin{eqnarray}<br />\frac{L}{C}&=&R^2\\<br />R&=&\sqrt{\frac{L}{C}}<br />\end{eqnarray}$ という結果が導き出される。これにて一端子対回路の演習問題を終了。長かったよﾏﾏﾝ(ﾉ∀`) 実に半年近く要したことになる。最初温いと思っていたのは大間違いだった。やはりというか、かなり数学の新しい分野とのリンクが多数潜んでいるので、大学の学部で一端子対回路が敬遠される理由がわかる。古い回路網理論の参考書とかでは、実に半分が数学の複素解析のおさらいにページを割いており、現在出版されている回路網理論の本では紹介されていないいくつもの理論や定理が説明されている。それらの理解には数論的代数幾何学の知識が不可欠である。そうした深淵な世界を一端覗いてしまうと代数幾何学にやおら興味が湧いてきた。既に参考書は入手してあるので、いずれ別掲示板で。

« 1 2 3 (4)

スレッド表示 | 新しいものから

前のトピック | 次のトピック | トップ

投稿するにはまず登録を

ページ変換(Google Translation)

EQPlayers
Allakhazam
EQresource VoA Home
Googleish(EN)
Googlean(KO)
Googlchinese(ZH-CN)
Googltwinese(ZH-TW)
Googlussian(RU)
Googlench(FR)
Googlerman(DE)
Googlabic(AR)
Googlindi(HI)
Googluguese(PT)
Googlutch(NL)
Googltarian(IT)
Googlpanish(ES)
Googlinnish(FJ)
Googlwedish(SY)
Googlatian(HR)
Googlzech(CS)
Googlgarian(BG)
Googlpolish(PL)
Googlmanian(RO)
Googlwegian(NO)
Googleek(EL)
Googldanish(DA)

サイト内検索

高度な検索