Gan's blog - フォーラム

« 1 (2) 3 4 »

投稿者	スレッド
webadm	投稿日時: 2010-4-24 11:55
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3094	【23】またまた：インピーダンス関数前問はインピーダンス関数をCauer展開だったが、今度はインピーダンス関数のFoster展開問題。以下の関数から２種類のFoster形回路を合成せよというもの。 $\text{(1)}\,Z_1(s)=\frac{\left(s+3\right)\left(s+5\right)}{\left(s+2\right)\left(s+4\right)}$ 第一Foster形だとインピーダンスの総和に展開されるので $\begin{eqnarray}<br />Z_1(s)&=&\frac{\left(s+3\right)\left(s+5\right)}{\left(s+2\right)\left(s+4\right)}\\<br />&=&\frac{H_1}{s+2}+\frac{H_2}{s+4}+H_\infty\\<br />&=&\frac{1}{C_1 s+G_1}+\frac{1}{C_2 s+G_2}+R_\infty\\<br />C_1&=&\frac{1}{H_1}=\frac{2}{3}\,[F]\\<br />G_1&=&\frac{2}{H_1}=\frac{4}{3}\,[S]\\<br />C_2&=&\frac{1}{H_2}=2\,[F]\\<br />G_2&=&\frac{4}{H_2}=8\,[S]\\<br />R_\infty&=&H_\infty=1\,[\Omega]\\<br />H_1&=&\lim_{s\to-2}\left(s+2\right)Z_1(s)\\<br />&=&\left.\frac{\left(s+3\right)\left(s+5\right)}{\left(s+4\right)}\right\|_{s=-2}\\<br />&=&\frac{\left(-2+3\right)\left(-2+5\right)}{\left(-2+4\right)}\\<br />&=&\frac{3}{2}\\<br />H_2&=&\lim_{s\to-4}\left(s+4\right)Z_1(s)\\<br />&=&\left.\frac{\left(s+3\right)\left(s+5\right)}{\left(s+2\right)}\right\|_{s=-4}\\<br />&=&\frac{\left(-4+3\right)\left(-4+5\right)}{\left(-4+2\right)}\\<br />&=&\frac{1}{2}\\<br />H_\infty&=&\lim_{s\to\infty}Z_1(s)\\<br />&=&\left.\frac{\left(s+3\right)\left(s+5\right)}{\left(s+2\right)\left(s+4\right)}\right\|_{s=\infty}\\<br />&=&\left.\frac{\left(1+\frac{3}{s}\right)\left(1+\frac{5}{s}\right)}{\left(1+\frac{2}{s}\right)\left(1+\frac{4}{s}\right)}\right\|_{s=\infty}\\<br />&=&1<br />\end{eqnarra}$ これは２つのRC並列回路と抵抗の直列接続となる。回路図に表すとということになる。もうひとつ第二Foster形は単純にアドミッタンスの総和へ部分分数展開すると負の留数が出てしまうのでちょっと操作する必要がある $\begin{eqnarray}<br />Y_1(s)&=&\frac{1}{Z_1(s)}\\<br />&=&\frac{\left(s+2\right)\left(s+4\right)}{\left(s+3\right)\left(s+5\right)}\\<br />&=&s\left(\frac{\left(s+2\right)\left(s+4\right)}{s\left(s+3\right)\left(s+5\right)}\right)\\<br />&=&s\left(\frac{H_0}{s}+\frac{H_1}{s+3}+\frac{H_2}{s+5}\right)\\<br />&=&H_0+\frac{H_1 s}{s+3}+\frac{H_2 s}{s+5}\\<br />&=&G_0+\frac{1}{R_1+\frac{1}{C_1 s}}+\frac{1}{R_2+\frac{1}{C_2 s}}\\<br />G_0&=&H_0=\frac{8}{15}\,[S]\\<br />R_1&=&\frac{1}{H_1}=6\,[\Omega]\\<br />C_1&=&\frac{H_1}{3}=\frac{1}{18}\,[F]\\<br />R_2&=&\frac{1}{H_2}=\frac{10}{3}\,[\Omega]\\<br />C_2&=&\frac{H_2}{5}=\frac{3}{50}\,[F]\\<br />H_0&=&\lim_{s\to0}Y_1(s)\\<br />&=&\left.\frac{\left(s+2\right)\left(s+4\right)}{\left(s+3\right)\left(s+5\right)}\right\|_{s=0}\\<br />&=&\frac{\left(0+2\right)\left(0+4\right)}{\left(0+3\right)\left(0+5\right)}\\<br />&=&\frac{8}{15}\\<br />H_1&=&\lim_{s\to-3}\frac{\left(s+3\right)Y_1(s)}{s}\\<br />&=&\left.\frac{\left(s+2\right)\left(s+4\right)}{s\left(s+5\right)}\right\|_{s=-3}\\<br />&=&\frac{\left(-3+2\right)\left(-3+4\right)}{-3\left(-3+5\right)}\\<br />&=&\frac{1}{6}\\<br />H_2&=&\lim_{s\to-5}\frac{\left(s+5\right)Y_1(s)}{s}\\<br />&=&\left.\frac{\left(s+2\right)\left(s+4\right)}{s\left(s+3\right)}\right\|_{s=-4}\\<br />&=&\frac{\left(-5+2\right)\left(-5+4\right)}{-5\left(-5+3\right)}\\<br />&=&\frac{3}{10}<br />\end{eqnarra}$ 従って２つのRC直列回路と抵抗の並列接続で構成される。回路図に描くとということになる。 $\text{(2)}\,Z_2(s)=\frac{s\left(s+3\right)\left(s+5\right)}{\left(s+2\right)\left(s+4\right)}$ 前の設問の式の分子の次数がひとつ多くなっただけだが、単純に部分分数展開すると負の留数が出てしまうのでちょっとした数式操作が必要だ。 $\begin{eqnarray}<br />Z_2(s)&=&\frac{s\left(s+3\right)\left(s+5\right)}{\left(s+2\right)\left(s+4\right)}\\<br />&=&s\left(\frac{\left(s+3\right)\left(s+5\right)}{\left(s+2\right)\left(s+4\right)}\right)\\<br />&=&s\left(\frac{H_1}{s+2}+\frac{H_2}{s+4}+H_\infty\right)\\<br />&=&\frac{H_1 s}{s+2}+\frac{H_2 s}{s+4}+H_\infty s\\<br />&=&\frac{1}{G_1+\frac{1}{L_1 s}}+\frac{1}{G_2+\frac{1}{L_2 s}}+L_\infty s\\<br />G_1&=&\frac{1}{H_1}=\frac{2}{3}\,[S]\\<br />L_1&=&\frac{H_1}{2}=\frac{3}{4}\,[H]\\<br />G_2&=&\frac{1}{H_2}=2\,[S]\\<br />L_2&=&\frac{H_2}{4}=\frac{1}{8}\,[H]\\<br />L_\infty&=&H_\infty=1\,[H]\\<br />H_1&=&\lim_{s\to-2}\frac{\left(s+2\right)Z_2(s)}{s}\\<br />&=&\left.\frac{\left(s+3\right)\left(s+5\right)}{\left(s+4\right)}\right\|_{s=-2}\\<br />&=&\frac{\left(-2+3\right)\left(-2+5\right)}{\left(-2+4\right)}\\<br />&=&\frac{3}{2}\\<br />H_2&=&\lim_{s\to-4}\frac{\left(s+4\right)Z_2(s)}{s}\\<br />&=&\left.\frac{\left(s+3\right)\left(s+5\right)}{\left(s+2\right)}\right\|_{s=-4}\\<br />&=&\frac{\left(-4+3\right)\left(-4+5\right)}{\left(-4+2\right)}\\<br />&=&\frac{1}{2}\\<br />H_\infty&=&\lim_{s\to\infty}\frac{Z_2(s)}{s}\\<br />&=&\left.\frac{\left(s+3\right)\left(s+5\right)}{\left(s+2\right)\left(s+4\right)}\right\|_{s=\infty}\\<br />&=&\left.\frac{\left(1+\frac{3}{s}\right)\left(1+\frac{5}{s}\right)}{\left(1+\frac{2}{s}\right)\left(1+\frac{4}{s}\right)}\right\|_{s=\infty}\\<br />&=&1<br />\end{eqnarray}$ 従って２つのRL並列回路と抵抗の直列接続となる。回路図に描くとということになる。第二Foster展開は逆に単純にアドミッタンスの総和へ部分分数展開すればよく $\begin{eqnarray}<br />Y_2(s)&=&\frac{1}{Z_2(s)}\\<br />&=&\frac{\left(s+2\right)\left(s+4\right)}{s\left(s+3\right)\left(s+5\right)}\\<br />&=&\frac{H_0}{s}+\frac{H_1}{s+3}+\frac{H_2}{s+5}\\<br />&=&\frac{1}{L_0 s}+\frac{1}{L_1 s+R_1}+\frac{1}{L_2 s+R_2}\\<br />L_0&=&\frac{1}{H_0}=\frac{15}{8}\,[H]\\<br />L_1&=&\frac{1}{H_1}=6\,[H]\\<br />R_1&=&\frac{3}{H_1}=18\,[\Omega]\\<br />L_2&=&\frac{1}{H_2}=\frac{10}{3}\,[H]\\<br />R_2&=&\frac{5}{H_2}=\frac{50}{3}\,[\Omega]\\<br />H_0&=&\lim_{s\to0}sY_2(s)\\<br />&=&\left.\frac{\left(s+2\right)\left(s+4\right)}{\left(s+3\right)\left(s+5\right)}\right\|_{s=0}\\<br />&=&\frac{\left(0+2\right)\left(0+4\right)}{\left(0+3\right)\left(0+5\right)}\\<br />&=&\frac{8}{15}\\<br />H_1&=&\lim_{s\to-3}\left(s+3\right)Y_2(s)\\<br />&=&\left.\frac{\left(s+2\right)\left(s+4\right)}{s\left(s+5\right)}\right\|_{s=-3}<br />&=&\frac{\left(-3+2\right)\left(-3+4\right)}{-3\left(-3+5\right)}\\<br />&=&\frac{1}{6}\\<br />H_2&=&\lim_{s\to-5}\left(s+5\right)Y_2(s)\\<br />&=&\left.\frac{\left(s+2\right)\left(s+4\right)}{s\left(s+3\right)}\right\|_{s=-5}\\<br />&=&\frac{\left(-5+2\right)\left(-5+4\right)}{-5\left(-5+3\right)}\\<br />&=&\frac{3}{10}<br />\end{eqnarray}$ ということで２つのRL直列回路とLとの並列接続で構成される。回路図に描くとということになる。

webadm	投稿日時: 2010-4-24 4:03
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3094	【22】続々：インピーダンス関数次ぎもインピーダンス関数の問題で、以下に示された関数をCauer展開し二種類の受動素子だけで実現できるか確かめ、実現できるものについては回路を示せというもの。 $\text{(1)}\,Z_a(s)=\frac{15s^4+166s^2+144}{10s^3+84s}$ 分子の次数が分母よりも大きいので次数の大きな項から切り出していくことにする。 $\begin{eqnarray}<br />Z_a(s)&=&\frac{15s^4+166s^2+144}{10s^3+84s}\\<br />&=&\frac{15}{10}s+\frac{\left(166-\frac{15\cdot 84}{10}\right)s^2+144}{10s^3+84s}\\<br />&=&\frac{3}{2}s+\frac{1}{\Large\frac{10s^3+84s}{40s^2+144}}\\<br />&=&\frac{3}{2}s+\frac{1}{\Large\frac{10}{40}s+\frac{\left(84-\frac{10\cdot 144}{40}\right)s}{40s^2+144}}\\<br />&=&\frac{3}{2}s+\frac{1}{\Large\frac{1}{4}s+\frac{48s}{40s^2+144}}\\<br />&=&\frac{3}{2}s+\frac{1}{\Large\frac{1}{4}s+\frac{1}{\frac{5}{6}s+\frac{144}{48s}}}\\<br />&=&\frac{3}{2}s+\frac{1}{\Large\frac{1}{4}s+\frac{1}{\frac{5}{6}s+\frac{3}{s}}}\\<br />&=&L_1 s+\frac{1}{\Large C_2 s+\frac{1}{L_3 s+\frac{1}{C_4 s}}}\\<br />L_1&=&\frac{3}{2}\,[H]\\<br />C_2&=&\frac{1}{4}\,[F]\\<br />L_3&=&\frac{5}{6}\,[H]\\<br />C_4&=&\frac{1}{3}\,[F]<br />\end{eqnarray}$ 従ってLとCの二種類の受動素子のラダー回路で実現できる。回路図を描くとということになる。 $\text{(2)}\,Z_b(s)=\frac{18s^3+6s^2+6s+1}{6s^2+2s+1}$ 次ぎも同様に次数の大きな項から切り出していくと $\begin{eqnarray}<br />Z_b(s)&=&\frac{18s^3+6s^2+6s+1}{6s^2+2s+1}\\<br />&=&\frac{18}{6}s+\frac{\left(6-\frac{18\cdot 2}{6}\right)s^2+\left(6-\frac{18}{6}\right)s+1}{6s^2+2s+1}\\<br />&=&3s+\frac{3s+1}{6s^2+2s+1}\\<br />&=&3s+\frac{1}{\Large\frac{6s^2+2s+1}{3s+1}}\\<br />&=&3s+\frac{1}{\Large 2s+\frac{1}{3s+1}}\\<br />&=&L_1 s+\frac{1}{\Large C_2 s+\frac{1}{L_3 s+R_4}}\\<br />L_1&=&3\,[H]\\<br />C_2&=&2\,[F]\\<br />L_3&=&3\,[H]\\<br />R_4&=&1\,[\Omega]<br />\end{eqnarray}$ 従ってLCRラダー回路となるため二種類の素子だけでは実現できない。 $\text{(3)}\,Z_c(s)=\frac{36s^4+4s^2-1}{18s^3-s}$ これはリアクタンス関数ぽいが負の定数項がある時点でアウトだろうと思う。一応次数の高い項から切り出すと $\begin{eqnarray}<br />Z_c(s)&=&\frac{36s^4+4s^2-1}{18s^3-s}\\<br />&=&\frac{36}{18}s+\frac{\left(4+\frac{36}{18}\right)s^2-1}{18s^3-s}\\<br />&=&2s+\frac{1}{\Large\frac{18}{6}s+\frac{\left(\frac{18}{6}-1\right)s}{6s^2-1}}\\<br />&=&2s+\frac{1}{\Large\frac{18}{6}s+\frac{2s}{6s^2-1}}\\<br />&=&2s+\frac{1}{\Large 3s+\frac{1}{3s-\frac{1}{2s}}}\\<br />&=&L_1 s+\frac{1}{\Large C_2 s+\frac{1}{L_3 s+\frac{1}{C_4 s}}}\\<br />L_1&=&2\,[H]\\<br />C_2&=&3\,[F]\\<br />L_3&=&3\,[H]\\<br />C_4&=&-2\,[F]<br />\end{eqnarray}$ 最後の素子が負のキャパシタンスを持つことから２種類の受動素子では実現できない。 $\text{(4)}\,Z_d(s)=\frac{576s^3+388s^2+55s+1}{288s^2+122s+9}$ 最後のはまともそうだ。次数の高い項から切り出すと $\begin{eqnarray}<br />Z_d(s)&=&\frac{576s^3+388s^2+55s+1}{288s^2+122s+9}\\<br />&=&\frac{576}{288}s+\frac{\left(388-\frac{576\cdot 122}{288}\right)s^2+\left(55-\frac{576\cdot 9}{288}\right)s+1}{288s^2+122s+9}\\<br />&=&2s+\frac{\144s^2+37s+1}{288s^2+122s+9}\\<br />&=&2s+\frac{1}{\Large 2+\frac{\left(122-2\cdot 37\right)s+\left(9-2\right)}{\144s^2+37s+1}}\\<br />&=&2s+\frac{1}{\Large 2+\frac{1}{\frac{\144s^2+37s+1}{48s+7}}}\\<br />&=&2s+\frac{1}{\Large 2+\frac{1}{\frac{144}{48}s+\frac{\left(37-\frac{144\cdot 7}{48}\right)s+1}{48s+7}}}\\<br />&=&2s+\frac{1}{\Large 2+\frac{1}{3s+\frac{1}{\frac{48s+7}{16s+1}}}}\\<br />&=&2s+\frac{1}{\Large 2+\frac{1}{3s+\frac{1}{3+\frac{4}{16s+1}}}}\\<br />&=&L_1 s+\frac{1}{\Large G_2+\frac{1}{L_3 s+\frac{1}{G_4+\frac{4}{L_5 s+R_6}}}}\\<br />L_1&=&2\,[H]\\<br />G_2&=&2\,[S]\\<br />L_3&=&3\,[H]\\<br />G_4&=&3\,[S]\\<br />L_5&=&2\,[H]\\<br />R_6&=&\frac{1}{4}\,[\Omega]<br />\end{eqnarray}$ 従ってRLラダー回路で構成できる。回路図で表すとということになる。

webadm	投稿日時: 2010-4-22 12:29
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3094	【21】続：インピーダンス関数しばらくインピーダンス関数に関わる問題が続く。与えられた関数がインピーダンスとして実現できるか否かを判定し、実現できるものについては二種類の受動素子だけで実現できるかどうかを調べよというもの。 $\text{(1)}\,\frac{s\left(s^2+5\right)\left(s^2+6\right)}{\left(s^2+3\right)\left(s^2+4\right)}$ これは零点と極がいずれも一位で虚軸上に存在するため正実関数の必要条件を満たすものの、リアクタンス関数の必要条件である零点と極が交互に並ぶ条件を満たしていない。実際に部分分数展開してみるとはっきりする。 $\begin{eqnarray}<br />Z(s)&=&\frac{s\left(s^2+5\right)\left(s^2+6\right)}{\left(s^2+3\right)\left(s^2+4\right)}\\<br />&=&-\frac{2\,s}{{s}^{2}+4}+\frac{6\,s}{{s}^{2}+3}+s<br />\end{eqnarray}$ 負の留数を持つので正実関数の必要条件を満たしておらず２種類の受動素子では実現できない。 $\text{(2)}\,\frac{\left(s+5\right)}{\left(s+3\right)\left(s+4\right)}$ これは零点と極がいずれも実軸上で左半面にあり正実関数の必要条件を満たしているが、零点と極が交互に並んでないため十分ではない。これも部分分数に展開してみると $\begin{eqnarray}<br />Z(s)&=&\frac{\left(s+5\right)}{\left(s+3\right)\left(s+4\right)}\\<br />&=&\frac{2}{s+3}-\frac{1}{s+4}<br />\end{eqnarray}$ 負の留数を伴うため二種類の受動素子だけでは実現できない。 $\text{(3)}\,\frac{\left(s+1\right)\left(s+3\right)}{\left(s+2\right)}$ これは零点と極が実軸上にあり、交互に現れることからよさそうである。部分分数展開してみると $\begin{eqnarray}<br />Z(s)&=&\frac{\left(s+1\right)\left(s+3\right)}{\left(s+2\right)}\\<br />&=&\frac{1}{\frac{\left(s+2\right)}{\left(s+1\right)\left(s+3\right)}}\\<br />&=&\frac{1}{\frac{1}{2\,\left( s+3\right) }+\frac{1}{2\,\left( s+1\right) }}\\<br />&=&\frac{1}{\frac{1}{L_1 s+R_1}+\frac{1}{L_2 s+R_2}}\\<br />L_1&=&2\,[H]\\<br />R_1&=&6\,[\Omega]\\<br />L_2&=&2\,[H]\\<br />R_2&=&2\,[\Omega]<br />\end{eqnarray}$ 従って２つのLR直列回路が並列に接続された回路で実現できることになる。 $\text{(4)}\,\frac{s^3+6s}{\left(s^2+5\right)\left(s^2+7\right)}$ 分子の多項式が因数分解されていないが、零点と極がいずれも一位で虚軸上にのみ現れるので正実関数かつリアクタンス関数である。部分分数展開すると $\begin{eqnarray}<br />Z(s)&=&\frac{s^3+6s}{\left(s^2+5\right)\left(s^2+7\right)}\\<br />&=&\frac{s\left(s^2+6\right)}{\left(s^2+5\right)\left(s^2+7\right)}\\<br />&=&\frac{s}{2\,\left( {s}^{2}+7\right) }+\frac{s}{2\,\left( {s}^{2}+5\right) }\\<br />&=&\frac{1}{C_1 s+\frac{1}{L_1 s}}+\frac{1}{C_2 s+\frac{1}{L_2 s}}\\<br />C_1&=&2\,[F]\\<br />L_1&=&\frac{1}{14}\,[H]\\<br />C_2&=&2\,[F]\\<br />L_2&=&\frac{1}{10}\,[H]<br />\end{eqnarray}$ 従って２つのLC並列回路の直列接続で実現できる。ここだけの話だが分子の式を最初書き写し間違えてs^3がs^2になっていて次数が一つ足らず零点が実軸上に現れてしまう変な式になってしまって焦ったのは内緒だ。 $\text{(5)}\,\frac{s^2+2}{\left(s+2\right)\left(s+3\right)}$ これは零点が虚軸上に極が実軸上にあるので正実関数のように見えるがs=jωとして正実関数であるためには $\begin{eqnarray}<br />Re\left(Z(j\omega)\right)&=&Re\left(\frac{-{\omega}^2+2}{\left(j\omega+2\right)\left(j\omega+3\right)}\right)\\<br />&=&Re\left(\frac{2-{\omega}^2}{6-{\omega}^2+j5\omega}\right)\\<br />&=&Re\left(\frac{\left(2-{\omega}^2\right)\left(6-{\omega}^2-j5\omega\right)}{\left(6-{\omega}^2\right)^2+\left(5\omega\right)^2}\right)\\<br />&=&\frac{\left(2-{\omega}^2\right)\left(6-{\omega}^2\right)}{\left(6-{\omega}^2\right)^2+\left(5\omega\right)^2}\ge0\,\forall\omega<br />\end{eqnarray}$ を満足しなければならないが、 2＜ω^2＜6 の範囲では条件を満たさないので正実関数ではないということになる。 $\text{(6)}\,\frac{\left(s+4\right)\left(s+7\right)}{\left(s+3\right)\left(s+6\right)}$ これは零点と極が一位で実軸上かつ左半面にのみ存在し、零点と極が交互に位置しているのでよさそうである。s=jωと置いて実数部を確かめてみると $\begin{eqnarray}<br />Re\left(Z(j\omega)\right)&=&Re\left(\frac{\left(j\omega+4\right)\left(j\omega+7\right)}{\left(j\omega+3\right)\left(j\omega+6\right)}\right)\\<br />&=&Re\left(\frac{28-{\omega}^2+j11\omega}{18-{\omega}^2+j9\omega}\right)\\<br />&=&Re\left(\left(\frac{28-{\omega}^2+j11\omega\right)\left(18-{\omega}^2-j9\omega\right)}{\left(18-{\omega}^2\right)^2+\left(9\omega\right)^2}\right)\\<br />&=&\frac{\left(28-{\omega}^2\right)\left(18-{\omega}^2\right)+99\omega^2}{\left(18-{\omega}^2\right)^2+\left(9\omega\right)^2}\\<br />&=&\frac{{\omega}^4+53\omega^2+504}{\left(18-{\omega}^2\right)^2+\left(9\omega\right)^2}\ge0\,\forall\omega<br />\end{eqnarray}$ が成り立つので正実関数である。部分分数に展開すると $\begin{eqnarray}<br />Z(s)&=&\frac{\left(s+4\right)\left(s+7\right)}{\left(s+3\right)\left(s+6\right)}\\<br />&=&\frac{H_1}{s+3}+\frac{H_2}{s+6}+H_\infty\\<br />&=&\frac{1}{C_1 s+G_1}+\frac{1}{C_2 s+G_2}+R_\infty\\<br />C_1&=&\frac{1}{H_1}=\frac{3}{4}\,[F]\\<br />G_1&=&\frac{3}{H_1}=\frac{9}{4}\,[S]\\<br />C_2&=&\frac{1}{H_2}=\frac{3}{2}\,[F]\\<br />G_2&=&\frac{6}{H_2}=\frac{18}{2}\,[S]\\<br />R_\infty&=&H_\infty=1\,[\Omega]\\<br />H_1&=&\lim_{s\to-3}\left(s+3\right)Z(s)\\<br />&=&\left.\frac{\left(s+4\right)\left(s+7\right)}{\left(s+6\right)}\right\|_{s=-3}\\<br />&=&\frac{\left(-3+4\right)\left(-3+7\right)}{\left(-3+6\right)}\\<br />&=&\frac{4}{3}\\<br />H_2&=&\lim_{s\to-6}\left(s+6\right)Z(s)\\<br />&=&\left.\frac{\left(s+4\right)\left(s+7\right)}{\left(s+3\right))}\right\|_{s=-6}\\<br />&=&\frac{\left(-6+4\right)\left(-6+7\right)}{\left(-6+3\right))}\\<br />&=&\frac{2}{3}\\<br />H_\infty&=&\lim_{s\to\infty}Z(s)\\<br />&=&\left.\frac{\left(s+4\right)\left(s+7\right)}{\left(s+3\right)\left(s+6\right)}\right\|_{s=\infty}\\<br />&=&\left.\frac{\left(1+\frac{4}{s}\right)\left(1+\frac{7}{s}\right)}{\left(1+\frac{3}{s}\right)\left(1+\frac{6}{s}\right)}\right\|_{s=\infty}\\<br />&=&1<br />\end{eqnarray}$ ということで２つのRC並列回路とひとつの抵抗の直列接続で実現できる。 $\text{(7)}\,\frac{2}{s+3}+2-\frac{2}{s+4}$ これは一見すると有理関数の形をしていないのと分子の係数に負の値があるので正実関数でないように見えるが、s=jωとして実数部を調べてみると $\begin{eqnarray}<br />Re\left(Z(j\omega)\right)&=&Re\left(\frac{2}{j\omega+3}+2-\frac{2}{j\omega+4}\right)\\<br />&=&Re\left(\frac{2\left(j\omega+4\right)+2\left(j\omega+3\right)\left(j\omega+4\right)-2\left(j\omega+3\right)}{\left(j\omega+3\right)\left(j\omega+4\right)}\right)\\<br />&=&Re\left(\frac{\cancel{j2\omega}+8+2\left(12-{\omega}^2+j7\omega\right)-\cancel{j2\omega}-6}{12-{\omega}^2+j7\omega}\right)\\<br />&=&Re\left(\frac{\left(26-2{\omega}^2+j14\omega\right)\left(12-{\omega}^2-j7\omega\right)}{\left(12-{\omega}^2\right)^2+\left(7\omega\right)^2}\right)\\<br />&=&\frac{\left(26-2{\omega}^2\right)\left(12-{\omega}^2\right)+98\omega^2}{\left(12-{\omega}^2\right)^2+\left(7\omega\right)^2}\\<br />&=&\frac{2{\omega}^4+48\omega^2+312}{\left(12-{\omega}^2\right)^2+\left(7\omega\right)^2}\ge0\,\forall\omega<br />\end{eqnarray}$ が成立するので正実関数である。部分分数展開すると $\begin{eqnarray}<br />Z(s)&=&\frac{2}{s+3}+2-\frac{2}{s+4}\\<br />&=&\frac{2}{s+3}+\frac{2s+6}{s+4}\\<br />&=&\frac{2}{s+3}+\frac{2s}{s+4}+\frac{6}{s+4}\\<br />&=&\frac{1}{C_1 s+G_1}+\frac{1}{G_2+\frac{1}{L_2 s}}+\frac{1}{C_3 s+G_3}\\<br />C_1&=&\frac{1}{2}\,[F]\\<br />G_1&=&\frac{3}{2}\,[S]\\<br />G_2&=&\frac{1}{2}\,[S]\\<br />L_2&=&\frac{1}{2}\,[H]\\<br />C_3&=&\frac{1}{6}\,[F]\\<br />G_3&=&\frac{2}{3}\,[S]<br />\end{eqnarray}$ ということで２つのRC並列回路とひとつのRL並列回路の直列接続が必要となり、２種類の素子だけでは実現できないということになる。 $\text{(8)}\,\frac{s^3+9s^2+23s+15}{s^2+6s+8}$ これはなんだか判らないけど、s=jωとして実数部を調べてみると $\begin{eqnarray}<br />Re\left(Z(j\omega)\right)&=&Re\left(\frac{-j{\omega}^3-9{\omega}^2+j23\omega+15}{-{\omega}^2+j6\omega+8}\right)\\<br />&=&Re\left(\frac{\left(15-9{\omega}^2+j\omega\left(23-{\omega}^2\right)\right)\left(8-{\omega}^2-j6\omega\right)}{\left(8-{\omega}^2\right)^2+\left(6\omega\right)^2}\right)\\<br />&=&\frac{\left(15-9{\omega}^2\right)\left(8-{\omega}^2\right)+6{\omega}^2\left(23-{\omega}^2\right)}{\left(8-{\omega}^2\right)^2+\left(6\omega\right)^2}\\<br />&=&\frac{9{\omega}^4-87{\omega}^2+120+138{\omega}^2-6{\omega}^4}{\left(8-{\omega}^2\right)^2+\left(6\omega\right)^2}\\<br />&=&\frac{3{\omega}^4+51{\omega}^2+120}{\left(8-{\omega}^2\right)^2+\left(6\omega\right)^2}\ge0\,\forall\omega<br />\end{eqnarray}$ が成り立つので正実関数である。部分分数展開してみると $\begin{eqnarray}<br />Z(s)&=&\frac{s^3+9s^2+23s+15}{s^2+6s+8}\\<br />&=&\frac{\left(s+1\right)\left(s+3\right)\left(s+5\right)}{\left(s+2\right)\left(s+4\right)}\\<br />&=&\frac{1}{\frac{\left(s+2\right)\left(s+4\right)}{\left(s+1\right)\left(s+3\right)\left(s+5\right)}}\\<br />&=&\frac{1}{\frac{H_1}{s+1}+\frac{H_2}{s+3}+\frac{H_3}{s+5}}\\<br />&=&\frac{1}{\frac{1}{L_1 s+R_1}+\frac{1}{L_2 s+R_2}+\frac{1}{L_3 s+R_3}}\\<br />L_1&=&\frac{1}{H_1}=\frac{8}{3}\,[H]\\<br />R_1&=&\frac{1}{H_1}=\frac{3}{8}\,[\Omega]\\<br />L_2&=&\frac{1}{H_2}=4\,[H]\\<br />R_2&=&\frac{3}{H_2}=12\,[\Omega]\\<br />L_3&=&\frac{1}{H_3}=\frac{8}{3}\,[H]\\<br />R_3&=&\frac{5}{H_3}=\frac{40}{3}\,[\Omega]\\<br />H_1&=&\lim_{s\to-1}\left(s+1\right)Y(s)\\<br />&=&\left.\frac{\left(s+2\right)\left(s+4\right)}{\left(s+3\right)\left(s+5\right)}\right\|_{s=-1}\\<br />&=&\frac{\left(-1+2\right)\left(-1+4\right)}{\left(-1+3\right)\left(-1+5\right)}\\<br />&=&\frac{3}{8}\\<br />H_2&=&\lim_{s\to-3}\left(s+3\right)Y(s)\\<br />&=&\left.\frac{\left(s+2\right)\left(s+4\right)}{\left(s+1\right)\left(s+5\right)}\right\|_{s=-3}\\<br />&=&\frac{\left(-3+2\right)\left(-3+4\right)}{\left(-3+1\right)\left(-3+5\right)}\\<br />&=&\frac{1}{4}\\<br />H_3&=&\lim_{s\to-5}\left(s+5\right)Y(s)\\<br />&=&\left.\frac{\left(s+2\right)\left(s+4\right)}{\left(s+1\right)\left(s+3\right)}\right\|_{s=-5}\\<br />&=&\frac{\left(-5+2\right)\left(-5+4\right)}{\left(-5+1\right)\left(-5+3\right)}\\<br />&=&\frac{3}{8}<br />\end{eqnarray}$ ということで３つのRL直列回路の並列接続で実現できるため２種類の素子で実現可能。 $\text{(9)}\,\frac{s^2+10}{\left(s+5\right)\left(s+2\right)}$ 最後のは零点が複素共役対で極が実軸上でそれぞれ左半面にあるがどうだろう。s=jωとして実数部を調べてみると $\begin{eqnarray}<br />Re\left(Z(j\omega)\right)&=&Re\left(\frac{-{\omega}^2+10}{\left(j\omega+5\right)\left(j\omega+2\right)}\right)\\<br />&=&Re\left(\frac{10-{\omega}^2}{10-{\omega}^2+j7\omega}\right)\\<br />&=&Re\left(\frac{\left(10-{\omega}^2\right)\left(10-{\omega}^2-j7\omega\right)}{\left(10-{\omega}^2\right)^2+\left(7\omega\right)^2}\right)\\<br />&=&\frac{\left(10-{\omega}^2\right)^2}{\left(10-{\omega}^2\right)^2+\left(7\omega\right)^2}\ge0\,\forall\omega<br />\end{eqnarray}$ が成り立つので正実関数ではあるが、零点と極が交互に現れないので受動素子だけでは実現できない。部分分数展開してみても $\begin{eqnarray}<br />Z(s)&=&\frac{s^2+10}{\left(s+5\right)\left(s+2\right)}\\<br />&=&\frac{H_1}{s+5}+\frac{H_2}{s+2}+H_\infty\\<br />H_1&=&\lim_{s\to-5}\left(s+5\right)Z(s)\\<br />&=&\left.\frac{s^2+10}{\left(s+2\right)}\right\|_{s=-5}<br />&=&\frac{5^+10}{\left(-5+2\right)}\\<br />&=&-\frac{35}{3}\\<br />H_2&=&\lim_{s\to-2}\left(s+2\right)Z(s)\\<br />&=&\left.\frac{s^2+10}{\left(s+5\right)}\right\|_{s=-2}<br />&=&\frac{2^2+10}{\left(-2+5\right)}\\<br />&=&-\frac{14}{3}\\<br />H_\infty&=&\lim_{s\to\infty}Z(s)\\<br />&=&\left.\frac{s^2+10}{\left(s+5\right)\left(s+2\right)}\right\|_{s=\infty}\\<br />&=&\left.\frac{1+\frac{10}{s^2}}{\left(1+\frac{5}{s}\right)\left(1+\frac{2}{s}\right)}\right\|_{s=\infty}\\<br />&=&1<br />\end{eqnarray}$ という具合に負の留数を持つため受動素子だけでは実現できないことになる。こうしてみると複素共役対の特異点を持つ関数も正実関数であるものの、負の留数を持つため受動素子だけでは実現できないが、負のインダクタンスやキャパシタンス、負の抵抗は真空管やトランジスタのような能動素子を使用すれば実現できる。特に複素平面上の楕円曲線上に複素共役対として複数の特異点を持つ楕円有理関数はフィルターとして良好な周波数特性を備える。後々これら楕円関数フィルターに関して学ぶにも基礎となる二端子回路の理論を知っておく必要がある。

webadm	投稿日時: 2010-4-21 23:11
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3094	【20】インピーダンス関数終わったと思っていた正実関数の問題が再び出てきた。以下の関数が正実関数となる正の実数なる係数、a,b,cの間の関係条件を示せというもの。加えてRL回路またはRC回路のインピーダンス関数として実現されるにはa,b,cにどのような条件が必要が示せというもの。 $Z(s)=\frac{s+c}{\left(s+a\right)\left(s+b\right)}$ s=jωと置くとインピーダンス関数の実数部は $\begin{eqnarray}<br />Re\left(Z(j\omega)\right)&=&\frac{j\omega+c}{\left(j\omega+a\right)\left(j\omega+b\right)}\\<br />&=&Re\left(\frac{j\omega+c}{ab-{\omega}^2+j\left(a+b\right)\omega}\right)\\<br />&=&Re\left(\frac{\left(j\omega+c\right)\left(\left(ab-{\omega}^2\right)-j\left(a+b\right)\omega\right)}{\left(\left(ab-{\omega}^2\right)^2+\left(a+b\right)^2\omega^2\right)}\right)\\<br />&=&\frac{\left(a+b\right)\omega^2+c\left(ab-{\omega}^2\right)}{{\omega}^4-\cancel{2ab{\omega}^2}+a^2b^2+\left(a^2+\cancel{2ab}+b^2\right)\omega^2}\\<br />&=&\frac{\left(a+b-c\right)\omega^2+abc}{\left(s^2+a^2\right)\left(s^2+b^2\right)}\ge 0\,\forall\omega<br />\end{eqnarray}$ ということになる。すなわち正実関数であるための必要十分条件は $\begin{eqnarray}<br />a+b-c\ge0\\<br />a+b\ge c<br />\end{eqnarray}$ ということになる。 RL回路、RC回路はLC回路と同様に零点と極が交互に現れる必要から問題の関数では実軸上に-a,-bの２つの極と-cに零点を持つことから a＜c＜b もしくは b＜c＜a ということになる。著者の解答ではa≦c≦bもしくはb≦c≦aとあるが、a,b,cが互いに等しいものがあると零点と極が消滅してしまうので元のインピーダンス関数とは違ってしまう。

webadm	投稿日時: 2010-4-20 9:55
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3094	【19】またまた：リアクタンス回路これでリアクタンス回路の問題は最後。以下の回路図で示されているリアクタンス回路と等価な回路をそれぞれ３つずつ示せというもの。与えられているのは第一Foster展開形のリアクタンス回路。したがって第二Foster展開形と第一と第二のCauer展開形の３つに展開し直せば良いことになる。回路から関数式を起こして展開し直してもよいが、回路素子の定数は問われていないのでその必要はない。第一Foster展開形と第二Foster展開形は互いに双対回路なので、並列と直列、インダクタンスとキャパシタンスが一対一で対応するのでそれでもよい。また第一Foster展開形と第二Foster我々は既に理論でFoster展開に関してω=0,∞が零点か極かの組み合わせによって回路の形が決まることを学んでいる。引用：これらのことから、Foster第一形式は以下の４ケースに分類される。 $\begin{array}<br />Case & \omega=0 & \omega=\infty & C_0 & L_\infty\\<br /> 1 & pole & pole & present & present\\<br /> 2 & zero & zero & short-circuited & short-circuited\\<br /> 3 & pole & zero & preset & short-circuited\\<br /> 4 & zero & pole & short-circuited & presetnt<br />\end{array}$ 同様のことがFoster第二形式についてもあてはまる。 $\begin{array}<br />Case & \omega=0 & \omega=\infty & L_0 & C_\infty\\<br /> 1 & pole & pole & present & present\\<br /> 2 & zero & zero & absent & absent\\<br /> 3 & pole & zero & preset & absent\\<br /> 4 & zero & pole & absent & presetnt<br />\end{array}$ また、Foster第一形式と第二形式は互いに逆の関係にあるので、同じ等価回路で一方が極をとるときその逆数は零点となり、その逆も真なりで、以下の対応関係が存在する。 $\begin{array}<br />first Foster form & second Foster form\\ 1 & 2\\ 2 & 1\\ 3 & 4\\ 4 & 3\end{array}$ 問題の回路はω=0に零点、ω=∞に極を持つので、第一Foster形のcase 4に該当する。第二Foster形では零点と極が逆になるcase 3が等価対応する形となる。従って回路図に描くとということになる。一方Cauer展開に関しても同様に以下のことを既に知っている。引用：第一Cauer形の場合 $\begin{array}<br />Case & \omega=0 & \omega=\infty & First element & Last element\\ 1 & pole & pole & L & C\\<br /> 2 & zero & zero & C & L\\<br /> 3 & pole & zero & C & C\\<br /> 4 & zero & pole & L & L<br />\end{array}$ 第二Cauer形の場合 $\begin{array}<br />Case & \omega=0 & \omega=\infty & First element & Last element\\<br /> 1 & pole & pole & L & C\\<br /> 2 & zero & zero & C & L\\<br /> 3 & pole & zero & C & C\\<br /> 4 & zero & pole & L & L<br />\end{array}$ ということになる。従って与えられた回路からω=0が零点、ω=∞が極である等価な第一Cauer展開形はLが直列、Cが並列接続され最初の素子と最後の素子が共にLとなりということになる。同様に第二Cauer展開形はLが並列、Cが直列で最初の素子と最後の素子が共にLとなりということになる。次ぎの回路は少々ひねってある。一見すると第二Cauer形に見えるが最後の素子が２つのCの直列になっている。これはブービートラップみたいなひっかけで、教科書暗記式で問題に臨もうとするやからを排除するための問題である。賢明な読者ならもうお分かりの通り、最後のC4とC5はキャパシタンスを直列に接続した合成キャパシタンスとして一個の等価Cと見なすことができる。従って第一素子がLで最終素子がCなので、第二Cauer形のcase 2に該当する。ω=0,∞が共に零点であることからもそれとわかる。従って第一Cauer形ではLが直列接続、Cが並列接続となり第一素子がCで最終素子がLなのでということになる。同様に第一Foster展開でω=0,∞が共に零点であるcaseではC0,L∞が存在しないのでLC並列回路の直列接続のみとなりということになる。第二Foster展開ではω=0,∞あ共に極となるcaseが対応するのでL0,C∞が共に存在しということになる。ちょっと気になるのが、第一Foster形ではLC並列回路が２つあったのに、第二Foster形ではLC直列回路がひとつしか現れない点である。疑問に思われるのは当然であるので、確かめてみよう。第一Foster形の回路からリアクタンス関数の式を起こすと $\begin{array}<br />Z(s)&=&\frac{1}{\frac{1}{s\,L_2}+s\,C_2}+\frac{1}{\frac{1}{s\,L_1}+s\,C_1}\\<br />&=&\left(\frac{C_1+C_2}{C_1 C_2}\right)\frac{s\,\left( {s}^{2}+\frac{L_1+L_2}{\left(C_1+C_2\right)L_1 L_2}\right) }{\left(s^2+\frac{1}{C_1 L_1}\right)\left(s^2+\frac{1}{C_2 L_2}\right)}<br />\end{eqnarray}$ これを第二Foster形に展開するためにアドミッタンスの総和に部分分数展開すると $\begin{array}<br />Y(s)&=&\frac{1}{Z(s)}\\<br />&=&\left(\frac{C_1 C_2}{C_1+C_2}\right)\frac{\left(s^2+\frac{1}{C_1 L_1}\right)\left(s^2+\frac{1}{C_2 L_2}\right)}{s\,\left( {s}^{2}+\frac{L_1+L_2}{\left(C_1+C_2\right)L_1 L_2}\right) }\\<br />&=&\left(\frac{C_1 C_2}{C_1+C_2}\right)\left(s+\frac{C_1+C_2}{s\,C_1 C_2\left( L1+L2\right)\left(\right)}+\frac{s\,\left( {C2}\,{L2}-{C1}^\,{L1}\right)^2 }{C_1 C_2 L_1 L_2\left( L_1+L_2\right)\left(C_1+C_2\right)\,\left( {s}^{2}+\frac{L_1+L_2}{L_1 L_2\left(C_1+C_2\right)}\right) }\right)\\<br />&=&L_0 s+\frac{1}{C_\infty s}+\frac{1}{C_1 s+\frac{1}{L_1 s}}<br />\end{eqnarray}$ ということで間違いではない。良く考えれば当然だが、第三項は誘導性か容量性かどちらかのアドミッタンス値（正か負のいずれか）をとる。一方L0とC∞のアドミッタンスの総和も誘導性か容量性のいずれかのアドミッタンス値をとり、全部を足すとゼロになる条件が第三項が誘導性か容量性かによって2ケース存在することになる。これが第一Foster形が持つ２つの極の双対となる零点となるのだった。

webadm	投稿日時: 2010-4-20 4:22
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3094	【18】続々：リアクタンス回路の合成次ぎは少しひねったリアクタンス回路の合成問題。極と零点と、スケーリングファクタの代わりに零点における微係数が与えられている点が前問と異なる。極は ω2=2000[rad/sec] ω4=4000[rad/sec] 零点は ω3=3000[rad/sec] 零点における微係数 dX/dω=4/7[Ω/rad/sec] というもの。 0＜ω2＜ω3＜ω4＜∞ なる関係から、他にω=0、∞に零点を持つことが明らか。従って以下の様なリアクタンス関数の形になるはず。 $Z(s)=H\frac{s\left(s^2+{\omega_3}^2\right)}{\left(s^2+{\omega_2}^2\right)\left(s^2+{\omega_4}^2\right)}$ スケーリングファクタHは $\begin{eqnarray}<br />\lim_{\omega\to\omega_3}\frac{dX(\omega)}{d\omega}&=&\lim_{\omega\to\omega_3}\frac{d}{d\omega}Im\left(Z(j\omega)\right)\\<br />&=&\lim_{\omega\to\omega_3}\frac{d}{d\omega}Im\left(H\frac{j\omega\left(-{\omega}^2+{\omega_3}^2\right)}{\left(-{\omega}^2+{\omega_2}^2\right)\left(-{\omega}^2+{\omega_4}^2\right)}\right)\\<br />&=&\lim_{\omega\to\omega_3}\frac{d}{d\omega}H\frac{\omega\left( {\omega_3}^{2}-{\omega}^{2}\right)}{\left( {\omega_2}^{2}-{\omega}^{2}\right) \,\left( {\omega_4}^{2}-{\omega}^{2}\right) }\\<br />&=&\left.H\left(\frac{\left( {\omega_3}^{2}-{\omega}^{2}\right)}{\left( {\omega_2}^{2}-{\omega}^{2}\right) \,\left( {\omega_4}^{2}-{\omega}^{2}\right) }+\frac{2\,{\omega}^{2}\,\left( {\omega_3}^{2}-{\omega}^{2}\right)}{{\left( {\omega_2}^{2}-{\omega}^{2}\right) }^{2}\,\left( {\omega_4}^{2}-{\omega}^{2}\right) }-\frac{2\,{\omega}^{2}}{\left( {\omega_2}^{2}-{\omega}^{2}\right) \,\left( {\omega_4}^{2}-{\omega}^{2}\right) }+\frac{2\,{\omega}^{2}\,\left( {\omega_3}^{2}-{\omega}^{2}\right)}{\left( {\omega_2}^{2}-{\omega}^{2}\right) \,{\left( {\omega_4}^{2}-{\omega}^{2}\right) }^{2}}\right)\right\|_{\omega=\omega_3}\\<br />&=&-H\frac{2\,{\omega_3}^{2}}{\left( {\omega_2}^{2}-{\omega_3}^{2}\right) \,\left( {\omega_4}^{2}-{\omega_3}^{2}\right) }\\<br />&=&-H\frac{2\cdot{3000}^{2}}{\left( {2000}^{2}-{3000}^{2}\right) \,\left( {4000}^{2}-{3000}^{2}\right) }\\<br />&=&H\frac{9}{17500000}\\<br />&=&\frac{4}{7}\\<br />H&=&\frac{10000000}{9}<br />\end{eqnarray}$ 従って最終的なリアクタンス関数は $Z(s)=\left(\frac{10000000}{9}\right)\frac{s\left(s^2+{\omega_3}^2\right)}{\left(s^2+{\omega_2}^2\right)\left(s^2+{\omega_4}^2\right)}$ ということになる。これを第一Foster展開すると $\begin{eqnarray}<br />Z(s)&=&\left(\frac{10000000}{9}\right)\frac{s\left(s^2+{\omega_3}^2\right)}{\left(s^2+{\omega_2}^2\right)\left(s^2+{\omega_4}^2\right)}\\<br />&=&\frac{H_1 s}{\left(s^2+{\omega_2}^2\right)}+\frac{H_2 s}{\left(s^2+{\omega_4}^2\right)}\\<br />&=&\frac{1}{C_1 s+\frac{1}{L_1 s}}+\frac{1}{C_2 s+\frac{1}{L_2 s}}\\<br />C_1&=&\frac{1}{H_1}=\frac{27}{12500000}=2.16\,[\mu F]\\<br />L_1&=&\frac{H_1}{{\omega_2}^2}=\frac{12500000}{27\cdot 2000^2}=115.7\,[mH]\\<br />C_2&=&\frac{1}{H_2}=\frac{27}{17500000}=1.543\,[\mu F]\\<br />L_2&=&\frac{H_2}{{\omega_4}^2}=\frac{17500000}{27\cdot 4000^2}=40.5\,[mH]\\<br />H_1&=&\lim_{s^2\to-{\omega_2}^2}\frac{\left(s^2+{\omega_2}^2\right)Z(s)}{s}\\<br />&=&\left.\left(\frac{10000000}{9}\right)\frac{\left(s^2+{\omega_3}^2\right)}{\left(s^2+{\omega_4}^2\right)}\right\|_{s^2=-{\omega_2}^2}\\<br />&=&\left(\frac{10000000}{9}\right)\frac{\left(-{\omega_2}^2+{\omega_3}^2\right)}{\left(-{\omega_2}^2+{\omega_4}^2\right)}\\<br />&=&\left(\frac{10000000}{9}\right)\frac{\left(-2000^2+3000^2\right)}{\left(-2000^2+4000^2\right)}\\<br />&=&\frac{12500000}{27}\\<br />H_2&=&\lim_{s^2\to-{\omega_4}^2}\frac{\left(s^2+{\omega_4}^2\right)Z(s)}{s}\\<br />&=&\left.\left(\frac{10000000}{9}\right)\frac{\left(s^2+{\omega_3}^2\right)}{\left(s^2+{\omega_2}^2\right)}\right\|_{s^2=-{\omega_4}^2}\\<br />&=&\left(\frac{10000000}{9}\right)\frac{\left(-{\omega_4}^2+{\omega_3}^2\right)}{\left(-{\omega_4}^2+{\omega_2}^2\right)}\\<br />&=&\left(\frac{10000000}{9}\right)\frac{\left(-4000^2+3000^2\right)}{\left(-4000^2+2000^2\right)}\\<br />&=&\frac{17500000}{27}\\<br />\end{eqnarray}$ ということになる。回路図に描くとということになる。

webadm	投稿日時: 2010-4-19 10:09
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3094	【17】続：リアクタンス回路の合成ここからしばらくリアクタンス回路の合成問題が続く。次ぎの問題は与えられた周波数特性を満足するリアクタンス一端子対回路を（１）並列共振回路の直列接続（第一Foster展開）（２）直列共振回路の並列接続（第二Foster展開）（３）はしご形かいろ（Cauer展開）で合成せよというもの。与えられる周波数特性は H(スケーリングファクタ）は0.2 共振角周波数ω1=1000[rad/sec]、ω3=3000[rad/sec] 反共振角周波数ω2=2000[rad/sec] とする。問題文にはスケーリングファクタの単位が[H]とか誤って記載されているが、スケーリングファクタは無次元なので単位などないので明らかに著者の誤記。周波数特性で重要となるω=0と∞が零点なのか極なのかが与えられていないが、与えられた零点と極の関係から 0＜ω1＜ω2＜ω3＜∞ となるので、リアクタンス関数は零点と極が交互に位置しているのでω1とω3が零点でω2が極であるのでω=0とω=∞は極であることは自明。となるとすべての特異点が明らかになり、スケーリングファクタも与えられているのでリアクタンス関数は以下の通りとなる。 $\begin{eqnarray}<br />Z(s)&=&H\frac{\left(s^2+{\omega_1}^2\right)\left(s^2+{\omega_3}^2\right)}{s\left(s^2+{\omega_2}^2\right)}\\<br />&=&0.2\frac{\left(s^2+1000^2\right)\left(s^2+3000^2\right)}{s\left(s^2+2000^2\right)}<br />\end{eqnarray}$ リアクタンス関数が定まれば回路合成が出来るので。第一Foster展開をすると $\begin{eqnarray}<br />Z(s)&=&0.2\frac{\left(s^2+1000^2\right)\left(s^2+3000^2\right)}{s\left(s^2+2000^2\right)}\\<br />&=&\frac{H_0}{s}+\frac{H_1 s}{s^2+2000^2}+H_\infty s\\<br />&=&\frac{1}{C_0 s}+\frac{1}{C_1 s+\frac{1}{L_1 s}}+L_\infty s\\<br />C_0&=&\frac{1}{H_0}=\frac{1}{450000}=2.22\,[\mu F]\\<br />C_1&=&\frac{1}{H_1}=\frac{1}{750000}=1.33\,[\mu H]\\<br />L_1&=&\frac{H_1}{2000^2}=\frac{750000}{2000^2}=187.5\,[mH]\\<br />L_\infty&=&H_\infty=0.2\,[H]\\<br />H_0&=&\lim_{s^2\to0}sZ(s)=\left.0.2\frac{\left(s^2+1000^2\right)\left(s^2+3000^2\right)}{\left(s^2+2000^2\right)}\right\|_{s^2=0}\\<br />&=&0.2\frac{\left(1000^2\right)\left(3000^2\right)}{\left(2000^2\right)}\\<br />&=&450000\\<br />H_1&=&\lim_{s^2\to-2000^2}\frac{\left(s^2+2000^2\right)Z(s)}{s}=\left.0.2\frac{\left(s^2+1000^2\right)\left(s^2+3000^2\right)}{s^2}\right\|_{s^2=-2000^2}\\<br />&=&0.2\frac{\left(-2000^2+1000^2\right)\left(-2000^2+3000^2\right)}{-2000^2}\\<br />&=&750000\\<br />H_\infty&=&\lim_{s^2\to\infty}\frac{Z(s)}{s}=\left.0.2\frac{\left(s^2+1000^2\right)\left(s^2+3000^2\right)}{s^2\left(s^2+2000^2\right)}\right\|_{s^2=\infty}\\<br />&=&\left.0.2\frac{\left(1+\frac{1000^2}{s^2}\right)\left(1+\frac{3000^2}{s^2}\right)}{\left(1+\frac{2000^2}{s^2}\right)}\right\|_{s^2=\infty}\\<br />&=&0.2<br />\end{eqnarray}$ 回路図で表すと次ぎに第二Foster展開はアドミッタンスの総和に部分分数展開すればよいので $\begin{eqnarray}<br />Y(s)&=&\frac{1}{Z(s)}=\frac{s\left(s^2+2000^2\right)}{0.2\left(s^2+1000^2\right)\left(s^2+3000^2\right)}\\<br />&=&\frac{H_1 s}{s^2+1000^2}+\frac{H_2 s}{s^2+3000^2}\\<br />&=&\frac{1}{L_1 s+\frac{1}{C_1 s}}+\frac{1}{L_2 s+\frac{1}{C_2 s}}\\<br />L_1&=&\frac{1}{H_1}=\frac{1}{1.875}=533.3\,[mH]\\<br />C_1&=&\frac{H_1}{1000^2}=\frac{1.875}{1000^2}=1.875\,[\mu F]\\<br />L_2&=&\frac{1}{H_2}=\frac{1}{3.125}=320\,[mH]\\<br />C_2&=&\frac{H_2}{3000^2}=\frac{3.125}{3000^2}=0.3472\,[\mu F]\\<br />H_1&=&\lim_{s^2\to-1000^2}\frac{\left(s^2+1000^2\right)Y(s)}{s}=\left.\frac{\left(s^2+2000^2\right)}{0.2\left(s^2+3000^2\right)}\right\|_{s^2=-1000^2}\\<br />&=&\frac{\left(-1000^2+2000^2\right)}{0.2\left(-1000^2+3000^2\right)}\\<br />&=&1.875\\<br />H_2&=&\lim_{s^2\to-3000^2}\frac{\left(s^2+3000^2\right)Y(s)}{s}=\left.\frac{\left(s^2+2000^2\right)}{0.2\left(s^2+1000^2\right)}\right\|_{s^2=-3000^2}\\<br />&=&\frac{\left(-3000^2+2000^2\right)}{0.2\left(-3000^2+1000^2\right)}\\<br />&=&3.125<br />\end{eqnarray}$ 回路図で表すと最後にCauer展開。へそ曲がりで別解の第二Cauer展開でやってみよう。 $\begin{eqnarray}<br />Z(s)&=&0.2\frac{\left(s^2+1000^2\right)\left(s^2+3000^2\right)}{s\left(s^2+2000^2\right)}\\<br />&=&\frac{0.2s^4+0.2\left(1000^2+3000^2\right)s^2+0.2\left(1000^2\right)\left(3000^2\right)}{s^3+200^2s}\\<br />&=&\frac{0.2\left(1000^2\right)\left(3000^2\right)p^4+0.2\left(1000^2+3000^2\right)p^2+0.2}{2000^2p^3+p}\\<br />&=&\frac{0.2\left(1000^2\right)\left(3000^2\right)}{2000^2}p+\frac{\left(0.2\left(1000^2+3000^2\right)-\frac{0.2\left(1000^2\right)\left(3000^2\right)}{2000^2}\right)p^2+0.2}{2000^2p^3+p}\\<br />&=&450000p+\frac{1550000p^2+0.2}{2000^2p^3+p}\\<br />&=&450000p+\frac{1}{\Large\frac{2000^2}{1550000}p+\frac{\left(1-0.2\frac{2000^2}{1550000}\right)p}{1550000p^2+0.2}}\\<br />&=&450000p+\frac{1}{\Large\frac{80}{31}p+\frac{\frac{15}{31}p}{1550000p^2+0.2}}\\<br />&=&\frac{450000}{s}+\frac{1}{\Large\frac{80}{31s}+\frac{1}{\frac{9610000}{3s}+\frac{31}{75}s}}\\<br />&=&\frac{1}{C_1 s}+\frac{1}{\Large\frac{1}{L_2 s}+\frac{1}{\frac{1}{C_3 s}+L_4 s}}\\<br />C_1&=&\frac{1}{450000}=2.22\,[\mu F]\\<br />L_2&=&\frac{31}{80}=387.5\,[mH]\\<br />C_3&=&\frac{3}{9610000}=0.3122\,[\mu F]\\<br />L_4&=&\frac{31}{75}=413.3\,[mH]\\<br />p&=&s^{-1}<br />\end{eqnarray}$ 回路図で表すと

webadm	投稿日時: 2010-4-19 2:30
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3094	【16】リアクタンス回路の合成次ぎはお待ちかね（誰も待ってないって）リアクタンス回路の合成問題。以下のリアクタンス関数からFoster展開とCauer展開でそれぞれ２種類ずつ回路を合成せよというもの。 $Z_1(s)=\frac{\left(s^2+1\right)\left(s^2+9\right)}{s\left(s^2+4\right)}$ Foster展開はインピーダンスの総和へ部分分数展開する形とアドミッタンスの総和へ部分分数展開する形の２種類に合成できる。まずはインピーダンスの総和に部分分数展開してみよう。 $\begin{eqnarray}<br />Z_1(s)&=&\frac{K_0}{s}+\frac{K_1 s}{s^2+4}+K_\infty s\\<br />&=&\frac{1}{C_0 s}+\frac{1}{C_1 s+\frac{1}{L_1 s}}+L_\infty s\\<br />C_0&=&\frac{1}{K_0}=\frac{4}{9}\,[F]\\<br />C_1&=&\frac{1}{K_1}=\frac{4}{15}\,[H]\\<br />L_1&=&\frac{K_1}{4}=\frac{15}{16}\,[H]\\<br />L_\infty&=&K_\infty=1\,[H]\\<br />K_0&=&\lim_{s^2\to0}sZ_1(s)=\left.\frac{\left(s^2+1\right)\left(s^2+9\right)}{\left(s^2+4\right)}\right\|_{s^2=0}\\<br />&=&\frac{9}{4}\\<br />K_1&=&\lim_{s^2\to-4}\frac{\left(s^2+4\right)Z_1(s)}{s}=\left.\frac{\left(s^2+1\right)\left(s^2+9\right)}{s^2}\right\|_{s^2=-4}\\<br />&=&\frac{\left(-4+1\right)\left(-4+9\right)}{-4}\\<br />&=&\frac{15}{4}\\<br />K_\infty&=&\lim_{s^2\to\infty}\frac{Z_1(s)}{s}=\left.\frac{\left(s^2+1\right)\left(s^2+9\right)}{s^2\left(s^2+4\right)}\right\|_{s^2=\infty}\\<br />&=&\left.\frac{\left(1+\frac{1}{s^2}\right)\left(1+\frac{9}{s^2}\right)}{\left(1+\frac{4}{s^2}\right)}\right\|_{s^2=\infty}\\<br />&=&1<br />\end{eqnarray}$ 回路図を描くと同様にアドミッタンスの総和へ部分分数展開すると $\begin{eqnarray}<br />Y_1(s)&=&\frac{1}{Z_1(s)}=\frac{s\left(s^2+4\right)}{\left(s^2+1\right)\left(s^2+9\right)}\\<br />&=&\frac{K_1 s}{s^2+1}+\frac{K_2 s}{s^2+9}\\<br />&=&\frac{1}{L_1 s+\frac{1}{C_1 s}}+\frac{1}{L_2 s+\frac{1}{C_2 s}}\\<br />L_1&=&\frac{1}{K_1}=\frac{8}{3}\,[H]\\<br />C_1&=&K_1=\frac{3}{8}\,[F]\\<br />L_2&=&\frac{1}{K_2}=\frac{8}{5}\,[H]\\<br />C_2&=&\frac{K_2}{9}=\frac{5}{72}\,[F]\\<br />K_1&=&\lim_{s^2\to-1}\frac{\left(s^2+1\right)Y_1(s)}{s}\\<br />&=&\left.\frac{s^2+4}{s^2+9}\right\|_{s^2=-1}\\<br />&=&\frac{-1+4}{-1+9}\\<br />&=&\frac{3}{8}\\<br />K_2&=&\lim_{s^2\to-9}\frac{\left(s^2+9\right)Y_1(s)}{s}\\<br />&=&\left.\frac{s^2+4}{s^2+1}\right\|_{s^2=-9}\\<br />&=&\frac{-9+4}{-9+1}\\<br />&=&\frac{5}{8}<br />\end{eqnarray}$ 回路図を描くと今度はCauer展開。Cauer展開は次数の最も大きな項から割り出すのと次数の最も小さい項から割り出す２通りの形がある。まず次数の大きな項から割り出してみよう。 $\begin{eqnarray}<br />Z_1(s)&=&\frac{\left(s^2+1\right)\left(s^2+9\right)}{s\left(s^2+4\right)}\\<br />&=&\frac{s^4+10s^2+9}{s^3+4s}\\<br />&=&s+\frac{6s^2+9}{s^3+4s}\\<br />&=&s+\frac{1}{\Large\frac{1}{6}s+\frac{\left(4-\frac{9}{6}\right)s}{6s^2+9}}\\<br />&=&s+\frac{1}{\Large\frac{1}{6}s+\frac{1}{\frac{12}{5}s+\frac{1}{\frac{5}{18}s}}}\\<br />&=&L_1 s+\frac{1}{\Large C_2 s+\frac{1}{L_3 s+\frac{1}{C_4 s}}}\\<br />L_1&=&1\,[H]\\<br />C_2&=&\frac{1}{6}\,[F]\\<br />L_3&=&\frac{12}{5}\,[H]\\<br />C_4&=&\frac{5}{18}\,[F]\\<br />\end{eqnarray}$ 回路図を描くと今度は次数の最も少ない項から割り出すと $\begin{eqnarray}<br />Z_1(s)&=&\frac{\left(s^2+1\right)\left(s^2+9\right)}{s\left(s^2+4\right)}\\<br />&=&\frac{s^4+10s^2+9}{s^3+4s}\\<br />&=&\frac{9p^4+10p^2+1}{4p^3+p}\\<br />&=&\frac{9}{4}p+\frac{\left(10-\frac{9}{4}\right)p^2+1}{4p^3+p}\\<br />&=&\frac{9}{4}p+\frac{1}{\Large\frac{16}{31}p+\frac{\left(1-\frac{16}{31}\right)p}{\frac{31}{4}p^2+1}}\\<br />&=&\frac{9}{4}p+\frac{1}{\Large\frac{16}{31}p+\frac{1}{\frac{961}{60}p+\frac{31}{15p}}}\\<br />&=&\frac{9}{4s}+\frac{1}{\Large\frac{16}{31s}+\frac{1}{\frac{961}{60s}+\frac{31}{15}s}}\\<br />&=&\frac{1}{C_1 s}+\frac{1}{\Large\frac{1}{L_2 s}+\frac{1}{\frac{1}{C_3 s}+L_4 s}}\\<br />C_1&=&\frac{4}{9}\,[F]\\<br />L_2&=&\frac{31}{16}\,[H]\\<br />C_3&=&\frac{60}{961}\,[F]\\<br />L_4&=&\frac{31}{15}\,[H]\\<br />p&=&s^{-1}<br />\end{eqnarray}$ 回路図を描くと $Z_2(s)=\frac{\left(s^2+2\right)\left(s^2+6\right)}{s\left(s^2+4\right)}$ インピーダンスの総和に部分分数展開してみよう。 $\begin{eqnarray}<br />Z_2(s)&=&\frac{\left(s^2+2\right)\left(s^2+6\right)}{s\left(s^2+4\right)}\\<br />&=&\frac{K_0}{s}+\frac{K_1 s}{s^2+4}+K_\infty s\\<br />&=&\frac{1}{C_0 s}+\frac{1}{C_1 s+\frac{1}{L_1 s}}+L_\infty s\\<br />C_0&=&\frac{1}{K_0}=\frac{1}{3}\,[F]\\<br />C_1&=&\frac{1}{K_1}=1\,[F]\\<br />L_1&=&\frac{K_1}{4}=\frac{1}{4}\,[H]\\<br />L_\infty&=&K_\infty=1\,[H]\\<br />K_0&=&\lim_{s^2\to0}sZ_2(s)=\left.\frac{\left(s^2+2\right)\left(s^2+6\right)}{\left(s^2+4\right)}\right\|_{s^2=0}\\<br />&=&3\\<br />K_1&=&\lim_{s^2\to-4}\frac{\left(s^2+4\right)Z_2(s)}{s}=\left.\frac{\left(s^2+2\right)\left(s^2+6\right)}{s^2}\right\|_{s^2=-4}\\<br />&=&\frac{\left(-4+2\right)\left(-4+6\right)}{-4}\\<br />&=&1\\<br />K_\infty&=&\lim_{s^2\to\infty}\frac{Z_2(s)}{s}=\left.\frac{\left(s^2+2\right)\left(s^2+6\right)}{s^2\left(s^2+4\right)}\right\|_{s^2=\infty}\\<br />&=&\left.\frac{\left(1+\frac{2}{s^2}\right)\left(1+\frac{6}{s^2}\right)}{1+\frac{4}{s^2}}\right\|_{s^2=\infty}\\<br />&=&1<br />\end{eqnarray}$ 回路図を描くと同様にアドミッタンスの総和へ部分分数展開すると $\begin{eqnarray}<br />Y_2(s)&=&\frac{1}{Z_2(s)}=\frac{s\left(s^2+4\right)}{\left(s^2+2\right)\left(s^2+6\right)}\\<br />&=&\frac{K_1 s}{s^2+2}+\frac{K_2 s}{s^2+6}\\<br />&=&\frac{1}{C_1 s+\frac{1}{L_1 s}}+\frac{1}{C_2 s+\frac{1}{L_2 s}}\\<br />C_1&=&\frac{1}{K_1}=2\,[F]\\<br />L_1&=&\frac{K_1}{2}=\frac{1}{4}\,[H]\\<br />C_2&=&\frac{1}{K_2}=2\,[F]\\<br />L_2&=&\frac{K_2}{6}=\frac{1}{12}\,[H]\\<br />K_1&=&\lim_{s^2\to-2}\frac{\left(s^2+2\right)Y_2(s)}{s}\\<br />&=&\left.\frac{s^2+4}{s^2+6}\right\|_{s^2=-2}\\<br />&=&\frac{-2+4}{-2+6}\\<br />&=&\frac{1}{2}\\<br />K_2&=&\lim_{s^2\to-6}\frac{\left(s^2+6\right)Y_2(s)}{s}\\<br />&=&\left.\frac{s^2+4}{s^2+2}\right\|_{s^2=-6}\\<br />&=&\frac{-6+4}{-6+2}\\<br />&=&\frac{1}{2}\\<br />\end{eqnarray}$ 回路図を描くと今度はCauer展開。まず次数の大きな項から割り出してみよう。 $\begin{eqnarray}<br />Z_1(s)&=&\frac{\left(s^2+2\right)\left(s^2+6\right)}{s\left(s^2+4\right)}\\<br />&=&\frac{s^4+8s^2+12}{s^3+4s}\\<br />&=&s+\frac{4s^2+12}{s^3+4s}\\<br />&=&s+\frac{1}{\Large\frac{1}{4}s+\frac{\left(4-\frac{12}{4}\right)s}{4s^2+12}}\\<br />&=&s+\frac{1}{\Large\frac{1}{4}s+\frac{1}{4s+\frac{12}{s}}}\\<br />&=&L_1 s+\frac{1}{\Large C_2 s+\frac{1}{L_3 s+\frac{1}{C_4 s}}}\\<br />L_1&=&1\,[H]\\<br />C_2&=&\frac{1}{4}\,[F]\\<br />L_3&=&4\,[H]\\<br />C_4&=&\frac{1}{12}\,[F]<br />\end{eqnarray}$ 回路図を描くと今度は次数の最も少ない項から割り出すと $\begin{eqnarray}<br />Z_1(s)&=&\frac{\left(s^2+2\right)\left(s^2+6\right)}{s\left(s^2+4\right)}\\<br />&=&\frac{s^4+8s^2+12}{s^3+4s}\\<br />&=&\frac{12p^4+8p^2+1}{4p^3+p}\\<br />&=&3p+\frac{5p^2+1}{4p^3+p}\\<br />&=&3p+\frac{1}{\Large\frac{4}{5}p+\frac{\left(1-\frac{4}{5}\right)p}{5p^2+1}}\\<br />&=&3p+\frac{1}{\Large\frac{4}{5}p+\frac{1}{25p+\frac{5}{p}}}\\<br />&=&\frac{3}{s}+\frac{1}{\Large\frac{4}{5s}+\frac{1}{\frac{25}{s}+5s}}\\<br />&=&\frac{1}{C_1 s}+\frac{1}{\Large\frac{1}{L_2 s}+\frac{1}{\frac{1}{C_3 s}+L_4 s}}\\<br />C_1&=&\frac{1}{3}\,[F]\\<br />L_2&=&\frac{5}{4}\,[H]\\<br />C_3&=&\frac{1}{25}\,[F]\\<br />L_4&=&5\,[H]\\<br />p&=&s^{-1}<br />\end{eqnarray}$ 回路図を描くと

webadm	投稿日時: 2010-4-18 0:34
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3094	【15】続々：リアクタンス回路次ぎはリアクタンス回路の計算問題。以下の回路のリアクタンスとアドミッタンスを求めよというもの。回路図から駆動点インピーダンス関数の式を起こすと $\begin{eqnarray}<br />Z(s)&=&\frac{1}{\Large C_1 s+\frac{1}{\frac{1}{C_2 s}+L_1 s}+\frac{1}{L_2 s}}\\<br />&=&\frac{1}{\Large\frac{C_1 L_2 s^2+1}{L_2 s}+\frac{C_2 s}{C_2 L_1 s^2+1}}\\<br />&=&\frac{L_2 s\left(C_2 L_1 s^2+1\right)}{\left(C_1 L_2 s^2+1\right)\left(C_2 L_1 s^2+1\right)+C_2 L_2 s^2}\\<br />&=&\frac{L_2 s\left(C_2 L_1 s^2+1\right)}{C_1 C_2 L_1 L_2 s^4+\left(C_1 L_2 +C_2 L_1+C_2 L_2\right)s^2+1}\\<br />&=&\left(\frac{1}{C_1}\right)\frac{s\left(s^2+\frac{1}{C_2 L_1}\right)}{\left(s^4+\frac{C_1 L_2 +C_2 L_1+C_2 L_2}{C_1 C_2 L_1 L_2}s^2+\frac{1}{C_1 C_2 L_1 L_2}\right)}<br />\end{eqnarray}$ 従ってリアクタンスはインピーダンスの虚数部なので $\begin{eqnarray}<br />X(\omega)&=&Im(Z(j\omega))\\<br />&=&Im(\left(\frac{1}{C_1}\right)\frac{j\omega\left(-\omega^2+\frac{1}{C_2 L_1}\right)}{\left(\omega^4-\frac{C_1 L_2 +C_2 L_1+C_2 L_2}{C_1 C_2 L_1 L_2}\omega^2+\frac{1}{C_1 C_2 L_1 L_2}\right)})\\<br />&=&\left(\frac{1}{C_1}\right)\frac{\omega\left(\frac{1}{C_2 L_1}-\omega^2\right)}{\left(\omega^4-\frac{C_1 L_2 +C_2 L_1+C_2 L_2}{C_1 C_2 L_1 L_2}\omega^2+\frac{1}{C_1 C_2 L_1 L_2}\right)}<br />\end{eqnarray}$ で表され。それぞれの素子定数を代入すると $\begin{eqnarray}<br />X(\omega)&=&\frac{\omega\left(25-\omega^2\right)}{\left(\omega^4-26.58\omega^2+8.33\right)}<br />\end{eqnarray}$ 分母の式は更に因数分解可能だが式が複雑になるのでそのままにしている。アドミッタンスはインピーダンスの逆数なので $\begin{eqnarray}<br />Y(j\omega)&=&\frac{1}{Z(j\omega)}\\<br />&=&C_1\frac{\left(\omega^4-\frac{C_1 L_2 +C_2 L_1+C_2 L_2}{C_1 C_2 L_1 L_2}\omega^2+\frac{1}{C_1 C_2 L_1 L_2}\right)}{j\omega\left(-\omega^2+\frac{1}{C_2 L_1}\right)}\\&=&jC_1\frac{\left(\omega^4-\frac{C_1 L_2 +C_2 L_1+C_2 L_2}{C_1 C_2 L_1 L_2}\omega^2+\frac{1}{C_1 C_2 L_1 L_2}\right)}{\omega\left(\omega^2-\frac{1}{C_2 L_1}\right)}\\<br />&=&j\frac{\left(\omega^4-26.58\omega^2+8.33\right)}{\omega\left(\omega^2-25\right)}<br />\end{eqnarray}$ この回路のリアクタンスをプロットしてみると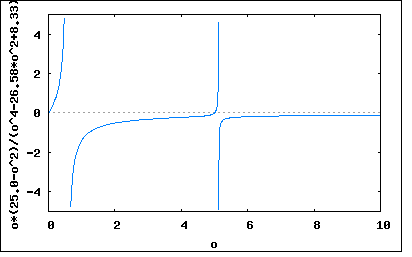アドミッタンスはちょうど零点と極が逆になった形になる。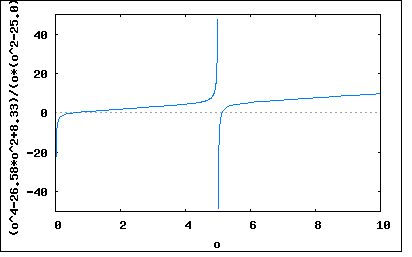回路図から駆動点インピーダンス関数の式を起こすと $\begin{eqnarray}<br />Z(s)&=&\frac{1}{\Large\frac{1}{\frac{1}{C_1 s}+L_1 s}+\frac{1}{\frac{1}{C_2 s}+L_2 s}+\frac{1}{L_3 s}}\\<br />&=&\frac{1}{\Large\frac{C_1 s}{1+C_1 L_1 s^2}+\frac{C_2 s}{1+C_2 L_2 s^2}+\frac{1}{L_3 s}}\\<br />&=&\frac{L_3 s\left(1+C_1 L_1 s^2\right)\left(1+C_2 L_2 s^2\right)}{C_1 L_3 s^2\left(1+C_2 L_2 s^2\right)+C_2 L_3 s^2\left(1+C_1 L_1 s^2\right)+\left(1+C_1 L_1 s^2\right)\left(1+C_2 L_2 s^2\right)}\\<br />&=&\frac{L_3 s\left(1+C_1 L_1 s^2\right)\left(1+C_2 L_2 s^2\right)}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)s^4+\left(C_1 L_3+C_2 L_3+C_1 L_1+C_2 L_2\right)s^2+1}\\<br />&=&\left(\frac{L_1 L_2 L_3}{L_2 L_3+L_1 L_3+L_1 L_2}\right)\frac{s\left(s^2+\frac{1}{C_1 L_1}\right)\left(s^2+\frac{1}{C_2 L_2}\right)}{\left(s^4+\frac{C_1 L_3+C_2 L_3+C_1 L_1+C_2 L_2}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}s^2+\frac{1}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}\right)}<br />\end{eqnarray}$ 従ってリアクタンスはインピーダンスの虚数部なので $\begin{eqnarray}<br />X(\omega)&=&Im(Z(j\omega))\\<br />&=&Im(\left(\frac{L_1 L_2 L_3}{L_2 L_3+L_1 L_3+L_1 L_2}\right)\frac{j\omega\left(-{\omega}^2+\frac{1}{C_1 L_1}\right)\left(-{\omega}^2+\frac{1}{C_2 L_2}\right)}{\left({\omega}^4-\frac{C_1 L_3+C_2 L_3+C_1 L_1+C_2 L_2}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}{\omega}^2+\frac{1}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}\right)})\\<br />&=&\left(\frac{L_1 L_2 L_3}{L_2 L_3+L_1 L_3+L_1 L_2}\right)\frac{\omega\left(\frac{1}{C_1 L_1}-\omega^2\right)\left(\frac{1}{C_2 L_2}-\omega^2\right)}{\left(\omega^4-\frac{C_1 L_3+C_2 L_3+C_1 L_1+C_2 L_2}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}\omega^2+\frac{1}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}\right)}<br />\end{eqnarray}$ で表され。それぞれの素子定数を代入すると $\begin{eqnarray}<br />X(\omega)&=&0.11538\frac{\omega\left(66.667-\omega^2\right)\left(166.67-\omega^2\right)}{\left(\omega^4-153.85\omega^2+4273.5\right)}<br />\end{eqnarray}$ 分母の式は更に因数分解可能だが式が複雑になるのでそのままにしている。アドミッタンスはインピーダンスの逆数なので $\begin{eqnarray}<br />Y(j\omega)&=&\frac{1}{Z(j\omega)}\\<br />&=&\left(\frac{L_2 L_3+L_1 L_3+L_1 L_2}{L_1 L_2 L_3}\right)\frac{\left({\omega}^4-\frac{C_1 L_3+C_2 L_3+C_1 L_1+C_2 L_2}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}{\omega}^2+\frac{1}{C_1 C_2\left(L_2 L_3+L_1 L_3+L_1 L_2\right)}\right)}{j\omega\left(-{\omega}^2+\frac{1}{C_1 L_1}\right)\left(-{\omega}^2+\frac{1}{C_2 L_2}\right)}\\<br />&=&j8.6667\frac{\left(\omega^4-153.85\omega^2+4273.5\right)}{\omega\left(\omega^2-66.667\right)\left(166.67-\omega^2\right)}<br />\end{eqnarray}$ この回路のリアクタンスをプロットしてみると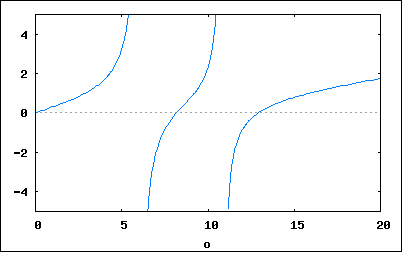アドミッタンスはちょうど零点と極が逆になった形になる。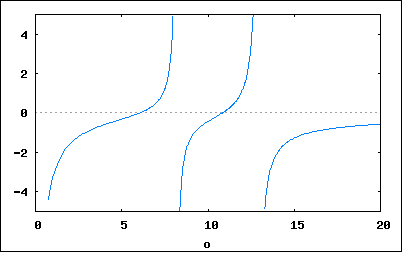

webadm	投稿日時: 2010-4-17 23:35
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3094	【14】相互インダクタンスを含むリアクタンス回路次ぎは理論の時には出てこなかった相互インダクタンスを伴うリアクタンス回路に関する問題。以下の回路の共振点と反共振点を求めよというもの。ただしL1,L2>M^2とする。相互インダクタンスを伴う等価回路に書き直すとということになる。上記の回路から駆動点インピーダンス関数の式を起こすと $\begin{eqnarray}Z(s)&=&\left(L_1-M\right)s+\frac{1}{\frac{1}{\left(L_2-M\right)s+\frac{1}{C s}}+\frac{1}{M s}}\\&=&\left(L_1-M\right)s+\frac{1}{\frac{C s}{C\left(L_2-M\right)s^2+1}+\frac{1}{M s}}\\&=&\left(L_1-M\right)s+\frac{M s\left(C\left(L_2-M\right)s^2+1\right)}{\cancel{C M s^2}+C\left(L_2-\cancel{M}\right)s^2+1}\\&=&\frac{\left(C L_2 s^2+1\right)\left(L_1-M\right)s+M s\left(C\left(L_2-M\right)s^2+1\right)}{C L_2 s^2+1}\\&=&\frac{s\left(\left(C L_2 s^2+1\right)\left(L_1-M\right)+M \left(C\left(L_2-M\right)s^2+1\right)\right)}{C L_2 s^2+1}\\&=&\frac{s\left(C L_1 L_2 s^2+L_1-\cancel{M C L_2 s^2}-\cancel{M}+\cancel{M C L_2 s^2}-M^2 C s^2+\cancel{M}\right)}{C L_2 s^2+1}\\&=&\frac{s\left(C \left(L_1 L_2-M^2\right) s^2+L_1\right)}{C L_2 s^2+1}\\&=&\left(\frac{L_1 L_2-M^2}{L_2}\right)\frac{s\left( s^2+\frac{L_1}{C \left(L_1 L_2-M^2\right)}\right)}{ \left(s^2+\frac{1}{C L_2}\right)}\\&=&H\frac{s\left(s^2+{\omega_3}^2\right)}{\left(s^2+{\omega_2}^2\right)}\\H&=&\frac{L_1 L_2-M^2}{L_2}\\\omega_2&=&\frac{1}{\sqrt{C L_2}}\\\omega_3&=&\sqrt{\frac{L_1}{C \left(L_1 L_2-M^2\right)}}=\frac{1}{\sqrt{C\left(\frac{L_1 L_2-M^2}{L_1}\right)}\end{eqnarray}$ 従って零点（共振点）にω=0,ω3、極（反共振点）にω=ω2、∞を持つということになる。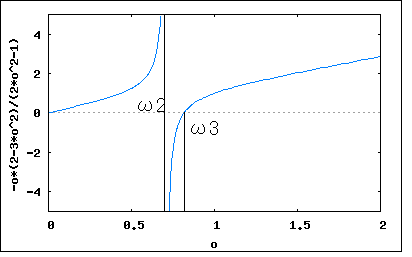

« 1 (2) 3 4 »

スレッド表示 | 古いものから

前のトピック | 次のトピック | トップ

投稿するにはまず登録を