Gan's blog - フォーラム

メイン > > 電気回路理論おもちゃ箱 > 2端子対回路演習問題

投稿者	スレッド
webadm	投稿日時: 2011-4-22 9:38
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3113	続々：最小位相推移回路遂に迎えた二端子対回路の最後の演習問題やはり最小位相推移に関するものである。以下の回路が最小位相推移回路か？というもの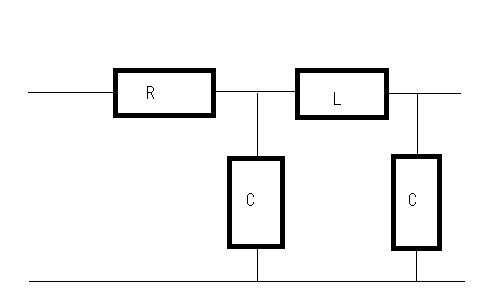ストラテジーとしては何らかの伝達イミッタンスを求めればいいのだが、著者の回答のように伝送行列を求めてそこからインピーダンス行列の伝達イミッタンス要素を逆算するのではない方法でやってみよう。基本的にこの程度の素子数であればマトリックスを使わずともキルヒホッフの法則と複素周波数を使って伝達イミッタンスを導くことができるはずである。ちょっと見通しはわるいが基本伝送回路と伝送行列の対応をすぐに思い出せない時には原始的な回路解析は面倒だが万能である。受動素子だけできているため相反回路でありインピーダンス行列は対称行列となるはずであるのでZ12,Z21どちらの伝達イミッタンスを求めても同じはずである。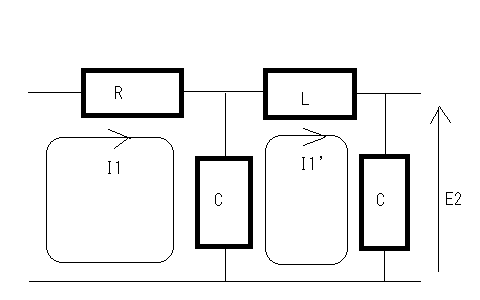以下の関係が成り立つ $\begin{eqnarray}<br />\frac{I_1-I^{\'}_1}{C s}&=&I^{\'}_1\left(L s+\frac{1}{C s}\right)\\<br />\frac{I^{\'}_1}{C s}&=&E_2<br />\end{eqnarray}$ 第一の式の両辺にCsを乗じて分母を払いI1'を導いて第二の式に代入すると $\begin{eqnarray}<br />I_1-I^{\'}_1&=&I^{\'}_1\left(C L s^2+1\right)\\<br />I_1&=&I^{\'}_1\left(C L s^2+2\right)\\<br />I^{\'}_1&=&\frac{I_1}{C L s^2+2}\\<br />\frac{I^{\'}_1}{C s}&=&\frac{I_1}{C s\left(C L s^2+2\right)}\\<br />&=&E_2<br />\end{eqnarray}$ 従って開放伝達インピーダンスは $\begin{eqnarray}<br />Z_{21}&=&\left.\frac{E_2}{I_1}\right\|_{I_2=0}=\frac{1}{C s\left(C L s^2+2\right)}<br />\end{eqnarray}$ ということになる。おろ、著者の解と全く違うのだがどちらかが間違っていることになる。どうやら著者が求めているのは伝達インピーダンスではなく伝達アドミッタンスだということがFパラメータからZパラメータを求めている式が実はYパラメータへの変換式であることから明らかである。それにE2はI1とLとCだけで決まりRには左右されないので式にRが現れるのは明らかに間違いである。 YパラメータはZパラメータの逆行列の要素であるため伝達アドミッタンスは伝達インピーダンスの単純な逆数ではないことに注意が必要である。これはわざと読者のために間違っているのかどうか真偽は定かではない。それではキルヒホッフの法則だけで短絡伝達アドミッタンスを求めてみよう。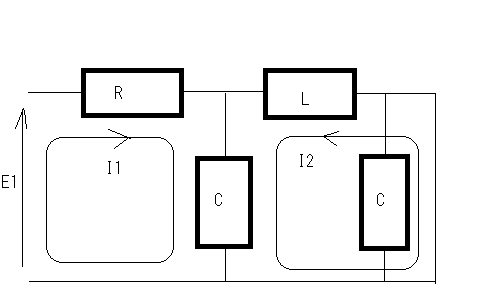以下の関係式が成り立つ $\begin{eqnarray}<br />E_1&=&I_1 R+\frac{I_1+I_2}{C s}\\<br />\frac{I_1+I_2}{C s}+I_2 L s&=&0<br />\end{eqnarray}$ 今度は第二の式の両辺にCsを乗じて分母を払いI1を求めて第一の式に代入すると $\begin{eqnarray}<br />I_1+I_2+I_2 C L s^2&=&0\\<br />I_1&=&-I_2\left(C L s^2+1\right)\\<br />E_1&=&-I_2 R\left(C L s^2+1\right)+\frac{-I_2\left(C L s^2+1\right)+I_2}{C s}\\<br />&=&-I_2\left(R\left(C L s^2+1\right)+L s\right)<br />\end{eqnarray}$ 従って短絡伝達アドミッタンスは $\begin{eqnarray}<br />Y_{21}&=&\left.\frac{I_2}{E_1}\right\|_{E_2=0}=-\frac{1}{R\left(C L s^2+1\right)+L s}<br />\end{eqnarray}$ ということになる。これは著者の解と同じであることから著者が導いたのは伝達インピーダンスではなく伝達アドミッタンスであったことが明らかである。このようにキルヒホッフの法則を求めたい電圧と電流の関係式がより簡単になるように適切に閉路電流を定めると簡単に回路は解析できることになる。もちろん前提として線形回路であることが必要だが、特定の動作範囲に限れば線形近似によって能動素子を含む電子回路にも応用できる。さて本題の最小位相推移回路かどうかという点であるが、伝達イミッタンスの式を因数分解してみると $\begin{eqnarray}<br />Z_{21}&=&\frac{1}{C s\left(C L s^2+2\right)}\\<br />&=&\frac{1}{C^2 L s\left(s^2+\frac{2}{C L}\right)}\\<br />&=&\frac{1}{C^2 L s\left(s-j\sqrt{\frac{2}{C L}}\right)\left(s+j\sqrt{\frac{2}{C L}}\right)}<br />\end{eqnarray}$ 従って極がs=0,±j√2/√CLとすべて虚軸上にありかつ一位なのと右半平面に零点をもたないので最小位相推移回路である。一方短絡伝達アドミッタンスは $\begin{eqnarray}<br />Y_{21}&=&-\frac{1}{R\left(C L s^2+1\right)+L s}\\<br />&=&-\frac{1}{R C L\left(s^2+\frac{1}{R C}s+\frac{1}{C L}\right)}\\<br />&=&-\frac{1}{R C L\left(\left(s+\frac{1}{2 R C}\right)^2+\frac{1}{C L}-\left(\frac{1}{2 R C}\right)^2\right)}\\<br />&=&-\frac{1}{R C L\left(\left(s+\frac{1}{2 R C}\right)^2-\left(\frac{1}{\left(2 R C\right)^2}-\frac{1}{C L}\right)\right)}\\<br />&=&-\frac{1}{R C L\left(\left(s+\frac{1}{2 R C}\right)^2-\left(\frac{C L-4 R^2 C^2}{C L\left(2 R C\right)^2}\right)\right)}\\<br />&=&-\frac{1}{R C L\left(\left(s+\frac{1}{2 R C}\right)^2-\left(\frac{L^2-4 R^2 C L}{L^2\left(2 R C\right)^2}\right)\right)}\\<br />&=&-\frac{1}{R C L\left(\left(s+\frac{1}{2 R C}\right)^2-\left(\frac{\sqrt{L^2-4 R^2 C L}}{2 R L C}\right)^2\right)}\\<br />&=&-\frac{1}{R C L\left(\left(s+\frac{1}{2 R C}+\frac{\sqrt{L^2-4 R^2 C L}}{2 R L C}\right)\left(s+\frac{1}{2 R C}-\frac{\sqrt{L^2-4 R^2 C L}}{2 R L C}\right)\right)}\\<br />&=&-\frac{1}{R C L\left(\left(s+\frac{L+\sqrt{L^2-4 R^2 C L}}{2 R L C}\right)\left(s+\frac{L-\sqrt{L^2-4 R^2 C L}}{2 R L C}\right)\right)}<br />\end{eqnarray}$ と因数分解されるので極は $\begin{eqnarray}<br />s&=&-\frac{L\pm\sqrt{L^2-4 R^2 C L}}{2 R L C}<br />\end{eqnarray}$ ということで左半平面にのみ存在し一位なので最小位相推移回路である。ここで根軌跡法を思い出してみると、極の軌跡は以下の様な(不定）方程式の解の集合である。ただしsは複素数だがR,L,Cは正の実数である $\begin{eqnarray}<br />F\left(s, L, R, C\right)&=&\left(s+\frac{L+\sqrt{L^2-4 R^2 C L}}{2 R L C}\right)\left(s+\frac{L-\sqrt{L^2-4 R^2 C L}}{2 R L C}\right)=0<br />\end{eqnarray}$ よく見るとR,L,Cの大小関係によっては極が右半平面に現れることがありそうにも見える。極が右半平面に現れないためには極が実軸上に限る場合 $\begin{eqnarray}<br />L-\sqrt{L^2-4 R^2 C L}\ge 0\,\,\left{L^2-4 R^2 C L\ge 0\right}\\<br />\sqrt{\frac{L}{C}}\ge \sqrt{\frac{L}{C}-4 R^2}\,\,\left{\sqrt{\frac{L}{C}}\ge 2R\right}<br />\end{eqnarray}$ という興味深い関係式が得られる。R,L,Cはいずれも正の実数であるから、極が実軸上にある限り常にこの関係は成立する他方極が複素数の場合を考えるともっと簡単で $\begin{eqnarray}<br />L^2-4 R^2 C L\lt 0\\<br />\sqrt{\frac{L}{C}}\lt 2 R<br />\end{eqnarray}$ となる。極が複素数の場合、極の実数部は-L/2RLCとなるためである。これは実に面白い。別の機会に改めて研究してみよう。これらを見ると伝達イミッタンスは分子と分母の次数の差が2以上のものがあることになる。時間があればこれらのベクトル軌跡を描いてみるとおもしろいかもしれない。それは読者の課題としてこれにて二端子対回路演習問題を終えよう。 P.S この問題の回路でR,L,Cが受動素子の場合はすべて正の実数をとるため最小位相推移回路となるが、トランジスタやオペアンプなどを使用して能動素子を使うと負のR,L,C値を持つことができるようになり、非最小位相推移回路が出来てしまう。その場合、不安定零点を持つようになるため、自己励起発振動作をするような回路も造りだせるようになる。受動素子だけでは延々に振動し続ける回路というのはできない。

フラット表示

前のトピック | 次のトピック

題名	投稿者	日時
2端子対回路演習問題	webadm	2010-5-20 4:53
インピーダンスパラメータ	webadm	2010-5-20 5:54
インピーダンスパラメータとアドミッタンスパラメータ	webadm	2010-5-22 23:43
インピーダンスパラメータとハイブリッドパラメータ	webadm	2010-5-23 1:32
インピーダンス行列とアドミッタンス行列	webadm	2010-5-23 10:12
T形回路	webadm	2010-5-23 16:25
続：T形回路	webadm	2010-5-23 16:33
π形回路	webadm	2010-5-23 17:20
Zobel変換	webadm	2010-5-23 17:58
ハイブリッドパラメータ	webadm	2010-5-24 17:53
アドミッタンスパラメータと４端子定数	webadm	2010-5-26 11:41
伝送行列	webadm	2010-5-26 14:34
T形回路の伝送行列	webadm	2010-5-26 15:14
4端子定数	webadm	2010-5-27 3:18
続：伝送行列	webadm	2010-5-27 13:50
続：４端子定数	webadm	2010-5-27 22:14
続々：４端子定数	webadm	2010-5-29 3:39
インピーダンス行列	webadm	2010-5-29 11:27
アドミッタンス行列	webadm	2010-5-29 11:57
またまた：４端子定数	webadm	2010-5-30 11:15
二端子対回路の並列接続	webadm	2010-5-30 12:37
もうひとつの：４端子定数	webadm	2010-5-30 12:45
アドミッタンスパラメータ	webadm	2010-6-3 12:42
まだまだ：４端子定数	webadm	2010-6-5 13:04
影像パラメータと４端子定数	webadm	2010-6-5 13:44
影像パラメータ	webadm	2010-6-12 22:30
続：影像パラメータ	webadm	2010-6-13 5:07
続々：影像パラメータ	webadm	2010-6-17 5:13
影像インピーダンス	webadm	2010-6-17 16:21
続：影像インピーダンス	webadm	2010-6-17 19:40
まだまだ：影像パラメータ	webadm	2010-6-22 18:50
もうひとつの：影像パラメータ	webadm	2010-6-25 21:54
４端子定数と影像インピーダンス	webadm	2010-6-26 0:45
インピーダンス整合	webadm	2010-6-26 11:27
もうひとつの：影像インピーダンス	webadm	2010-6-26 21:55
反復インピーダンスと４端子定数	webadm	2010-6-27 0:05
反復パラメータ	webadm	2010-6-28 21:04
影像インピーダンスと反復インピーダンス	webadm	2010-6-29 18:16
π形回路の伝送行列、影像パラメータ、反復パラメータ	webadm	2010-7-8 21:06
相互誘導回路と理想変成器	webadm	2010-7-28 6:11
Norton変換	webadm	2010-8-17 10:44
続：Norton変換	webadm	2010-8-17 20:48
容量性変成器	webadm	2010-8-18 3:42
抵抗性変成器	webadm	2010-8-21 10:11
理想ジャイレーター	webadm	2010-10-31 3:26
続：理想ジャイレータ	webadm	2010-11-19 2:41
続々：ジャイレータ	webadm	2010-11-23 21:29
対称回路	webadm	2010-11-25 9:18
続：対称回路	webadm	2010-11-30 0:01
続々：対称回路	webadm	2010-11-30 9:27
またまた：対称回路	webadm	2010-11-30 23:28
軸対称二端子対回路	webadm	2010-12-3 8:26
一方向性回路	webadm	2010-12-8 9:13
続：一方向性回路	webadm	2010-12-8 10:37
Zパラメータ	webadm	2010-12-9 22:51
続：Zパラメータ	webadm	2010-12-10 0:17
４端子定数	webadm	2010-12-14 6:51
理想オペアンプ	webadm	2010-12-14 7:03
続々：Zパラメータ	webadm	2010-12-20 10:10
reactance回路	webadm	2010-12-20 22:52
全域通過回路	webadm	2010-12-23 13:53
最小位相推移回路	webadm	2010-12-23 21:54
続：最小位相推移回路	webadm	2011-4-22 7:02
» 続々：最小位相推移回路	webadm	2011-4-22 9:38

投稿するにはまず登録を