Gan's blog - フォーラム

« 1 (2) 3 4 5 ... 7 »

投稿者	スレッド
webadm	投稿日時: 2010-5-26 11:41
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3091	アドミッタンスパラメータと４端子定数次ぎはアドミッタンスパラメータと４端子定数の間の変換式を導く問題。アドミッタンスパラメータ（Y行列）とはなにか思い出すと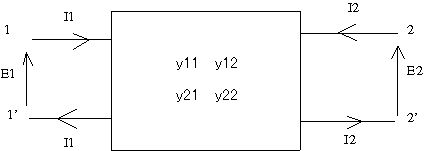上記の回路で $\begin{eqnarray}<br />\left[\begin{array}<br />I_1\\<br />I_2<br />\end{array}\right]&=&\left[\begin{array}<br />y_{11} & y_{12}\\<br />y_{21} & y_{22}<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]\\<br />y_{11}&=&\left.\frac{I_1}{E_1}\right\|_{E_2=0}\\<br />y_{12}&=&\left.\frac{I_1}{E_2}\right\|_{E_1=0}\\<br />y_{21}&=&\left.\frac{I_2}{E_1}\right\|_{E_2=0}\\<br />y_{22}&=&\left.\frac{I_2}{E_2}\right\|_{E_1=0}<br />\end{eqnarray}$ が成り立つことを表す。一方で４端子対定数(F行列）は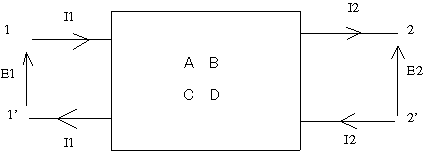上記の回路で $\begin{eqnarray}<br />\left[\begin{array}<br />E_1\\<br />I_1<br />\end{array}\right]&=&\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />I_2<br />\end{array}\right]\\<br />A&=&\left.\frac{E_1}{E_2}\right\|_{I_2=0}\\<br />B&=&\left.\frac{E_1}{I_2}\right\|_{E_2=0}\\<br />C&=&\left.\frac{I_1}{E_2}\right\|_{I_2=0}\\<br />D&=&\left.\frac{I_1}{I_2}\right\|_{E_2=0}<br />\end{eqnarray}$ が成り立つことを意味する。２つの回路ではI2の向きが逆なので注意しながらYパラメータの条件(E2=0,E1=0)をF行列表現の式に適用すると $\begin{eqnarray}<br />\left[\begin{array}<br />E_1\\<br />I_1<br />\end{array}\right]&=&\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]\left[\begin{array}<br />0\\<br />-I_2<br />\end{array}\right]\\<br />E_1&=&\left.-B I_2\right\|_{E_2=0}\\<br />I_1&=&\left.-D I_2\right\|_{E_2=0}\\<br />\left[\begin{array}<br />0\\<br />I_1<br />\end{array}\right]&=&\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />-I_2<br />\end{array}\right]\\<br />0&=&\left.A E_2-B I_2\right\|_{E_1=0}\\<br />I_1&=&\left.A E_2-D I_2\right\|_{E_1=0}<br />\end{eqnarray}$ これらの関係からYパラメータは $\begin{eqnarray}<br />y_{11}&=&\left.\frac{I_1}{E_1}\right\|_{E_2=0}\\<br />&=&\left.\frac{-D I_2}{-B I_2}\right\|_{E_2=0}\\<br />&=&\frac{D}{B}\\<br />y_{12}&=&\left.\frac{I_1}{E_2}\right\|_{E_1=0}\\<br />&=&\left.\frac{C E_2-D I_2}{\frac{B}{A}I_2}\right\|_{E_1=0}\\<br />&=&\left.\frac{\frac{C B}{A}I_2-D I_2}{\frac{B}{A}I_2}\right\|_{E_1=0}\\<br />&=&\frac{C B - A D}{B}\\<br />&=&-\frac{A D- B C}{B}<br />y_{21}&=&\left.\frac{I_2}{E_1}\right\|_{E_2=0}\\<br />&=&\left.\frac{-\frac{E_1}{B}}{E_1}\right\|_{E_2=0}\\<br />&=&-\frac{1}{B}\\<br />y_{22}&=&\left.\frac{I_2}{E_2}\right\|_{E_1=0}\\<br />&=&\left.\frac{\frac{A}{B}E_2}{E_2}\right\|_{E_1=0}\\<br />&=&\frac{A}{B}\\<br />\left[\begin{array}<br />y_{11} & y_{12}\\<br />y_{21} & y_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />\frac{D}{B} & -\frac{A D- B C}{B}\\<br />-\frac{1}{B} & \frac{A}{B}<br />\end{array}\right]<br />\end{eqnarray}$ とFパラメータ要素で表される。同様にFパラメータの条件でFパラメータをYパラメータで書き直しても良いが、上記の関係式をFパラメータに付いて解くと $\begin{eqnarray}<br />A&=&-\frac{y_{22}}{y_{21}}\\<br />B&=&-\frac{1}{y_{21}}\\<br />C&=&-\frac{y_{11}y_{22}}{y_{21}}+\frac{y_{12}}{y_{21}}\\<br />&=&\frac{y_{12}y_{21}-y_{11}y_{22}}{y_{21}}\\<br />&=&-\frac{y_{11}y_{22}-y_{12}y_{21}}{y_{21}}\\<br />D&=&-\frac{y_{11}}{y_{21}}\\<br />\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]&=&\left[\begin{array}<br />-\frac{y_{22}}{y_{21}} & -\frac{1}{y_{21}}\\<br />-\frac{y_{11}y_{22}-y_{12}y_{21}}{y_{21}} & -\frac{y_{11}}{y_{21}}<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。 P.S 最初同じ要領でFパラメータをYパラメータで表すことを試みたらどうも結果がおかしいので、先に導いたYパラメータをFパラメータで表した関係から逆に導いたのだが、よく見たら理論の時のFパラメータ条件をI2=0ではなくI1=0と誤記していたのが原因だった。それで矛盾が生じたというわけである。なのでFパラメータの条件(I2=0とE2=0)をYパラメータの回路に当てはめてI2の極性に注意すれば同じ結果が得られるはずである。あと、線形代数をうまく使って同じ結果が得られると思うのだが、これも読者の課題としよう(´∀` ) P.S 後の問題でここの解を利用したらおかしな結果にしかならないので、良くみたら式の途中で痛恨の転記ミス発見(;´Д`) (2010/05/30) Y-F変換の導出過程でCの最初の式に転記ミスがあったのを今更修正 2012/11/4)

webadm	投稿日時: 2010-5-26 14:34
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3091	伝送行列次ぎは伝送行列の問題。以下の基本回路に対する伝送行列を求めよというもの。伝送行列(F行列）の定義を再掲すると $\begin{eqnarray}<br />\left[\begin{array}<br />E_1\\<br />I_1<br />\end{array}\right]&=&\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />I_2<br />\end{array}\right]\\<br />A&=&\left.\frac{E_1}{E_2}\right\|_{I_2=0}\\<br />B&=&\left.\frac{E_1}{I_2}\right\|_{E_2=0}\\<br />C&=&\left.\frac{I_1}{E_2}\right\|_{I_2=0}\\<br />D&=&\left.\frac{I_1}{I_2}\right\|_{E_2=0}<br />\end{eqnarray}$ 上記のFパラメータ条件を題意の回路に適用すればよいわけである。最初の回路の場合端子対2を開放（I2=0）と短絡(E2=0)について調べると $\begin{eqnarray}<br />E_1&=&\left.E_2\right\|_{I_2=0}\\<br />I_1&=&\left.0\right\|_{I_2=0}\\<br />I_1&=&\left.\frac{E_1}{Z}\right\|_{E_2=0}\\<br />I_1&=&\left.I_2\right\|_{E_2=0}<br />\end{eqnarray}$ この関係をFパラメータの条件式に適用すると $\begin{eqnarray}<br />A&=&\left.\frac{E_1}{E_2}\right\|_{I_2=0}\\<br />&=&1\\<br />B&=&\left.\frac{E_1}{I_2}\right\|_{E_2=0}\\<br />&=&\frac{Z I_1}{I_1}\\<br />&=&Z\\<br />C&=&\left.\frac{I_1}{E_2}\right\|_{I_2=0}\\<br />&=&\left.\frac{0}{E_2}\right\|_{I_2=0}\\<br />&=&0\\<br />D&=&\left.\frac{I_1}{I_2}\right\|_{E_2=0}\\<br />&=&1\\<br />\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]&=&\left[\begin{array}<br />1 & Z\\<br />0 & 1<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。二番目の回路の場合端子対2を開放（I2=0）と短絡(E2=0)について調べると $\begin{eqnarray}<br />E_1&=&\left.E_2\right\|_{I_2=0}\\<br />I_1&=&\left.\frac{E_1}{Z}\right\|_{I_2=0}\\<br />E_1&=&\left.0\right\|_{E_2=0}\\<br />I_1&=&\left.I_2\right\|_{E_2=0}<br />\end{eqnarray}$ この関係をFパラメータの条件式に適用すると $\begin{eqnarray}<br />A&=&\left.\frac{E_1}{E_2}\right\|_{I_2=0}\\<br />&=&1\\<br />B&=&\left.\frac{E_1}{I_2}\right\|_{E_2=0}\\<br />&=&\frac{0}{I_2}\\<br />&=&0\\<br />C&=&\left.\frac{I_1}{E_2}\right\|_{I_2=0}\\<br />&=&\left.\frac{\frac{E_1}{Z}}{E_1}\right\|_{I_2=0}\\<br />&=&\frac{1}{Z}\\<br />D&=&\left.\frac{I_1}{I_2}\right\|_{E_2=0}\\<br />&=&1\\<br />\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]&=&\left[\begin{array}<br />1 & 0\\<br />\frac{1}{Z} & 1<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。

webadm	投稿日時: 2010-5-26 15:14
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3091	T形回路の伝送行列次ぎも伝送行列の問題。 T形回路の伝送行列を導いて、AD-BC=1であること対称回路ではA=Dが成り立つことを確認し、与えられた回路の伝送行列を求めよというもの。前問と同様にFパラメータ条件(出力端開放:I2=0,出力端短絡：E2=0)で解析すると $\begin{eqnarray}<br />E_2&=&\left.Z_2 I_1\right\|_{I_2=0}\\<br />I_1&=&\left.\frac{E_1}{Z_1+Z_2}\right\|_{I_2=0}\\<br />I_2&=&\left.\frac{\frac{E_1 Z_2}{Z_1+Z_2}}{\frac{Z_1 Z_2}{Z_1+Z_2}+Z_3}\right\|_{E_2=0}\\<br />I_1&=&\left.\frac{E_1}{Z_1+\frac{Z_2 Z_3}{Z_2+Z_3}}\right\|_{E_2=0}<br />\end{eqnarray}$ 従ってFパラメータは $\begin{eqnarray}<br />A&=&\left.\frac{E_1}{E_2}\right\|_{I_2=0}\\<br />&=&\left.\frac{\cancel{I_1}\left(Z_1+Z_2\right)}{Z_2 \cancel{I_1}}\right\|_{I_2=0}\\<br />&=&\frac{Z_1+Z_2}{Z_2}\\<br />&=&1+\frac{Z_1}{Z_2}\\<br />B&=&\left.\frac{E_1}{I_2}\right\|_{E_2=0}\\<br />&=&\left.\frac{\frac{\cancel{I_2}\left(\frac{Z_1 Z_2}{Z_1+Z_2}+Z_3\right)}{\frac{Z_2}{Z_1+Z_2}}}{\cancel{I_2}}\right\|_{E_2=0}\\<br />&=&\frac{\frac{Z_1 Z_2}{Z_1+Z_2}+Z_3}{\frac{Z_2}{Z_1+Z_2}}\\<br />&=&\frac{Z_1 Z_2+Z_1 Z_3+Z_2 Z_3}{Z_2}\\<br />C&=&\left.\frac{I_1}{E_2}\right\|_{I_2=0}\\<br />&=&\left.\frac{\cancel{I_1}}{Z_2 \cancel{I_1}}\right\|_{I_2=0}\\<br />&=&\frac{1}{Z_2}\\<br />D&=&\left.\frac{I_1}{I_2}\right\|_{E_2=0}\\<br />&=&\left.\frac{\frac{\cancel{E_1}}{Z_1+\frac{Z_2 Z_3}{Z_2+Z_3}}}{\frac{\frac{\cancel{E_1} Z_2}{Z_1+Z_2}}{\frac{Z_1 Z_2}{Z_1+Z_2}+Z_3}}\right\|_{E_2=0}\\<br />&=&\frac{\frac{\frac{Z_1 Z_2}{Z_1+Z_2}+Z_3}{Z_1+\frac{Z_2 Z_3}{Z_2+Z_3}}}{\frac{Z_2}{Z_1+Z_2}}\\<br />&=&\frac{\frac{\frac{\cancel{Z_1 Z_2+Z_1 Z_3+Z_2 Z_3}}{\cancel{Z_1+Z_2}}}{\frac{\cancel{Z_1 Z_2+Z_1 Z_3+Z_2 Z_3}}{Z_2+Z_3}}}{\frac{Z_2}{\cancel{Z_1+Z_2}}}\\<br />&=&\frac{Z_2+Z_3}{Z_2}\\<br />&=&1+\frac{Z_3}{Z_2}\\<br />\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]&=&\left[\begin{array}<br />1+\frac{Z_1}{Z_2} & \frac{Z_1 Z_2+Z_1 Z_3+Z_2 Z_3}{Z_2}\\<br />\frac{1}{Z_2} & 1+\frac{Z_3}{Z_2}<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。従ってAD-BCは $\begin{eqnarray}<br />A D - B C&=&\left(1+\frac{Z_1}{Z_2}\right)\left(1+\frac{Z_3}{Z_2}\right)-\left(\frac{Z_1 Z_2+Z_1 Z_3+Z_2 Z_3}{Z_2}\right)\left(\frac{1}{Z_2}\right)\\<br />&=&\left(\frac{Z_1+Z_2}{Z_2}\right)\left(\frac{Z_2+Z_3}{Z_2}\right)-\frac{Z_1 Z_2+Z_1 Z_3+Z_2 Z_3}{{Z_2}^2}\\<br />&=&\frac{Z_1 Z_2+Z_1 Z_3+Z_2 Z_3+{Z_2}^2}{{Z_2}^2}-\frac{Z_1 Z_2+Z_1 Z_3+Z_2 Z_3}{{Z_2}^2}\\<br />&=&1<br />\end{eqnarray}$ ということになる。また対称回路ではZ1=Z3となることから $\begin{eqnarray}<br />A&=&1+\frac{Z_1}{Z_2}\\<br />&=&1+\frac{Z_3}{Z_2}\\<br />&=&D<br />\end{eqnarray}$ ということになる。以下の回路について伝送行列を求めると $\begin{eqnarray}<br />Z_1&=&R\\<br />Z_2&=&j\omega L\\<br />Z_3&=&-\frac{j}{\omega C}<br />\end{eqnarray}$ を先のF行列に代入すると $\begin{eqnarray}<br />A&=&1+\frac{Z_1}{Z_2}\\<br />&=&\1+\frac{R}{j\omega L}\\<br />&=&1-j\frac{R}{\omega L}\\<br />B&=&\frac{Z_1 Z_2+Z_1 Z_3+Z_2 Z_3}{Z_2}\\<br />&=&\frac{j\omega L R-\frac{j R}{\omega C}+\frac{\omega L}{\omega C}}{j\omega L}\\<br />&=&\frac{R\left(\omega L\right-\frac{1}{\omega C})-j\frac{L}{C}}{\omega L}\\<br />&=&R\left(1-\frac{1}{{\omega}^2 L C}\right)-j\frac{L}{\omega C}\\<br />C&=&\frac{1}{Z_2}\\<br />&=&\frac{1}{j\omega L}\\<br />D&=&1+\frac{Z_3}{Z_2}\\<br />&=&1-\frac{\frac{j}{\omega C}}{j\omega L}\\<br />&=&1-\frac{1}{{\omega}^2 L C}\\<br />\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]&=&\left[\begin{array}<br />1-j\frac{R}{\omega L} & R\left(1-\frac{1}{{\omega}^2 L C}\right)-j\frac{L}{\omega C}\\<br />\frac{1}{j\omega L} & 1-\frac{1}{{\omega}^2 L C}<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。同様に次ぎの回路も $\begin{eqnarray}<br />Z_1&=&j\omega L\\<br />Z_2&=&\frac{1}{j\omega C}\\<br />Z_3&=&j\omega L<br />\end{eqnarray}$ を先のF行列に代入すると $\begin{eqnarray}<br />A&=&1+\frac{Z_1}{Z_2}\\<br />&=&\1-\frac{j\omega L}{\frac{j}{\omega C}}\\<br />&=&1-{\omega}^2 L C\\<br />B&=&\frac{Z_1 Z_2+Z_1 Z_3+Z_2 Z_3}{Z_2}\\<br />&=&\frac{j\omega L \frac{1}{j\omega C}+j\omega L j\omega L+\frac{1}{j\omega C} j\omega L}{\frac{1}{j\omega C}}\\<br />&=&j\omega C\left(\frac{L}{C}-{\omega}^2 L^2+\frac{L}{C}\right)\\<br />&=&j\omega L\left(2-{\omega}^2L C\right)\\<br />C&=&\frac{1}{Z_2}\\<br />&=&\frac{1}{\frac{1}{j\omega C}}\\<br />&=&j\omega C\\<br />D&=&1+\frac{Z_3}{Z_2}\\<br />&=&1+\frac{j\omega L}{\frac{1}{j\omega C}}\\<br />&=&1-{\omega}^2 L C\\<br />\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]&=&\left[\begin{array}<br />1-{\omega}^2 L C & j\omega L\left(2-{\omega}^2L C\right)\\<br />j\omega C & 1-{\omega}^2 L C<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。

webadm	投稿日時: 2010-5-27 3:18
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3091	4端子定数次ぎも４端子定数に関する問題。題意はFパラメータ条件（出力開放：I2=0,出力短絡:E2=0)における未知の回路の解析結果を元に４端子定数を求めよというもの。既に何度も出てきたFパラメータの定義を知っていればなんのことは無い。題意では $\begin{eqnarray}<br />E_1&=&\left.10\right\|_{I_2=0}\\<br />I_1&=&\left.0.5\right\|_{I_2=0}\\<br />E_2&=&\left.4\right\|_{I_2=0}\\<br />E_1&=&\left.10\right\|_{E_2=0}\\<br />I_2&=&\left.0.2\right\|_{E_2=0}<br />\end{eqnarray}$ 従って４端子定数は $\begin{eqnarray}<br />A&=&\left.\frac{E_1}{E_2}\right\|_{I_2=0}\\<br />&=&\left.\frac{10}{4}\right\|_{I_2=0}\\<br />&=&2.5\\<br />B&=&\left.\frac{E_1}{I_2}\right\|_{E_2=0}\\<br />&=&\left.\frac{10}{0.2}\right\|_{E_2=0}\\<br />&=&50\\<br />C&=&\left.\frac{I_1}{E_2}\right\|_{I_2=0}\\<br />&=&\left.\frac{0.5}{4}\right\|_{I_2=0}\\<br />&=&0.125\\<br />D&=&\left.\frac{I_1}{I_2}\right\|_{E_2=0}\\<br />&=&\frac{1+B C}{A}\\<br />&=&\frac{1+50\times 0.125}{2.5}\\<br />&=&2.9\\<br />\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]&=&\left[\begin{array}<br />5 & 50\\<br />0.125 & 2.9<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。題意ではE2=0の条件でのI1が与えられていないので、直接パラメータDを求めることができないが、線形回路ではAD-BC=1が成り立つので、既に得られているA,B,CからDを割り出すというのがこの問題のミソ。（続く）

webadm	投稿日時: 2010-5-27 13:50
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3091	続：伝送行列次ぎも伝送行列の問題。伝送行列と呼んだり４端子定数と呼んだり統一されていないのは、オリジナルの問題文が異なる著書から引用しているからだろうか。以下の回路の伝送行列を求めよというもの。ただしG=1/Rとする。いろいろやり方はあるが著者とは違う方法で伝送行列は小さな二端子対回路の縦続接続で考えると楽なのでその点では共通である。既に以前の問題で出てきたT形回路を含む以下の基本回路の縦続接続として考える。左から順番に各基本回路の伝送行列は前出の問題の解より $\begin{eqnarray}<br />\left[F_1\right]&=&\left[\begin{array}<br />1+R G & \left(\frac{R}{G}+\frac{R}{G}+R R\right)G\\<br />G & 1+R G<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />1+R G & R\left(2+R G\right)\\<br />G & 1+R G<br />\end{array}\right]\\<br />\left[F_2\right]&=&\left[\begin{array}<br />1 & 0\\<br />G & 1<br />\end{array}\right]\\<br />\left[F_3\right]&=&\left[\begin{array}<br />1 & R\\<br />0 & 1<br />\end{array}\right]<br />\end{eqnarray}$ ということになり、従って全体の回路の伝送行列は $\begin{eqnarray}<br />\left[F\right]&=&\left[F_1\right]\left[F_2\right]\left[F_3\right]\\<br />&=&\left[\begin{array}<br />1+R G & R\left(2+R G\right)\\<br />G & 1+R G<br />\end{array}\right]\left[\begin{array}<br />1 & 0\\<br />G & 1<br />\end{array}\right]\left[\begin{array}<br />1 & R\\<br />0 & 1<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />1+R G & R\left(2+R G\right)\\<br />G & 1+R G<br />\end{array}\right]\left[\begin{array}<br />1 & R\\<br />G & G R+1<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />G R \left( G R+2\right) +G R+1 & R \left( G R+1\right) \left( G R+2\right) +R \left( G R+1\right) \\<br />G \left( G R+1\right) +G & {\left( G R+1\right) }^{2}+G R<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />{G}^{2} {R}^{2}+3 G\,R+1 & R \left( G R+1\right) \left( G R+3\right) \\<br />G \left( G R+2\right) & {G}^{2} {R}^{2}+3 G R+1<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />1+3+1 & R \left(1+1\right) \left( 1+3\right) \\<br />\frac{1}{R}\left( 1+2\right) & 1+3+1<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />5 & 8 R\\<br />\frac{3}{R} & 5<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。 P.S 最初どうも著者の答えと合わないと思ったら、途中の回路のF行列の内容を間違えていた...orz ひっかけではないが並列接続の抵抗がRではなくGと表記されているのは、後に学ぶ分布定数回路とかでの慣例であるため。でもひっかけかな。そのまま記号として既知の式を置き換えるわけにはいかない。あくまで逆数表記だと意識する必要がある。

webadm	投稿日時: 2010-5-27 22:14
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3091	続：４端子定数次ぎも４端子定数の問題。端子対22'を開放及び短絡時の端子対11'から見たインピーダンスをそれぞれZ1f,Z1sとし、端子対11'を短絡したとき端子対22'から見たインピーダンスをZ2sとした場合の４端子定数を求めよというもの。題意で与えられた条件はインピーダンスパラメータやアドミッタンスパラメータそのものである $\begin{eqnarray}<br />Z_{1f}&=&\left.\frac{E_1}{I_1}\right\|_{I_2=0}=Z_{11}\\<br />Z_{1s}&=&\left.\frac{E_1}{I_1}\right\|_{E_2=0}=\frac{1}{Y_{11}}\\<br />Z_{2s}&=&\left.\frac{E_2}{I_2}\right\|_{E_1=0}=\frac{1}{Y_{22}}<br />\end{eqnarray}$ ただしZパラメータやYパラメータから４端子定数を導けという問題ではなく、上の３つのパラメータだけで表せということになる。それははたして可能だろうか？相反定理が成り立つ線形受動回路では以下が成り立つので３つの独立パラメータだけで必要十分ということになる。 $\begin{eqnarray}<br />Z_{12}&=&Z_{21}\\<br />Y_{12}&=&Y_{21}\\<br />A D - B C&=&1<br />\end{eqnarray}$ ストラテジーとして以前Hパラメータ変換問題でやったように線形代数を駆使して求めてみよう。４端子定数はベクトルP(E2,I2')をQ(E1,I1)へ変換する。一方等価な回路のZパラメータやYパラメータはP'(E1,E2),Q'(I1,I2)の間の線形変換行列である。それぞれの数ベクトルP,Q,P',Q'の間には以下の関係が成り立つとする。ただしI2'=-I2。 $\begin{eqnarray}<br />P&=&\left[\begin{array}<br />E_2\\<br />I^{\'}_2<br />\end{array}\right]=\left[\begin{array}<br />0 & 1\\<br />0 & 0<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]+\left[\begin{array}<br />0 & 0\\<br />0 & -1<br />\end{array}\right]\left[\begin{array}<br />I_1\\<br />I_2<br />\end{array}\right]=\left[\begin{array}<br />0 & 1\\<br />0 & 0<br />\end{array}\right]P^{\'}+\left[\begin{array}<br />0 & 0\\<br />0 & -1<br />\end{array}\right]Q^{\'}\\<br />Q&=&\left[\begin{array}<br />E_1\\<br />I_1<br />\end{array}\right]=\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]+\left[\begin{array}<br />0 & 0\\<br />1 & 0<br />\end{array}\right]\left[\begin{array}<br />I_1\\<br />I_2<br />\end{array}\right]=\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]P^{\'}+\left[\begin{array}<br />0 & 0\\<br />1 & 0<br />\end{array}\right]Q^{\'}<br />\end{eqnarray}$ 従って４端子定数とP,Qの関係は $\begin{eqnarray}<br />Q=F P=\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]P=\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]\left(\left[\begin{array}<br />0 & 1\\<br />0 & 0<br />\end{array}\right]P^{\'}+\left[\begin{array}<br />0 & 0\\<br />0 & -1<br />\end{array}\right]Q^{\'}\right)&=&\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]P^{\'}+\left[\begin{array}<br />0 & 0\\<br />1 & 0<br />\end{array}\right]Q^{\'}\\<br />\left(\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]\left[\begin{array}<br />0 & 1\\<br />0 & 0<br />\end{array}\right]-\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]\right)P^{\'}&=&\left(\left[\begin{array}<br />0 & 0\\<br />1 & 0<br />\end{array}\right]-\left(\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]\left[\begin{array}<br />0 & 0\\<br />0 & -1<br />\end{array}\right]\right)Q^{\'}\\<br />\left[\begin{array}<br />-1 & A\\<br />0 & C<br />\end{array}\right]P^{\'}&=&\left[\begin{array}<br />0 & B\\<br />1 & D<br />\end{array}\right]Q^{\'}<br />\end{eqnarray}$ 左辺の係数行列の逆行列を両辺に乗じると $\begin{eqnarray}<br />P^{\'}&=&\left[\begin{array}<br />-1 & A\\<br />0 & C<br />\end{array}\right]^{-1}\left[\begin{array}<br />0 & B\\<br />1 & D<br />\end{array}\right]Q^{\'}\\<br />&=&\left[\begin{array}<br />-1 & \frac{A}{C}\\<br />0 & \frac{1}{C}<br />\end{array}\right]\left[\begin{array}<br />0 & B\\<br />1 & D<br />\end{array}\right]Q^{\'}\\<br />&=&\left[\begin{array}<br />\frac{A}{C} & \frac{A D}{C}-B\\<br />\frac{1}{C} & \frac{D}{C}<br />\end{array}\right]Q^{\'}\\<br />&=&\left[\begin{array}<br />\frac{A}{C} & \frac{A D-B C}{C}\\<br />\frac{1}{C} & \frac{D}{C}<br />\end{array}\right]Q^{\'}\\<br />&=&\left[\begin{array}<br />Z_{11} & Z_{12}\\<br />Z_{21} & Z_{22}<br />\end{array}\right]Q^{\'}<br />\end{eqnarray}$ 従って等価なF行列とZ行列の関係は $\begin{eqnarray}<br />\left[\begin{array}<br />Z_{11} & Z_{12}\\<br />Z_{21} & Z_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />\frac{A}{C} & \frac{A D-B C}{C}\\<br />\frac{1}{C} & \frac{D}{C}<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。同様にF行列と等価なY行列を求めるには上の式にZ行列の逆行列を求めればよく $\begin{eqnarray}<br />\left[\begin{array}<br />Y_{11} & Y_{12}\\<br />Y_{21} & Y_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />Z_{11} & Z_{12}\\<br />Z_{21} & Z_{22}<br />\end{array}\right]^{-1}=\left[\begin{array}<br />\frac{A}{C} & \frac{A D-B C}{C}\\<br />\frac{1}{C} & \frac{D}{C}<br />\end{array}\right]^{-1}\\<br />&=&\left[\begin{array}<br />\frac{D}{C \left( \frac{A D}{{C}^{2}}-\frac{A D-B C}{{C}^{2}}\right) } & -\frac{A D-B C}{C \left( \frac{A D}{{C}^{2}}-\frac{A D-B C}{{C}^{2}}\right) }\\<br />-\frac{1}{C \left( \frac{A D}{{C}^{2}}-\frac{A D-B C}{{C}^{2}}\right) } & \frac{A}{C \left( \frac{A D}{{C}^{2}}-\frac{A D-B C}{{C}^{2}}\right) }<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />\frac{D}{B} & -\frac{A D-B C}{B}\\<br />-\frac{1}{B} & \frac{A}{B}<br />\end{array}\right]<br />\end{eqnarray}$ 従って題意より $begin{eqnarray}<br />Z_{1f}&=&\left.\frac{E_1}{I_1}\right\|_{I_2=0}=Z_{11}\\<br />&=&\frac{A}{C}\\<br />Z_{1s}&=&\left.\frac{E_1}{I_1}\right\|_{E_2=0}=\frac{1}{Y_{11}}\\<br />&=&\frac{B}{D}\\<br />Z_{2s}&=&\left.\frac{E_2}{I_2}\right\|_{E_1=0}=\frac{1}{Y_{22}}\\<br />&=&\frac{B}{A}\\<br />A D - B C &=& 1<br />\end{eqnarray}$ という関係が成り立ち。上記をA,B,C,Dに関する連立方程式としてMaximaで解くと $\begin{eqnarray}<br />A&=&\sqrt{\frac{Z1f Z1s}{ Z2s\left(Z1f-Z1s\right)}}\\<br />B&=&\sqrt{\frac{Z1f Z1s Z2s}{Z1f-Z1s}}\\<br />C&=&\sqrt{\frac{Z1s}{Z1f Z2s\left(Z1f-Z1s\right)}}\\<br />D&=&\sqrt{\frac{Z1f Z2s}{Z1s\left(Z1f- Z1s\right)}}<br />\end{eqnarray}$ ということになる。最後だけ線形代数というわけにはいかなくなってしまった。実は良いところまでいったのだけれども、最後まで詰められなかった。更に磨きをかけるのは読者の課題としよう(´∀` ) P.S 最後のところは二次形式を使えば行列で扱えそうな気がするが。結局Maximaで解くという落ちになってしまった。Maxima自身もこの手の方程式を解くには苦手なのだが今回はあっさり解いてくれた。どうやってやってるのだろうか。

webadm	投稿日時: 2010-5-29 3:39
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3091	続々：４端子定数次ぎも４端子定数の問題。前問と違って今度は駆動点インピーダンスの代わりに、片方の端子対を短絡した状態で他方に与えられた電圧を加えた場合のそれぞれの端子対に流れる複素電流値から４端子定数を求めよという計算問題。図で表すと４つの不定元(A,B,C,D)を与えられた複素係数(二組のE1,E2,I1,I2）から求めれば良いので、前問の様に連立方程式を解けば簡単だが、別解を考えてみよう。基本的に連立方程式を解く点は代わらないが少し見通しを良くしよう。４端子定数,A,B,C,Dを不定元とすると $\begin{eqnarray}<br />\left[\begin{array}<br />E^{\'}_2 & -I^{\'}_2 & 0 & 0\\<br />E^{\'\'}_2 & -I^{\'\'}_2 & 0 & 0\\<br />0 & 0 & E^{\'}_2 & -I^{\'}_2\\<br />0 & 0 & E^{\'\'}_2 & -I^{\'\'}_2<br />\end{array}\right]\left[\begin{array}<br />A\\<br />B\\<br />C\\<br />D<br />\end{array}\right]&=&\left[\begin{array}<br />E^{\'}_1\\<br />E^{\'\'}_1\\<br />I^{\'}_1\\<br />I^{\'\'}_1<br />\end{array}\right]\\<br />\left[\begin{array}<br />A\\<br />B\\<br />C\\<br />D<br />\end{array}\right]&=&\left[\begin{array}<br />E^{\'}_2 & -I^{\'}_2 & 0 & 0\\<br />E^{\'\'}_2 & -I^{\'\'}_2 & 0 & 0\\<br />0 & 0 & E^{\'}_2 & -I^{\'}_2\\<br />0 & 0 & E^{\'\'}_2 & -I^{\'\'}_2<br />\end{array}\right]^{-1}\left[\begin{array}<br />E^{\'}_1\\<br />E^{\'\'}_1\\<br />I^{\'}_1\\<br />I^{\'\'}_1<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />\frac{I^{\'\'}_2}{E^{\'}_2 I^{\'\'}_2-E^{\'\'}_2 I^{\'}_2} & -\frac{I^{\'}_2}{E^{\'}_2 I^{\'\'}_2-E^{\'\'}_2 I^{\'}_2} & 0 & 0\\<br />\frac{E^{\'\'}_2}{E^{\'}_2 I^{\'\'}_2-E^{\'\'}_2 I^{\'}_2} & -\frac{E^{\'}_2}{E^{\'}_2 I^{\'\'}_2-E^{\'\'}_2 I^{\'}_2} & 0 & 0\\<br />0 & 0 & \frac{I^{\'\'}_2}{E^{\'}_2 I^{\'\'}_2-E^{\'\'}_2 I^{\'}_2} & -\frac{I^{\'}_2}{E^{\'}_2 I^{\'\'}_2-E^{\'\'}_2 I^{\'}_2}\\<br />0 & 0 & \frac{E^{\'\'}_2}{E^{\'}_2 I^{\'\'}_2-E^{\'\'}_2 I^{\'}_2} & -\frac{E^{\'}_2}{E^{\'}_2 I^{\'\'}_2-E^{\'\'}_2 I^{\'}_2}<br />\end{array}\right]\left[\begin{array}<br />E^{\'}_1\\<br />E^{\'\'}_1\\<br />I^{\'}_1\\<br />I^{\'\'}_1<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />\frac{E^{\'}_1\,I^{\'\'}_2-E^{\'\'}_1\,I^{\'}_2}{E^{\'}_2\,I^{\'\'}_2-E^{\'\'}_2\,I^{\'}_2}\\<br />\frac{E^{\'}_1\,E^{\'\'}_2-E^{\'}_2\,E^{\'\'}_1}{E^{\'}_2\,I^{\'\'}_2-E^{\'\'}_2\,I^{\'}_2}\\<br />\frac{I^{\'}_1\,I^{\'\'}_2-I^{\'}_2\,I^{\'\'}_1}{E^{\'}_2\,I^{\'\'}_2-E^{\'\'}_2\,I^{\'}_2}\\<br />-\frac{E^{\'}_2\,I^{\'\'}_1-E^{\'\'}_2\,I^{\'}_1}{E^{\'}_2\,I^{\'\'}_2-E^{\'\'}_2\,I^{\'}_2}<br />\end{array}\right]<br />\end{eqnarray}$ と解ける。これに題意の電圧、電流値を代入すると $\begin{eqnarray}<br />\left[\begin{array}<br />A\\<br />B\\<br />C\\<br />D<br />\end{array}\right]&=&\left[\begin{array}<br />\frac{E^{\'}_1\,I^{\'\'}_2-E^{\'\'}_1\,I^{\'}_2}{E^{\'}_2\,I^{\'\'}_2-E^{\'\'}_2\,I^{\'}_2}\\<br />\frac{E^{\'}_1\,E^{\'\'}_2-E^{\'}_2\,E^{\'\'}_1}{E^{\'}_2\,I^{\'\'}_2-E^{\'\'}_2\,I^{\'}_2}\\<br />\frac{I^{\'}_1\,I^{\'\'}_2-I^{\'}_2\,I^{\'\'}_1}{E^{\'}_2\,I^{\'\'}_2-E^{\'\'}_2\,I^{\'}_2}\\<br />-\frac{E^{\'}_2\,I^{\'\'}_1-E^{\'\'}_2\,I^{\'}_1}{E^{\'}_2\,I^{\'\'}_2-E^{\'\'}_2\,I^{\'}_2}<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />1.0+j0.75\\<br />2.5\\<br />0.55+j1.3\\<br />2.0+j1.5<br />\end{array}\right]<br />\end{array}$ ということになる。見通しは良かったが計算が大変だった。全部Maximaでやったんだけどね。

webadm	投稿日時: 2010-5-29 11:27
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3091	インピーダンス行列次ぎは二端子対回路の接続に関する問題。以下の回路のインピーダンス行列を求めよというもの。インピーダンス行列が既知の二端子対回路の外側に端子対と直列にZ1とZ2がそれぞれ挿入された全体の回路のインピーダンス行列を求めることになる。著者はちょっと面倒なやり方をしているが、おそらく読者に最も簡単な答えを残しておいてあげているのだろう。そっちで解いてみよう。インピーダンス行列は複数の二端子対回路を直列に（端子対をシリーズに）接続するのに都合が良い。上の回路は以下のような２つの異なる二端子対回路を直列接続したものと考えることができる。上部の回路のインピーダンス行列は $\begin{eqnarray}<br />\left[\begin{array}<br />Z^{\'}_{11} & Z^{\'}_{12}\\<br />Z^{\'}_{21} & Z^{\'}_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />Z_1 & 0\\<br />0 & Z_2<br />\end{array}\right]<br />\end{eqnarray}$ 従って回路全体のインピーダンス行列は $\begin{array}<br />\left[\begin{array}<br />Z^{\'\'}_{11} & Z^{\'\'}_{12}\\<br />Z^{\'\'}_{21} & Z^{\'\'}_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />Z^{\'}_{11} & Z^{\'}_{12}\\<br />Z^{\'}_{21} & Z^{\'}_{22}<br />\end{array}\right]+\left[\begin{array}<br />Z_{11} & Z_{12}\\<br />Z_{21} & Z_{22}<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />Z_1 & 0\\<br />0 & Z_2<br />\end{array}\right]+\left[\begin{array}<br />Z_{11} & Z_{12}\\<br />Z_{21} & Z_{22}<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />Z_1+Z_{11} & Z_{12}\\<br />Z_{21} & Z_2+Z_{22}<br />\end{array}\right]<br />\end{array}$ ということになる。

webadm	投稿日時: 2010-5-29 11:57
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3091	アドミッタンス行列次ぎも似たような問題。今度は複数のアドミッタンス回路の並列接続に関するもの。以下の回路のアドミッタンス行列を求めよというもの。これは前の問題と良くにている。これもアドミッタンス行列を求める問題なのは、並列接続に都合が良いから。著者は簡単な解法を読者に残しておいているので、それを使わない手ははない。上の回路は以下のような２つの回路の並列接続だと見なすことができる。上部の回路のアドミッタンス行列は $\begin{eqnarray}<br />\left[\begin{array}<br />Y^{\'}_{11} & Y^{\'}_{12}\\<br />Y^{\'}_{21} & Y^{\'}_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />Y_1 & 0\\<br />0 & Y_2<br />\end{array}\right]<br />\end{eqnarray}$ 従って全体の回路のアドミッタンス行列は $\begin{eqnarray}<br />\left[\begin{array}<br />Y^{\'\'}_{11} & Y^{\'\'}_{12}\\<br />Y^{\'\'}_{21} & Y^{\'\'}_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />Y^{\'}_{11} & Y^{\'}_{12}\\<br />Y^{\'}_{21} & Y^{\'}_{22}<br />\end{array}\right]+\left[\begin{array}<br />Y_{11} & Y_{12}\\<br />Y_{21} & Y_{22}<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />Y_1 & 0\\<br />0 & Y_2<br />\end{array}\right]+\left[\begin{array}<br />Y_{11} & Y_{12}\\<br />Y_{21} & Y_{22}<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />Y_1+Y_{11} & Y_{12}\\<br />Y_{21} & Y_2+Y_{22}<br />\end{array}\right]\\<br />\end{eqnarray}$ ということになる。

webadm	投稿日時: 2010-5-30 11:15
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3091	またまた：４端子定数次ぎも４端子定数。以前の問題で見たような以下の回路の４端子定数を求めよというもの。著者は今回は最もストレートな方法で解いているので、それとは別解でやってみよう。 $\begin{eqnarray}<br />P&=&\left[\begin{array}<br />E_2\\<br />I^{\'}_2<br />\end{array}\right]=\left[\begin{array}<br />0 & 1\\<br />0 & 0<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]+\left[\begin{array}<br />0 & 0\\<br />0 & -1<br />\end{array}\right]\left[\begin{array}<br />I_1\\<br />I_2<br />\end{array}\right]=\left[\begin{array}<br />0 & 1\\<br />0 & 0<br />\end{array}\right]Q^{\'}+\left[\begin{array}<br />0 & 0\\<br />0 & -1<br />\end{array}\right]P^{\'}\\<br />Q&=&\left[\begin{array}<br />E_1\\<br />I_1<br />\end{array}\right]=\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />E_2<br />\end{array}\right]+\left[\begin{array}<br />0 & 0\\<br />1 & 0<br />\end{array}\right]\left[\begin{array}<br />I_1\\<br />I_2<br />\end{array}\right]=\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]Q^{\'}+\left[\begin{array}<br />0 & 0\\<br />1 & 0<br />\end{array}\right]P^{\'}<br />\end{eqnarray}$ $\begin{eqnarray}<br />Q^{\'}=Z P^{\'}&=&\left[\begin{array}<br />Z_{11} & Z_{12}\\<br />Z_{21} & Z_{22}<br />\end{array}\right]P^{\'}\\<br />\left[\begin{array}<br />0 & 0\\<br />1 & 0<br />\end{array}\right]P+\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]Q&=&\left[\begin{array}<br />Z_{11} & Z_{12}\\<br />Z_{21} & Z_{22}<br />\end{array}\right]\left(\left[\begin{array}<br />0 & 0\\<br />0 & -1<br />\end{array}\right]P+\left[\begin{array}<br />0 & 1\\<br />0 & 0<br />\end{array}\right]Q\right)\\<br />\left(\left[\begin{array}<br />Z_{11} & Z_{12}\\<br />Z_{21} & Z_{22}<br />\end{array}\right]\left[\begin{array}<br />0 & 1\\<br />0 & 0<br />\end{array}\right]-\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]\right)Q&=&\left(\left[\begin{array}<br />0 & 0\\<br />1 & 0<br />\end{array}\right]-\left(\left[\begin{array}<br />Z_{11} & Z_{12}\\<br />Z_{21} & Z_{22}<br />\end{array}\right]\left[\begin{array}<br />0 & 0\\<br />0 & -1<br />\end{array}\right]\right)P\\<br />\left[\begin{array}<br />-1 & Z_{11}\\<br />0 & Z_{21}<br />\end{array}\right]Q&=&\left[\begin{array}<br />0 & Z_{12}\\<br />1 & Z_{22}<br />\end{array}\right]P\\<br />Q&=&\left[\begin{array}<br />-1 & Z_{11}\\<br />0 & Z_{21}<br />\end{array}\right]^{-1}\left[\begin{array}<br />0 & Z_{12}\\<br />1 & Z_{22}<br />\end{array}\right]P\\<br />&=&\left[\begin{array}<br />-1 & \frac{Z_{11}}{Z_{21}}\\<br />0 & \frac{1}{Z_{21}}<br />\end{array}\right]\left[\begin{array}<br />0 & Z_{12}\\<br />1 & Z_{22}<br />\end{array}\right]P\\<br />&=&\left[\begin{array}<br />\frac{Z_{11}}{Z_{21}} & \frac{Z_{11} Z_{22}- Z_{12} Z_{21}}{Z21}\\<br />\frac{1}{Z_{21}} & \frac{Z_{22}}{Z_{21}}<br />\end{array}\right]P\\<br />&=&\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]P<br />\end{eqnarray}$ 以前の問題で同様の回路のインピーダンス行列を求めているので、それを４端子定数に変換すると $\begin{eqnarray}<br />Q^{\'}=Z P^{\'}&=&\left[\begin{array}<br />Z_s+Z_{11} & Z_{12}\\<br />Z_{21} & Z_r+Z_{22}<br />\end{array}\right]P^{\'}\\<br />\left[\begin{array}<br />0 & 0\\<br />1 & 0<br />\end{array}\right]P+\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]Q&=&\left[\begin{array}<br />Z_s+Z_{11} & Z_{12}\\<br />Z_{21} & Z_r+Z_{22}<br />\end{array}\right]\left(\left[\begin{array}<br />0 & 0\\<br />0 & -1<br />\end{array}\right]P+\left[\begin{array}<br />0 & 1\\<br />0 & 0<br />\end{array}\right]Q\right)\\<br />\left(\left[\begin{array}<br />Z_s+Z_{11} & Z_{12}\\<br />Z_{21} & Z_r+Z_{22}<br />\end{array}\right]\left[\begin{array}<br />0 & 1\\<br />0 & 0<br />\end{array}\right]-\left[\begin{array}<br />1 & 0\\<br />0 & 0<br />\end{array}\right]\right)Q&=&\left(\left[\begin{array}<br />0 & 0\\<br />1 & 0<br />\end{array}\right]-\left(\left[\begin{array}<br />Z_s+Z_{11} & Z_{12}\\<br />Z_{21} & Z_r+Z_{22}<br />\end{array}\right]\left[\begin{array}<br />0 & 0\\<br />0 & -1<br />\end{array}\right]\right)P\\<br />\left[\begin{array}<br />-1 & Z_{11}+Z_s\\<br />0 & Z_{21}<br />\end{array}\right]Q&=&\left[\begin{array}<br />0 & Z_{12}\\<br />1 & Z_{22}+Z_r<br />\end{array}\right]P\\<br />Q&=&\left[\begin{array}<br />-1 & Z_{11}+Z_s\\<br />0 & Z_{21}<br />\end{array}\right]^{-1}\left[\begin{array}<br />0 & Z_{12}\\<br />1 & Z_{22}+Z_r<br />\end{array}\right]P\\<br />&=&\left[\begin{array}<br />-1 & -\frac{-Z_{11}-Z_s}{Z_{21}}\\<br />0 & \frac{1}{Z_{21}}<br />\end{array}\right]\left[\begin{array}<br />0 & Z_{12}\\<br />1 & Z_{22}+Z_r<br />\end{array}\right]P\\<br />&=&\left[\begin{array}<br />\frac{Z_{11}+Z_s}{Z_{21}} & \frac{Z_{11} Z_{22}-Z_{12} Z_{21}}{Z_{21}}+Z_s \frac{Z_{22}}{Z_{21}}+Z_r\frac{Z_{11}}{Z_{21}}+\frac{Z_s Z_r}{Z_{21}}\\<br />\frac{1}{Z_{21}} & \frac{Z_{22}+Z_r}{Z_{21}}<br />\end{array}\right]P\\<br />&=&\left[\begin{array}<br />A^{\'} & B^{\'}\\<br />C^{\'} & D^{\'}<br />\end{array}\right]P<br />\end{eqnarray}$ 従って全体の回路の４端子定数は $\begin{eqnarray}<br />\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]&=&\left[\begin{array}<br />\frac{Z_{11}}{Z_{21}} & \frac{Z_{11} Z_{22}- Z_{12} Z_{21}}{Z21}\\<br />\frac{1}{Z_{21}} & \frac{Z_{22}}{Z_{21}}<br />\end{array}\right]\\<br />\left[\begin{array}<br />A^{\'} & B^{\'}\\<br />C^{\'} & D^{\'}<br />\end{array}\right]&=&\left[\begin{array}<br />\frac{Z_{11}+Z_s}{Z_{21}} & \frac{Z_{11} Z_{22}-Z_{12} Z_{21}}{Z_{21}}+Z_s \frac{Z_{22}}{Z_{21}}+Z_r\frac{Z_{11}}{Z_{21}}+\frac{Z_s Z_r}{Z_{21}}\\<br />\frac{1}{Z_{21}} & \frac{Z_{22}+Z_r}{Z_{21}}<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />A+Z_s C & B+Z_s D+Z_r A+Z_s Z_r C\\<br />C & D+Z_r C<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。 P.S 一部題意と異なる記号が使用されていた部分を訂正(2010/06/07)

« 1 (2) 3 4 5 ... 7 »

スレッド表示 | 新しいものから

前のトピック | 次のトピック | トップ

投稿するにはまず登録を