Gan's blog - フォーラム

メイン > > 電気回路理論おもちゃ箱 > 分布定数回路の定常現象演習問題

« 1 2 (3) 4 5 »

投稿者	スレッド
webadm	投稿日時: 2012-10-27 5:48
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	Ferranti効果次はFerranti効果に関する問題長距離送電線において、受電端を開放するとその点の電圧が送電端のそれよりも高くなることがあり、これをFerranti効果という。いま周波数f=60[Hz]の波が光速で伝搬するとき、送電線より5[%]電圧が高くなるのはこの電線の長さlがいくらのときか、ただし送電線は無損失であるとする。というもの。ストラテジーとしては (1) 送電端と受電端の電圧の関係式を導く (2) 受電端の電圧/送電端の電圧が1.05になる条件を見いだすがすぐに思いつく。まずは一般的な線路について導出して、それを題意の無損失線路のケースに特殊化する線路を二端子対回路とみなせば受電端の条件より以下の関係が成り立つ $\begin{eqnarray}<br />\begin{bmatrix}E_S\cr I_S\end{bmatrix}&=&\begin{bmatrix}\cosh\gamma\,l&Z_0\,\sinh\gamma\,l\cr \frac{1}{Z_0}\sinh\gamma\,l&\cosh\gamma\,l\end{bmatrix}\begin{bmatrix}E_R\cr 0\end{bmatrix}\\<br />&=&\begin{bmatrix}E_R\,\cosh\gamma\,l\cr \frac{E_R}{Z_0}\sinh\gamma\,l\end{bmatrix}<br />\end{eqnarray}$ 従って、送電端の電圧ESと受電端の電圧ERの比は $\begin{eqnarray}<br />\frac{E_R}{E_S}&=&\frac{1}{\cosh\gamma\,l}<br />\end{eqnarray}$ ということになる。ついでに $\begin{eqnarray}<br />\frac{\left\|E_R\right\|}{\left\|E_S\right\|}&=&\frac{2\,{e}^{\alpha\,l}}{\sqrt{\left( {e}^{2\,\alpha\,l}-1\right)^2 \,{\sin\left( \beta\,l\right) }^{2}+\left( {e}^{2\,\alpha\,l}+1\right)^2 \,{\cos\left( \beta\,l\right) }^{2}}}\\<br />&=&1.05<br />\end{eqnarray}$ と絶対値の比の条件にしてしまおう。ここで無損失線路の場合 $\begin{eqnarray}<br />\gamma&=&\alpha+j\,\beta=\sqrt{\left(R+j\,\omega\,L\right)\left(G+j\,\omega\,C\right)}=j\,\omega\,\sqrt{L\,C}\ \ \ \ \left(R=G=0\right)<br />&=&j\,\beta\\<br />\alpha&=&0\\<br />\beta&=&\omega\,\sqrt{L\,C}<br />\end{eqnarray}$ であるからして,これを代入すると $\begin{eqnarray}<br />\frac{\left\|E_R\right\|}{\left\|E_S\right\|}&=&\frac{1}{\cos\left( \omega\,\sqrt{L\,C}\,l\right)}\\<br />&=&1.05<br />\end{eqnarray}$ ということになる。従って受電端の電圧が送電端の電圧より5[%]高くなるlの条件は $\begin{eqnarray}<br />\cos\omega\,\sqrt{L\,C}\,l&=&\frac{1}{1.05}\\<br />l&=&\frac{1}{\omega\,\sqrt{L\,C}}\cos^{-1}\frac{1}{1.05}<br />\end{eqnarray}$ ということになる。だがしかしそこには伏兵がいた（；´Д｀）題意ではL,Cが与えられていないのである。どうすんだこれ（；´Д｀）慌てずに考えよう頓知を出すのだ。上の式は位相定数βを使って書き直すことができる $\begin{eqnarray}<br />l&=&\frac{1}{\beta}\cos^{-1}\frac{1}{1.05}<br />\end{eqnarray}$ 位相定数βと波長の関係式を思い出そう $\begin{eqnarray}<br />\lambda&=&\frac{v}{f}\\<br />&=&\frac{2\,\pi}{\beta}\\<br />\beta&=&\frac{\omega}{v}=\frac{2\,\pi\,f}{v}<br />\end{eqnarray}$ これを代入すると $\begin{eqnarray}<br />l&=&\frac{v}{2\,\pi\,f}\cos^{-1}\frac{1}{1.05}=\frac{3\time 10^5}{2\,\pi\,\time 60}\cos^{-1}\frac{1}{1.05}\\<br />&=&247\ [km]<br />v&=&3\time 10^5\ [km/s]<br />f&=&60\ [Hz]<br />\end{eqnarray}$ ということになる。波長と位相定数の関係式から以下の式も導かれるので、それを用いてもよい。 $\begin{eqnarray}<br />v&=&\frac{1}{\sqrt{L\,C}}<br />\end{eqnarray}$ 波の伝搬速度が光速という時点でLとCは真空の透磁率と誘電率となるので、そこから導くこともできるが、それはちょっと邪道くさい。まだ電磁気学を学んでいないならなおさら。やはりここは波長と位相定数の関係式を思い出すのが正当だろう。真空中の電磁波の伝搬速度についても常識として記憶しておく必要がありそうである。関係式を暗記するのには波長や速度、位相定数などの単位を合わせて記憶しておくと辻褄があるかどうか自己チェックできる。一九世紀の電磁気学理論はそうした単位系と理論式の辻褄合わせの世界である。 P.S 途中の電圧比の絶対値の式の導出過程は面倒なので省略したが、それを確かめるのは読者の課題としよう( ´∀`)

webadm	投稿日時: 2012-11-2 7:17
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	四端子定数次は分布定数回路の四端子定数の問題特性インピーダンスZ0=200[Ω]、減衰定数α=0,位相定数β=π/8[rad/m]なる長さl=4[m]に対する四端子定数を計算せよ。というもの。有限長の分布定数回路の四端子定数は $\begin{eqnarray}<br />{\bf F}&=&\begin{bmatrix}A&B\cr C&D\end{bmatrix}=\begin{bmatrix}\cosh\gamma\,l&Z_0\,\sinh\gamma\,l\cr \frac{1}{Z_0}\sinh\gamma\,l&\cosh\gamma\,l\end{bmatrix}=\begin{bmatrix}\cosh\left(\alpha+j\,\beta\right)\,l&Z_0\,\sinh\left(\alpha+j\,\beta\right)\,l\cr \frac{1}{Z_0}\sinh\left(\alpha+j\,\beta\right)\,l&\cosh\left(\alpha+j\,\beta\right)\,l\end{bmatrix}<br />\end{eqnarray}$ であるからして、これに題意の定数を代入すると $\begin{eqnarray}<br />\begin{bmatrix}A&B\cr C&D\end{bmatrix}&=&\begin{bmatrix}\cosh\left(j\,\frac{\pi}{8}\,4\right)&200\,\sinh\left(j\,\frac{\pi}{8}\,4\right)\cr \frac{1}{200}\sinh\left(j\,\frac{\pi}{8}\,4\right)&\cosh\left(j\,\frac{\pi}{8}\,4\end{bmatrix}=\begin{bmatrix}\cos\frac{\pi}{2}&j\,200\,\sin\frac{\pi}{2}\cr j\frac{1}{200}\sin\frac{\pi}{2}&\cos\frac{\pi}{2}\end{bmatrix}\\<br />&=&\begin{bmatrix}0 & j\,200\cr j\frac{1}{200}&0\end{bmatrix}<br />\end{eqnarray}$ ということになる。

webadm	投稿日時: 2012-11-2 8:50
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	等価回路次は分布定数回路の等価回路に関する問題特性インピーダンスZ0、伝搬定数γ、長さlの一様な線路のT形、π形および格子形等価回路を求めよ。というもの。有限長の分布定数回路が四端子定数と同じ四端子定数を持つT形、π形および格子形等価回路の素子定数を導けば良いことになる。二端子対回路の演習問題でT形、π形および格子形回路の四端子定数を導いた記憶があるが、詳細は定かではない。つまり忘れてしまったということである。なのでそれを思い出すことから始めねばならない。 T形とπ形は３つの二端子対回路を縦続接続させたものとして考えれば簡単に導くことができる。 $\begin{eqnarray}<br />{\bf F_T}&=&\begin{bmatrix}1&Z_1\cr 0&1\end{bmatrix}\begin{bmatrix}1& 0\cr \frac{1}{Z_2}& 1\end{bmatrix}\begin{bmatrix}1&Z_3\cr 0&1\end{bmatrix}\\<br />&=&\begin{bmatrix}\frac{{Z}_{2t}+{Z}_{1T}}{{Z}_{2t}} & \frac{{Z}_{2t}\,{Z}_{3}+{Z}_{1t}\,{Z}_{3t}+{Z}_{1t}\,{Z}_{2t}}{{Z}_{2t}}\cr \frac{1}{{Z}_{2t}} & \frac{{Z}_{3t}+{Z}_{2t}}{{Z}_{2t}}\end{bmatrix}<br />\end{eqnarray}$ 分布定数回路は対称回路なので、T形回路ではZ1t=Z3tとなり $\begin{eqnarray}<br />{\bf F_T}&=&\begin{bmatrix}\frac{{Z}_{2t}+{Z}_{1t}}{{Z}_{2t}} & 2\,Z_{1t}+\frac{{Z_{1t}}^2}{Z_{2t}}\cr \frac{1}{{Z}_{2t}} & \frac{{Z}_{2t}+{Z}_{1t}}{{Z}_{2t}}\end{bmatrix}<br />\end{eqnarray}$ ということになる。同様にπ形回路は $\begin{eqnarray}<br />{\bf F_{\pi}}&=&\begin{bmatrix}1&0\cr \frac{1}{Z_{1\pi}} & 1\end{bmatrix}\begin{bmatrix}1&Z_{2\pi}\cr 0&1\end{bmatrix}\begin{bmatrix}1&0\cr \frac{1}{Z_{3\pi}}&1\end{bmatrix}\\<br />&=&\begin{bmatrix}\frac{{Z}_{3\pi}+{Z}_{2\pi}}{{Z}_{3\pi}} & {Z}_{2\pi}\cr \frac{{Z}_{3\pi}+{Z}_{2\pi}+{Z}_{1\pi}}{{Z}_{1\pi}\,{Z}_{3\pi}} & \frac{{Z}_{2\pi}+{Z}_{1\pi}}{{Z}_{1\pi}}\end{bmatrix}<br />\end{eqnarray}$ ということになる。これも同様に対称回路であるためにはZ1π=Z3πとなり $\begin{eqnarray}<br />{\bf F_{\pi}}&=&\begin{bmatrix}\frac{{Z}_{1\pi}+{Z}_{2\pi}}{{Z}_{1\pi}} & {Z}_{2\pi}\cr \frac{2\pi}{Z_{1\pi}}+\frac{Z_{2\pi}}{{{Z}_{1\pi}}^2} & \frac{{Z}_{1\pi}+{Z}_{2\pi}}{{Z}_{1\pi}}\end{bmatrix}<br />\end{eqnarray}$ ということになる。さて格子形回路の四端子定数はどうだっただろう。かなり苦労した覚えがある。出力端を開放および短絡した場合のそれぞれの駆動点インピーダンスZo,Zsと四端子定数の関係を思い出そう $\begin{eqnarray}<br />\begin{bmatrix}E_S\cr I_S\end{bmatrix}&=&\begin{bmatrix}A&B\cr C&D\end{bmatrix}\begin{bmatrix}E_R\cr 0\end{bmatrix}\\<br />&=&\begin{bmatrix}A\,E_R\cr C\,E_R\end{bmatrix}\\<br />Z_o&=&\frac{E_S}{I_S}=\frac{A\,\cancel{E_R}}{B\,\cancel{E_R}}\\<br />&=&\frac{A}{C}<br />\end{eqnarray}$ $\begin{eqnarray}<br />\begin{bmatrix}E_S\cr I_S\end{bmatrix}&=&\begin{bmatrix}A&B\cr C&D\end{bmatrix}\begin{bmatrix}0\cr I_R\end{bmatrix}\\<br />&=&\begin{bmatrix}C\,I_R\cr D\,I_R\end{bmatrix}\\<br />Z_s&=&\frac{E_R}{I_R}=\frac{B\,\cancel{I_R}}{D\,\cancel{I_R}}\\<br />&=&\frac{B}{D}<br />\end{eqnarray}$ 負荷に特性インピーダンスZ0を接続した場合、駆動点インピーダンスも特性インピーダンスと等しくなることから $\begin{eqnarray}<br />\begin{bmatrix}E_S\cr I_S\end{bmatrix}&=&\begin{bmatrix}A&B\cr C&D\end{bmatrix}\begin{bmatrix}Z_0\,I_R\cr I_R\end{bmatrix}\\<br />&=&\begin{bmatrix}I_R\,\left(A\,Z_0+B\right)\cr I_R\left(C\,Z_0+D\right)\end{bmatrix}\\<br />Z_0&=&\frac{\cancel{I_R}\left(A\,Z_0+B\right)}{\cancel{I_R}\left(C\,Z_0+D\right)}\\<br />&=&\frac{A\,Z_0+B}{C\,Z_0+D}\\<br />C\,{Z_0}^2-\left(A-D\right)Z_0-B&=&C\,\left(\left(Z_0-\frac{A-D}{2\,C}\right)^2-\left(\left(\frac{A-D}{2\,C}\right)^2+\frac{B}{C}\right)=0\\<br />Z_0&=&\frac{A-D\pm\sqrt{\left(A-D\right)^2+4\,B\,C}}{2\,C}<br />\end{eqnarray}$ ここで対称回路ではA=Dであるので $\begin{eqnarray}<br />Z_0&=&\pm\sqrt{\frac{B}{C}}=\pm\sqrt{Z_s\,Z_o}<br />\end{eqnarray}$ ということになる。Z0,Zs,Zoは一般に複素数なのでZ0は曖昧で±はそのままにしてある。無損失線路か無歪線路の場合Z0は正の実数になる。ここで四端子定数の関係式から $\begin{eqnarray}<br />A\,D-B\,C&=&A^1-B\,C=1\\<br />Z_o&=&\frac{A}{C}\\<br />Z_s&=&\frac{B}{A}<br />\end{eqnarray}$ よりA,B,Cを解くと $\begin{eqnarray}<br />{\bf F_{L}}&=&\begin{bmatrix}A&B\cr C&D\end{bmatrix}=\begin{bmatrix}\pm\frac{\sqrt{{Z}_{o}}}{\sqrt{{Z}_{o}-{Z}_{s}}}&\pm\frac{\sqrt{{Z}_{o}}\,{Z}_{s}}{\sqrt{{Z}_{o}-{Z}_{s}}}\cr \pm\frac{\sqrt{{Z}_{o}-{Z}_{s}}}{\sqrt{{Z}_{o}}\,\left( {Z}_{o}-{Z}_{s}\right) }&\pm\frac{\sqrt{{Z}_{o}}}{\sqrt{{Z}_{o}-{Z}_{s}}}\end{bmatrix}<br />\end{eqnarray}$ ということになる。これに対称格子形回路の開放および短絡駆動点インピーダンスを求めて代入すると $\begin{eqnarray}<br />{\bf F_{L}}&=&\begin{bmatrix}\pm\frac{{Z}_{2}+{Z}_{1}}{{Z}_{2}-{Z}_{1}}&\pm\frac{2\,{Z}_{1}\,{Z}_{2}}{{Z}_{2}-{Z}_{1}}\cr \pm\frac{2}{{Z}_{2}-{Z}_{1}}&\pm\frac{{Z}_{2}+{Z}_{1}}{{Z}_{2}-{Z}_{1}}\end{bmatrix}<br />\end{eqnarray}$ ということになる。 Z1,Z2は一般に複素数であるので曖昧性があり、±はそのまま残してある。Z1,Z2が純抵抗の場合にはZ1>Z2の場合には-をとることになる。さてここまでは準備段階に過ぎない。いよいよそれぞれの等価回路の四端子定数を導く段階にはいる。分布定数回路と上の３つの等価回路は同値であるためには $\begin{eqnarray}<br />{\bf F}&=&\begin{bmatrix}\cosh\gamma\,l&Z_0\,\sinh\gamma\,l\cr \frac{1}{Z_0}\sinh\gamma\,l&\cosh\gamma\,l\end{bmatrix}\\<br />&=&{\bf F_T}=\begin{bmatrix}\frac{{Z}_{2t}+{Z}_{1t}}{{Z}_{2t}} & 2\,Z_{1t}+\frac{{Z_{1t}}^2}{Z_{2t}}\cr \frac{1}{{Z}_{2t}} & \frac{{Z}_{2t}+{Z}_{1t}}{{Z}_{2t}}\end{bmatrix}\\<br />&=&{\bf F_{\pi}}=\begin{bmatrix}\frac{{Z}_{1\pi}+{Z}_{2\pi}}{{Z}_{1\pi}} & {Z}_{2\pi}\cr \frac{2}{Z_{1\pi}}+\frac{Z_{2\pi}}{{{Z}_{1\pi}}^2} & \frac{{Z}_{1\pi}+{Z}_{2\pi}}{{Z}_{1\pi}}\end{bmatrix}\\<br />&=&{\bf F_{L}}=\begin{bmatrix}\pm\frac{{Z}_{2}+{Z}_{1}}{{Z}_{2}-{Z}_{1}}&\pm\frac{2\,{Z}_{1}\,{Z}_{2}}{{Z}_{2}-{Z}_{1}}\cr \pm\frac{2}{{Z}_{2}-{Z}_{1}}&\pm\frac{{Z}_{2}+{Z}_{1}}{{Z}_{2}-{Z}_{1}}\end{bmatrix}<br />\end{eqnarray}$ を満たすZ1t,Z2t,Z1π,Z2π,それにZ1,Z2が存在することである。すなわち $\begin{eqnarray}<br />Z_{2t}\left(1-\cosh\gamma\,l\right)+Z_{1t}&=&0\\<br />Z_{2t}\left(2\,Z_{1t}-Z_0\,\sinh\gamma\,l\right)+Z_{1t}^2&=&0\\<br />Z_0-Z_{2t}\,\sinh\gamma\,l&=&0<br />\end{eqnarray}$ のいずれか２つの式をZ1t,Z2tに関する連立方程式として解くと。 $\begin{eqnarray}<br />Z_{1t}&=&\frac{{Z}_{0}\,\sinh\gamma\,l }{\cosh\gamma\,l+1}=\frac{{Z}_{0}\,\left(\cosh\gamma\,l -1\right)}{\sinh\gamma\,l}\\<br />&=&Z_0\,\tanh\frac{\gamma\,l}{2}\\<br />Z_{2t}&=&\frac{{Z}_{0}}{\sinh\gamma\,l}<br />\end{eqnarray}$ と言う結果が得られる。Z1tについては最後に半数の双曲線関数の公式を使った。同様にπ形回路に関しても $\begin{eqnarray}<br />Z_{1\pi}\left(1-\cosh\gamma\,l\right)+Z_{2\pi}&=&0\\<br />Z_{2\pi}-Z_0\,\sinh\gamma\,l&=&0\\<br />Z_0\left(2\,Z_{1\pi}+Z_{2\pi}\right)-Z_{1\pi}^2\,\sinh\gamma\,l&=&0<br />\end{eqnarray}$ のいずれか２つの式をZ1π,Z2πに関する連立方程式として解くと。 $\begin{eqnarray}<br />Z_{1\pi}&=&\frac{{Z}_{0}\,\sinh\gamma\,l }{\cosh\gamma\,l -1}=\frac{{Z}_{0}\,\left(\cosh\gamma\,l +1\right)}{\sinh\gamma\,l }\\<br />&=&Z_0\,\coth\frac{\gamma\,l}{2}\\<br />Z_{2\pi}&=&{Z}_{0}\,\sinh\gamma\,l<br />\end{eqnarray}$ などという結果が得られる。Z1πに関しては同様に半数の双曲線関数の公式を使った。最後格子形回路についても $\begin{eqnarray}<br />\pm\left(Z_1+Z_2\right)-\left(Z_2-Z_1\right)\cosh\gamma\,l&=&0\\<br />\pm\,2\,Z_1\,Z_2-\left(Z_2-Z_1\right)Z_0\,sinh\gamma\,l&=&0\\<br />\pm\,2\,Z_0-\left(Z_2-Z_1\right)\sinh\gamma\,l&=&0<br />\end{eqnarray}$ のいずれか２つの式をZ1,Z2に関する連立方程式として解くと。 $\begin{eqnarray}<br />Z_1&=&\frac{{Z}_{0}\,\left(\cosh\gamma\,l -1\right)}{\sinh\gamma\,l}\\<br />&=&Z_0\,\tanh\frac{\gamma\,l}{2}\\<br />Z_2&=&\frac{{Z}_{0}\,\sinh\gamma\,l }{\cosh\gamma\,l -1}\\<br />&=&Z_0\,\coth\frac{\gamma\,l}{2}<br />\end{eqnarray}$ などという結果が得られる。実は上のZ1T,Z2T,Z1π,Z2π、それにZ1,Z2にはそれぞれ二次方程式のため２つの解が存在する。そのどちらでも元の方程式を満足するのだが、はてさてこれはどうしたものだろう。同値の２つの回路が存在するということになる。この疑問についての答えを出すのは読者の課題としよう( ´∀`) P.S もちろん受動素子だけで構成する場合には、インピーダンスの実数部は負とならないため、上の結果でよいことなる。しかし受動素子に限らないならば、インピーダンスの実数部が負になってもよいのである。

webadm	投稿日時: 2012-11-3 8:48
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	影像インピーダンス、伝達定数次は影像インピーダンスと伝達定数に関する問題長さ1[km]当り、特性インピーダンスZ0=20+j15[Ω]、伝搬定数γ=0.01+j0.003の線路がl=50[km]ある。この線路の影像インピーダンスZ01,Z02および伝達定数θを求めよ。というもの。影像インピーダンスも伝達定数も二端子対回路で学んだのを思い出す必要がある。元来影像インピーダンスは非対称な集中定数回路で定義されていてZ01,Z02と２つある。しかし二端子対回路で学んだように、対称回路では入力端と出力端を取り替えても回路は同じなので２つの影像インピーダンスは同値となる。二端子対回路の時に独自に非対称な伝送回路を互いに背中合わせに縦続接続すると、二種類の対称回路ができることから、その伝送行列の固有ベクトルの成分が影像インピーダンスに相当し、固有値の自然対数が回路２つ分の伝達係数となることを再発見した。対称回路の伝送行列の固有ベクトルの成分は影像インピーダンスであると同時に特性インピーダンスでもある。ここではそれを再掲するつもりはないが、結果だけ利用することにしよう。すなわち一様な線路の特性インピーダンスは対称回路の影像インピーダンスと等しい。 $\begin{eqnarray}<br />Z_{01}&=&Z_{02}=Z_0<br />\end{eqnarray}$ ここで分布定数回路の伝送行列の固有ベクトルと固有値として特性インピーダンスと伝達係数を導くと $\begin{eqnarray}<br />{\bf F}{\bf X}&=&\lambda\,{\bf X}\\<br />\left({\bf F}-\lambda\,{\bf E}\right){\bf X}&=&\begin{bmatrix}\cosh\gamma\,l-\lambda&Z_0\,\sinh\gamma\,l\cr \frac{1}{Z_0}\sinh\gamma\,l&\cosh\gamma\,l-\lambda\end{bmatrix}{\bf X}=0\\<br />\left(\cosh\gamma\,l-\lambda\right)^2-\sinh^{2}\gamma\,l&=&0\\<br />\lambda&=&\cosh\gamma\,l\pm\sinh\gamma\,l=\frac{e^{\gamma\,l}+e^{-\gamma\,l}}{2}\pm\frac{e^{\gamma\,l}-e^{-\gamma\,l}}{2}=e^{\pm\gamma\,l}\\<br />&=&e^{\gamma\,l}\ \ \ \ \left(Re\left(\gamma\right)=\alpha\ge 0\right)\\<br />\theta&=&\gamma\,l\\<br />\begin{bmatrix}\cosh\gamma\,l- e^{\gamma\,l}&Z_0\,\sinh\gamma\,l\cr \frac{1}{Z_0}\sinh\gamma\,l&\cosh\gamma\,l- e^{\gamma\,l}\end{bmatrix}\begin{bmatrix}X_1\cr X_2\end{bmatrix}&=&\begin{bmatrix}X_1\left(\cosh\gamma\,l- e^{\gamma\,l}\right)+X_2\,Z_0\,\sinh\gamma\,l\cr \frac{X_1}{Z_0}\sinh\gamma\,l+X_2\left(\cosh\gamma\,l- e^{\gamma\,l}\right)\end{bmatrix}=\begin{bmatrix}0\cr 0\end{bmatrix}\\<br />{\bf X}&=&\begin{bmatrix}X_1\cr X_2\end{bmatrix}=\begin{bmatrix}Z_0\,X_2\cr \frac{X_1}{Z_0}\end{bmatrix}\\<br />&=&\begin{bmatrix}Z_0\cr 1\end{bmatrix}\ \ \ \ \left(X_2=1\right)\\<br /><br />\lambda&=&e^{\theta}\\<br />\theta&=&\ln\lambda\\<br />\end{eqnarray}$ ということになる。伝達定数は固有値の自然対数γlで固有ベクトルの成分は特性インピーダンスに他ならなかったことが確認できた。従って題意の数値を代入すると $\begin{eqnarray}<br />Z_{01}&=&Z_{02}=Z_0=20+j15\ [\Omega]\\<br />\theta&=&\left(0.01+j\,0.003\right)\time 50=0.5+j\,0.15<br />\end{eqnarray}$ ということになる。 P.S 伝送行列の固有値と固有ベクトルにはそれぞれ曖昧性がある。常識的には入力端から供給される電力よりもは出力端に供給される電力が増えることはないし、インピーダンスの実数部は常に正をとるように選ぶ。しかしそれとは双対なもうひとつの世界があることも忘れてはならないのである。

webadm	投稿日時: 2012-11-4 1:46
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	線路定数の異なる２つの分布定数回路の接続次は異なる分布定数回路の接続に関する問題下図の回路の送電端インピーダンスZsを求めよ。ただし各線路の特性インピーダンスをZ01,Z02、位相定数をβ1,β2とする。というもの。２つの線路をそれぞれ二端子対回路として考えればその縦続接続として簡単に結果は得られるが別解でやってみよう。最初に受電端に近い方の線路だけを考えて、その送電端インピーダンスを求めれば、それがもう一方の線路の受電端に接続されているのと等価であるという事実を利用する。線路２の送電端インピーダンスをZs02とすると $\begin{eqnarray}<br />\begin{bmatrix}E_{s02}\cr I_{s02}\end{bmatrix}&=&\begin{bmatrix}\cosh\left(j\,\beta_2\,l_2\right)&Z_{02}\,\sinh\left(j\,\beta_2\,l_2\right)\cr \frac{1}{Z_{02}}\sinh\left(j\,\beta_2\,l_2\right)&\cosh\left(j\,\beta_2\,l_2\right)\end{bmatrix}\begin{bmatrix}E_R\cr 0\end{bmatrix}\\<br />&=&\begin{bmatrix}E_R\,\cos\beta_2\,l_2\cr j\,\frac{E_R}{Z_{02}}\sin\beta_2\,l_2\end{bmatrix}\\<br />Z_{s02}&=&\frac{E_{s02}}{I_{s02}}=\frac{E_{r01}}{I_{r01}}=\frac{\cancel{E_R}\,\cos\beta_2\,l_2}{j\frac{\cancel{E_R}}{Z_{02}}\sin\beta_2\,l_2}\\<br />&=&-j\,Z_{02}\cot\beta_2\,l_2<br />\end{eqnarray}$ ということになる。あとは線路１の受電端にZs02が接続されている場合の送電端インピーダンスを求めればよいことになる。 $\begin{eqnarray}<br />\begin{bmatrix}E_S\cr I_S\end{bmatrix}&=&\begin{bmatrix}\cosh\left(j\,\beta_1\,l\right)&Z_{01}\,\sinh\left(j\,\beta_1\,l\right)\cr \frac{1}{Z_{01}}\sinh\left(beta_1\,l\right)&\cosh\left(j\,\beta_1\,l\right)\end{bmatrix}\begin{bmatrix}Z_{s02}I_{r01}\cr I_{r01}\end{bmatrix}\\<br />&=&\begin{bmatrix}\cos\beta_1\,l_1&j\,Z_{01}\sin\beta_1\,l_1\cr j\frac{1}{Z_{01}}\sin\beta_1\,l_1&\cos\beta_1\,l_1\end{bmatrix}\begin{bmatrix}-j\,I__{r01}\,Z_{02}\cot\beta_2\,l_2\cr I_{r01}\end{bmatrix}\\<br />&=&\begin{bmatrix}j\,I_{r01}\left(Z_{01}\,\sin\beta_1\,l_1-Z_{02}\,\cos\beta_1\,l_1\,\cot\beta_2\,l_2\right)\cr I_{r01}\left(\frac{Z_{02}}{Z_{01}}\sin\beta_1\,l_1\,\cot\beta_2\,l_2+\cos\beta_1\,l_1\right)\end{bmatrix}\\<br />Z_s&=&\frac{E_S}{I_S}=\frac{j\,\cancel{I_{r01}}\left(Z_{01}\,\sin\beta_1\,l_1-Z_{02}\,\cos\beta_1\,l_1\,\cot\beta_2\,l_2\right)}{\cancel{I_{r01}}\left(\frac{Z_{02}}{Z_{01}}\sin\beta_1\,l_1\,\cot\beta_2\,l_2+\cos\beta_1\,l_1\right)}=j\,Z_{01}\frac{\cancel{\cos\beta_1\,l_1\,\cot\beta_2\,l_2}\,\left(Z_{01}\frac{\sin\beta_1\,l_1}{\cos\beta_1\,l_1\,\cot\beta_2\,l_2}-Z_{02}\right)}{\cancel{\cos\beta_1\,l_1\,\cot\beta_2\,l_2}\,\left(Z_{02}\frac{\sin\beta_1\,l_1}{\cos\beta_1\,l_1}+Z_{01}\frac{1}{\cot\beta_2\,l_2}\right)}\\<br />&=&j\,Z_{01}\frac{Z_{01}\tan\beta_1\,l_1\,\tan\beta_2\,l_2-Z_{02}}{Z_{02}\tan\beta_1\,l_1+Z_{01}\tan\beta_2\,l_2}<br />\end{eqnarray}$ ということになる。他にも任意の位置でのインピーダンスが得られる位置角を用いた解法があるので、それは読者の課題としよう( ´∀`)

webadm	投稿日時: 2012-11-4 2:28
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	位置角次は位置角に関する問題特性インピーダンスZ0=50[Ω]の無損失線路を負荷ZR=100+j50[Ω]で終端したとき、受電端より900[m]の点のインピーダンスZを求めよ。ただし周波数は1[MHz]とする。というもの。線路上の任意の位置のインピーダンスを求める問題なので出題者は当然ながら位置角を用いて解くことを期待しているが、天の邪鬼なので位置角を使わず解いてみよう。前問の場合で２つの線路が同じ線路定数を持ち長さだけ異なると考えればよいのである。受電端に近い方の長さl2の線路の送電端インピーダンスを求めればよいわけである。受信端から長さl2の位置で以下の関係が成り立つ $\begin{eqnarray}<br />\begin{bmatrix}E_{s02}\cr I_{s02}\end{bmatrix}&=&\begin{bmatrix}\cosh\left(j\,\beta_2\,l_2\right)&Z_{02}\,\sinh\left(j\,\beta_2\,l_2\right)\cr \frac{1}{Z_{02}}\sinh\left(j\,\beta_2\,l_2\right)&\cosh\left(j\,\beta_2\,l_2\right)\end{bmatrix}\begin{bmatrix}Z_{R}\,I_R\cr I_R\end{bmatrix}\\<br />&=&\begin{bmatrix}\cos\beta_2\,l_2&j\,Z_{02}\,\sin\beta_2\,l_2\cr j\,\frac{1}{Z_{02}}\sin\beta_2\,l_2&\cos\beta_2\,l_2\end{bmatrix}\begin{bmatrix}Z_R\,I_R\cr I_R\end{bmatrix}\\<br />&=&\begin{bmatrix}I_R\,\left(Z_R\,\cos\beta_2\,l_2+j\,Z_{02}\,\sin\beta_2\,l_2\right)\cr I_R\left(\cos\beta_2\,l_2+j\frac{Z_R}{Z_{02}}\sin\beta_2\,l_2\right)\end{bmatrix}\\<br />Z&=&\frac{E_{s02}}{I_{s02}}=\frac{\cancel{I_R}\,\left(Z_R\,\cos\beta_2\,l_2+j\,Z_{02}\,\sin\beta_2\,l_2\right)}{\cancel{I_R}\left(\cos\beta_2\,l_2+j\frac{Z_R}{Z_{02}}\sin\beta_2\,l_2\right)}=Z_{02}\frac{Z_R\,\cos\beta_2\,l_2+j\,Z_{02}\,\sin\beta_2\,l_2}{Z_{02}\,\cos\beta_2\,l_2+j\,Z_R\,\sin\beta_2\,l_2}=Z_{02}\frac{\cancel{\cos\beta_2\,l_2}\left(Z_R+j\,Z_{02}\frac{\sin\beta_2\,l_2}{\cos\beta_2\,l_2}\right)}{\cancel{\cos\beta_2\,l_2}\left(Z_{02}+j\,Z_R\,\frac{\sin\beta_2\,l_2}{\cos\beta_2\,l_2}\right)}\\<br />&=&Z_{02}\,\frac{Z_R+j\,Z_{02}\,\tan\beta_2\,l_2}{Z_{02}+j\,Z_R\,\tan\beta_2\,l_2}\\<br />&=&Z_{02}\,\frac{Z_R+j\,Z_{02}\,\tan\frac{2\,\pi\,f\,l_2}{v}}{Z_{02}+j\,Z_R\,\tan\frac{2\,\pi\,f\,l_2}{v}}\\<br />\beta_2&=&\frac{2\,\pi}{\lambda}=\frac{2\,\pi,f}{v}<br />\lambda&=&\frac{v}{f}<br />\end{eqnarray}$ これに題意の定数を代入すると $\begin{eqnarray}<br />Z&=&50\,\frac{100+j\,50+j\,50\,\tan\frac{2\,\pi\time 10^6\time 900}{3\time 10^8}}{50+j\,\left(100+j\,50\right)\tan\frac{2\,\pi\time 10^6\time 900}{3\time 10^8}}=\cancel{50}\,\frac{100+j\,50}{\cancel{50}}\\<br />&=&100+j\,50\ [\Omega]<br />\end{eqnarray}$ ということになる。なんだ受電端の負荷と同じじゃん( ´∀`) 一瞬計算間違いしたのかと思った。問題設定の受電端の距離だとちょうど波長の整数倍になるので無損失線路の場合は、受電端のインピーダンスと等しくなるというからくりであった。

webadm	投稿日時: 2012-11-4 3:34
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	続：位置角次もどうやら位置角に関する問題らすい特性インピーダンス、伝搬定数および長さがそれぞれ、Z01,γ1,l1およびZ02,γ2,l2なる線路を下図に示すように接続した。電圧Eなる電源から流出する電流を求めよ。というもの。これも位置角を用いないで別解でやってみよう。線路１と線路２をそれぞれ二端子対回路として見ると、それぞれの送電端から見たインピーダンスZs01,Zs02は $\begin{eqnarray}<br />\begin{bmatrix}E_{s01}\cr I_{s01}\end{bmatrix}&=&\begin{bmatrix}\cosh\gamma_1\,l_1&Z_{01}\,\sinh\gamma_1\,l_1\cr \frac{1}{Z_{01}}\,\sinh\gamma_1\,l_1&\cosh\gamma_1\,l_1\end{bmatrix}\begin{bmatrix}E_R\cr 0\end{bmatrix}\\<br />&=&\begin{bmatrix}E_R\,\cosh\gamma_1\,l_1\cr \frac{E_R}{Z_{01}}\,\sinh\gamma_1\,l_1\end{bmatrix}\\<br />Z_{s01}&=&\frac{E_{s01}}{I_{s01}}=\frac{\cancel{E_R}\,\cosh\gamma_1\,l_1}{\frac{\cancel{E_R}}{Z_{01}}\,\sinh\gamma_1\,l_1}\\<br />&=&Z_{01}\,\coth\gamma_1\,l_1<br />\end{eqnarray}$ $\begin{eqnarray}<br />\begin{bmatrix}E_{s02}\cr I_{s02}\end{bmatrix}&=&\begin{bmatrix}\cosh\gamma_2\,l_2&Z_{02}\,\sinh\gamma_2\,l_2\cr \frac{1}{Z_{02}}\,\sinh\gamma_2\,l_2&\cosh\gamma_2\,l_2\end{bmatrix}\begin{bmatrix}Z_R\,I_R\cr I_R\end{bmatrix}\\<br />&=&\begin{bmatrix}I_R\left(Z_R\,\cosh\gamma_2\,l_2+Z_{02}\,\sinh\gamma_2\,l_2\right)\cr I_R\left(\frac{Z_R}{Z_{02}}\,\sinh\gamma_2\,l_2+\cosh\gamma_2\,l_2\right)\end{bmatrix}\\<br />Z_{s02}&=&\frac{E_{s02}}{I_{s02}}=\frac{\cancel{I_R}\left(Z_R\,\cosh\gamma_2\,l_2+Z_{02}\,\sinh\gamma_2\,l_2\right)}{\cancel{I_R}\left(\frac{Z_R}{Z_{02}}\,\sinh\gamma_2\,l_2+\cosh\gamma_2\,l_2\right)}=Z_{02}\,\frac{\cancel{Z_{02}\,\cosh\gamma_2\,l_2}\,\left(\frac{Z_R}{Z_{02}}+\frac{\sinh\gamma_2\,l_2}{\cosh\gamma_2\,l_2}\right)}{\cancel{Z_{02}\,\cosh\gamma_2\,l_2}\,\left(\frac{Z_R}{Z_{02}}\,\sinh\gamma_2\,l_2+1\right)}=Z_{02}\,\frac{\tanh\theta+\tanh\gamma_2\,l_2}{\tanh\theta\,\tanh\gamma_2\,l_2+1}\\<br />&=&Z_{02}\,\tanh\left(\gamma_2\,l_2+\tanh^{-1}\frac{Z_R}{Z_{02}}\right)\\<br />\tanh\theta&=&\frac{Z_R}{Z_{02}}<br />\end{eqnarray}$ ということになる。従って以下の様な等価回路が得られる。従って電源から流れる電流Iは $\begin{eqnarray}<br />I&=&\frac{E}{Z_{s01}+Z_{s02}}=\frac{E}{Z_{01}\,\coth\gamma_1\,l_1+Z_{02}\,\tanh\left(\gamma_2\,l_2+\tanh^{-1}\frac{Z_R}{Z_{02}}\right)}<br />\end{eqnarray}$ ということになる。 Zs02の最後では双曲線関数のtanhの加法定理の公式を用いた。

webadm	投稿日時: 2012-11-4 4:39
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	続々：位置角次も位置角に関する問題らすい下図のような特性インピーダンスZ0、伝搬定数γ、長さlの線路の受電端を短絡し、線路の中央に抵抗Rを挿入するとき、送電点のインピーダンスZsはいくらになるか。というもの。これは前問の電源を抵抗Rに、負荷を短絡に変えたような感じの回路である。出題者は位置角を用いて解くことを期待しているが、天の邪鬼なので位置角を用いない方法で解いてみよう。これも二端子対回路を縦続させたものと考えれば $\begin{eqnarray}<br />\begin{bmatrix}E_S\cr I_S\end{bmatrix}&=&\begin{bmatrix}\cosh\frac{\gamma\,l}{2}&Z_0\,\sinh\frac{\gamma\,l}{2}\cr \frac{1}{Z_0}\,\sinh\frac{\gamma\,l}{2}&\cosh\frac{\gamma\,l}{2}\end{bmatrix}\begin{bmatrix}1&R\cr 0&1\end{bmatrix}\begin{bmatrix}\cosh\frac{\gamma\,l}{2}&Z_0\,\sinh\frac{\gamma\,l}{2}\cr \frac{1}{Z_0}\,\sinh\frac{\gamma\,l}{2}&\cosh\frac{\gamma\,l}{2}\end{bmatrix}\begin{bmatrix}0\cr I_R\end{bmatrix}\\<br />&=&\begin{bmatrix}{I}_{R}\,\cosh\left( \frac{\gamma\,l}{2}\right) \,\left( 2\,{Z}_{0}\,\sinh\left( \frac{\gamma\,l}{2}\right) +R\,\cosh\left( \frac{\gamma\,l}{2}\right) \right) \cr \frac{{I}_{R}\,\left( {Z}_{0}\,{\sinh\left( \frac{\gamma\,l}{2}\right) }^{2}+R\,\cosh\left( \frac{\gamma\,l}{2}\right) \,\sinh\left( \frac{\gamma\,l}{2}\right) +{Z}_{0}\,{\cosh\left( \frac{\gamma\,l}{2}\right) }^{2}\right) }{{Z}_{0}}\end{bmatrix}\\<br />Z_S&=&\frac{E_S}{I_S}=\frac{\cancel{{I}_{R}}\,\cosh\left( \frac{\gamma\,l}{2}\right) \,\left( 2\,{Z}_{0}\,\sinh\left( \frac{\gamma\,l}{2}\right) +R\,\cosh\left( \frac{\gamma\,l}{2}\right) \right)}{\frac{\cancel{{I}_{R}}\,\left( {Z}_{0}\,{\sinh\left( \frac{\gamma\,l}{2}\right) }^{2}+R\,\cosh\left( \frac{\gamma\,l}{2}\right) \,\sinh\left( \frac{\gamma\,l}{2}\right) +{Z}_{0}\,{\cosh\left( \frac{\gamma\,l}{2}\right) }^{2}\right) }{{Z}_{0}}}=\frac{\cancel{\cosh^2\left( \frac{\gamma\,l}{2}\right)} \,\left( 2\,{Z}_{0}\,\frac{\sinh\left( \frac{\gamma\,l}{2}\right)}{\cosh\left(\frac{\gamma\,l}{2}\right)} +R \right)}{\cancel{\cosh^2\left( \frac{\gamma\,l}{2}\right)} \,\left( \frac{{\sinh^2\left( \frac{\gamma\,l}{2}\right) }}{\cosh^2\left(\frac{\gamma\,l}{2}\right)}+\frac{R}{Z_0}\,\frac{\sinh\left( \frac{\gamma\,l}{2}\right)}{\cosh\left(\frac{\gamma\,l}{2}\right)} +1\right)}=\frac{2\,Z_0\,\tanh\left(\frac{\gamma\,l}{2}\right)+R}{\tanh^2\left(\frac{\gamma\,l}{2}\right)+\frac{R}{Z_0}\,\tanh\left(\frac{\gamma\,l}{2}\right)+1}\\<br />&=&\frac{2\,Z_0\,\tanh\left(\frac{\gamma\,l}{2}\right)+R}{\tanh\left(\frac{\gamma\,l}{2}\right)\,\left(\frac{R}{Z_0}+\tanh\left(\frac{\gamma\,l}{2}\right)\right)+1}<br />\end{eqnarray}$ ということになる。双曲線関数の倍角の公式を用いればγl/2が無くなってγlだけの双曲線関数だけの式にできるが。しかしtanhだけ用いた上の結果の方が良いと思われる。線路の途中に抵抗Rを入れた場合には、単純に入れない場合の線路の送電端インピーダンスにRを加えたものにはならないのである。よく理解していない受験者への有る意味引っかけ問題かもしれない。抵抗でなく線路の途中にLやCを入れた場合についてどうなるかは読者の課題としよう( ´∀`)

webadm	投稿日時: 2012-11-4 5:07
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	反射係数、透過係数次は反射係数と透過係数の公式を導出する問題。これは理論の時に既にやってしまったので、割愛。

webadm	投稿日時: 2012-11-10 19:36
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3089	反射係数次は反射係数に関する問題。線路上を点xが正方向に移動するとき、反射係数mvはどのように変化するか。というもの。送電端の位置をx=0とすると、受電端に関する条件は与えられていないので、反射係数は送電端からの距離xに関して一意的に定義される等価反射係数Γ(x)の意であると解釈される。理論のときに等価反射係数は送電端からの位置xによって二分された線路のそれぞれの特性インピーダンスからなる有理形関数として表されることを学んだ。題意としては具体的な反射係数を導くのではなく、それをxの関数として表した場合にどのような性質を持つか洞察せよという意味にとれる。ここでこれまで学んだ結果をまとめるとむう、ここからだいぶ長々と書き込みしていたのだが諸事情で古いWindows 2000ノートPCのFirefox環境から書き込んでいたら、ご丁寧にセッションタイムアウトを通知する画面を表示する供にFirefoxはそれまで書き込んでいたテキストを破棄しやがった。そういえばこれがあるからFirefoxからGoogle Chromeに鞍替えしたんだった。もう二度と使うものか>Firefox Chromeだとセッションタイムアウトを過ぎても何も言ってこないが、送信時にセッションタイムアウトとわかり、書き込めなかったページ内容は「戻る」で送信直前のページ内容が再表示される。長い時間かけて書き込み内容を用意したり、用意している途中に席をたったりしてセッションタイムアウトになっても安心である。なんの話だったっけ、ああ問題の解答内容ね。また書き直そう。最初から考えると、同じ線路を点xで２つの線路に分かれることになる。ここで以下の関係が成り立つ $\begin{eqnarray}<br />V\left(x\right)&=&V_i\left(x\right)+V_r\left(x\right)=A\,e^{-\gamma\,x}+B\,e^{\gamma\,x}\\<br />I\left(x\right)&=&I_i\left(x\right)-I_r\left(x\right)=\frac{V_i\left(x\right)-V_r\left(x\right)}{Z_0}=\frac{A\,e^{-\gamma\,x}-B\,e^{\gamma\,x}}{Z_0}\\<br />Z_{02}\left(x\right)&=&\frac{V\left(x\right)}{I\left(x\right)}=\frac{A\,e^{-\gamma\,x}+B\,e^{\gamma\,x}}{\frac{A\,e^{-\gamma\,x}-B\,e^{\gamma\,x}}{Z_0}}=Z_0\,\frac{A\,e^{-\gamma\,x}+B\,e^{\gamma\,x}}{A\,e^{-\gamma\,x}-B\,e^{\gamma\,x}}\\<br />&=&Z_0\,\frac{1+\frac{B}{A}\,e^{2\,\gamma\,x}}{1-\frac{B}{A}\,e^{2\,\gamma\,x}}\\<br />Z\left(x\right)&=&\frac{Z_{02}\left(x\right)}{Z_0}=\frac{1+\frac{B}{A}\,e^{2\,\gamma\,x}}{1-\frac{B}{A}\,e^{2\,\gamma\,x}}<br />\end{eqnarray}$ 従って既に知っている２つの線路の接合点における反射係数の関係式 $\begin{eqnarray}<br />m_v&=&\frac{Z-1}{1+Z}\\<br />Z&=&\frac{Z_{02}}{Z_{01}}=\frac{1+m_v}{1-m_v}<br />\end{eqnarray}$ を適用するとZ01=Z0でZ02=Z02(x)とした場合と等価なので $\begin{eqnarray}<br />m_v\left(x\right)&=&\frac{B}{A}\,e^{2\,\gamma\,x}\\<br />&=&m_v\left(0\right)\,e^{2\,\gamma\,x}<br />\end{eqnarray}$ ということになる。 γを減衰定数と位相定数で置き換えると $\begin{eqnarray}<br />m_v\left(x\right)&=&m_v\left(0\right)\,e^{2\,\left(\alpha+j\,\beta\right)\,x}=m_v\left(0\right)\,e^{2\,\alpha\,x}\,e^{2\,j\,\beta\,x}\\<br />&=&m_v\left(0\right)\,e^{2\,\alpha\,x}\left(\cos\,2\,\beta\,x+j\,\sin\,2\,\beta\,x\right)<br />\end{eqnarray}$ ということになる。 α＞0の場合には反射係数mv(x)はxが0から増加するにつれ複素平面上の原点の周りを回る拡大螺旋を描くことになる。無損失線路の場合、α＝0であるから反射係数mv(x)は円を描くことがわかる。一方位相定数と波長の関係から $\begin{eqnarray}<br />\beta&=&\frac{2\,\pi}{\lambda}\\<br />m_v\left(x\right)&=&m_v\left(0\right)\,e^{2\,\alpha\,x}\left(\cos\,2\,\frac{2\,\pi}{\lambda}\,x+j\,\sin\,2\,\frac{2\,\pi}{\lambda}\,x\right)\\<br />&=&m_v\left(0\right)\,e^{2\,\alpha\,x}\left(\cos\,2\,\pi\,\frac{x}{\left(\frac{\lambda}{2}\right)}+j\,\sin\,2\,\pi\,\frac{x}{\left(\frac{\lambda}{2}\right)}\right)<br />\end{eqnarray}$ ということになる。すなわち螺旋や円はλ/2単位で一周することになる。 Maximaでmv(0)=1,α=0.01,β=1でプロットしてみると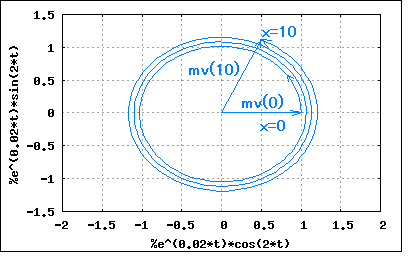ということになる。これの意味するところは、送信端で反射係数が0でないかぎり、送信端から離れるほど反射係数が増大するということである。送信端で多少反射係数が多少なりともあれば、ケーブルが長ければ長いほど受信端での反射係数は増大するということになり、よろしくない結果を招くことになる（受信端に供給される電力が送信端から供給する電力よりも予想外に目減りすることになりかねない）

« 1 2 (3) 4 5 »

スレッド表示 | 新しいものから

前のトピック | 次のトピック | トップ

投稿するにはまず登録を