| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2024-2-7 22:40 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
基本的電荷配位による電界 これまでは点電荷を基本とした電界を考えてきたが、先の電界中に導体が置かれた場合の電界の問題が提起されたことによって、帯電した物体によって生じる電界を考える必要が生じてきた。
実際問題として任意の形状の物体を扱うことは極めて難しいため、簡単に電界が計算できるのは、球、無限に長い円筒、無限に拡がる平面、それぞれ正と負の電荷を帯びた2つの平行平面、の4つについてのみということになる。 (1) 一様に帯電した導体球が作る電界(帯電した総電荷はQとする) 球体表面に一様に電荷が分布して総電荷がQである場合には、これまで学んだ通り、球の中心に総電荷Qの点電荷がある場合と等価な球外の中心からの距離rの電界Eは以下の通り。 ここでnは球体の中心からrの方向へ向かう(球体表面に垂直な)法線ベクトルである。 著者は何故か電界の式をスカラー式として提示しているが、以前に点電荷の作る電界の解説時にはベクトル式として提示していたのととは異なっている。おそらくベクトルとして扱うと話が面倒になるので、スカラー量として扱っていると思われる。単純なケースでは電気力線が直線であることから、電界がベクトルであることは重要ではなくなるためと考えられる。 球外の点の電位Vは、その点から無限遠までの力線に沿った積分になるので、 ということになる。 (2) 表面に一様に帯電した無限長導体円筒(単位長さあたりλの電荷) 長さが無限長なので総電荷も無限大となるため総電荷は不定。 あと、円筒の半径も与えられていないためそれは未知の定数ということになる。 以外と面倒なので図を描く必要があるな。 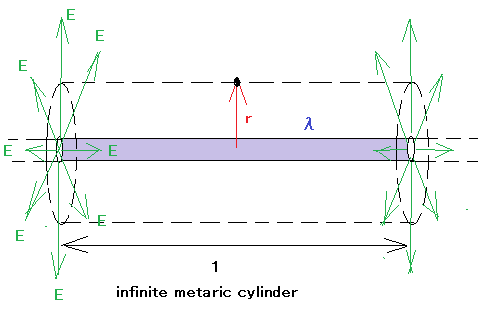 無限に長い導体円筒表面に単位長さあたりλの電荷が分布している場合、電界は円筒表面に垂直な成分のみで円筒の長さ方向の成分はないことになる。 なのでガウスの定理を用いて、円筒の中心から距離rの円筒で囲まれた単位長さの区間について以下が成り立つ。 ということになる。ここでCは無限遠点の電位としての積分定数。 他の参考書では電界強度(En)のみを示して、電位Vには触れないのは、無限遠点での電位とか謎な要素が入ってくるからかな。 (3)一様な面密度σの無限に広い平面状電荷分布 これも電界は平面に垂直な法線方向のみの成分となり、平面に平行な方向の成分は無いとして扱える。 平面状電荷とあるので、線電荷がずらっと密に平面状に並べられたものと考えた方がいい。 図を描いて考えてみよう。 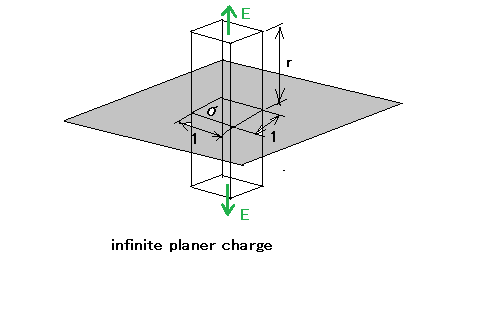 ガウスの定理を使用して下記の関係式が成り立つ。 ということになる。ここでCは無限遠点での電位としての積分定数。 興味深いのは電界強度(E_n)が距離によらず一定であるという点。これはD=ε0Eとあるように、電束密度が変わらないなら電界強度も変わらないため。球電荷の時には電束密度が距離が遠くなれば発散するため無限遠点では0になり、電界強度も0に向かうのとは対照的。 これも電位の式に無限遠点での電位が積分定数として出てくるので、他の参考書では触れないところ。数学的にはこれで合っているけど、現実的ではない。もともと無限長の電荷分布とかが現実的ではないし。 (4)面密度+σ、-σの二つの平行平面状電荷分布 互いに逆の極性だが同じ面密度の2つの平面状電荷分布が平行に置かれているケースを考える。 この場合に難しいのは、2つの平面状電荷分布の間以外は電界が相殺されて無くなるということ。また平面状電荷分布に挟まれた空間では相乗効果で単一の平面状電荷分布の際の2倍の電界強度となる点である。 ややこしいので図を描いて考えよう。 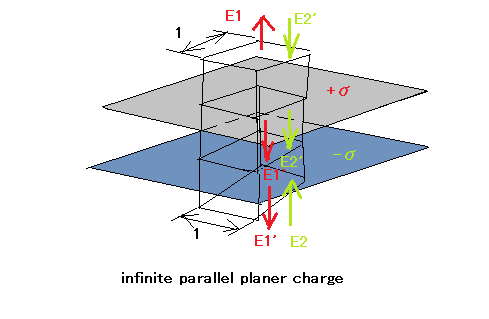 片方の無限平面状電荷分布は+σ、もう片方は-σなので、前者の作り出す平面に垂直な方向の電界をE1,E1'、後者の作り出す電界をE2,E2'とし、ガウスの法則を利用してそれぞれの電界強度を求める。 +σの無限平面状電荷の電界強度に関して、ガウスの法則で以下が成り立つ。 +σの無限平面状電荷の表(上)と裏(下)側で作り出す電界E1,E1'は電界強度は同じだが互いに逆方向を向いているため、以下の関係が成り立つ -σの無限平面状電荷が成す電界強度は同様に以下の通りとなる。 同様に-σの無限平面状電荷が成す電界は表(上)と裏(下)で以下の関係が成り立つ。 従って、2つの無限平面状電荷に挟まれた空間の電界強度は以下の通りとなる。 ということになる。 一方で、平面電荷に挟まれていない空間では以下の通りとなる。 従って参考までに、無限平面状電荷に挟まれた空間の電位は以下のとおり、 ということになる。 ここでCはそれ以外の空間の電位としての積分定数である。 |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| |
webadm | 2024-2-1 19:51 |
| |
webadm | 2024-2-1 23:58 |
| |
webadm | 2024-2-5 16:42 |
| |
webadm | 2024-2-6 7:25 |
| » |
webadm | 2024-2-7 22:40 |
| |
webadm | 2024-2-9 19:41 |
| |
webadm | 2024-2-14 4:27 |
| 投稿するにはまず登録を | |

