| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2024-4-3 18:59 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
続々:直線上の点電荷と電気力線 異符号の電荷、+q, -qが2dだけ離れた点、A, B におかれているとき、ABの垂直二等分線上でABと面との交点Oから距離hの点を通過する電気力線はAからどのような方向に出るか?
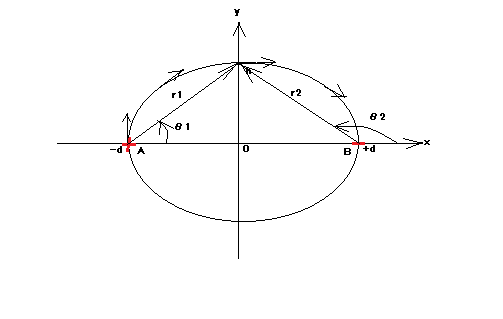 というもの。 これも前問の続きのような問題。今度は具体的に電気力線の形状について問うもの。 前問では電気力線の接線の傾き(微分係数)を導出したが、それを応用できそうである。 (2024.4.5) ふう、また寒くなってきたね( ´д`) さっきまで解答を入力してプレビューしながら内容を確認していたら、突然ブラウザーがエラーページを表示して途中まで編集していた内容が失われた罠(;´Д`) まあ昔からそういうことは時々あったけど、今回は式が途中で複雑になるので、latexのエラーと戦いながらようやく投稿しても良いかなと思える最終確認だったけど、やってしもうた(;´Д`) 再度入力しなおし。 まあ、Maximaの方には式は残っているので、それを元にまたLatexで入力し直せばいいんだけど。作業中の情熱は冷めた罠(;´Д`) なんの話だったっけ? ああ、電気力線の形状の話ね。 失われた作業を思い出して書いてみよう。 幸いにしてサーバーのmathtexのログには、作業中にレンダリングしたLatexテキストがログとして保存されていたのでそれを再利用することにしよう、一番時間がかかったのはそこだから。 前問で電気力線上の座標(x,y)近傍での微分係数が以下の形となることを得た、 これはとどのつまり電気力線の接線の傾き(tan)そのものなので、傾きをθとすると以下の関係が成り立つ。 これだと分母が0になると収束しないので、そうした特異点の無いcosかsinを使用したほうがよさげ。 上のθをcosθに代入して整理すると、 これを見ると一見複雑そうだけど、前問で用いた意図的に1で除するテクニックを使い、点電荷と電気力線上の座標(x,y)を結ぶ線分の長さをr1,r2, 線分とx軸の成す角度をθ1,θ2とすると、 つまるところ、電気力線上の電界のx成分/電界強度ということになる。ファラデーにはこれが見えていたんだろうね、数学的な知識はなくても直感的に電界の姿を電気力線として感じ取ったのは天才のなせる技と納得。 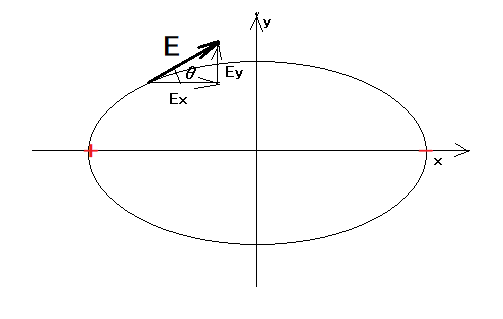 これなら電界強度が無限大になる点電荷のある座標でもcosθ=0となって、電気力線はx軸との垂線方向を向いていることが得られる。 同様に2つの点電荷の中点のy軸上の距離hの座標(0,h)では、題意の条件(点電荷が違いに異極性の場合)Ey=0となることから、|E(0,h)|=Ex となるため、cosθ=1となり、電気力線の向きはx軸に平行となることがわかる。 著者の解答を見ると、上と同じ2点の電気力線の線分の向きを割り出しているが、最後のB点に関しては触れていない。 なぜなら、B点(d, 0)では分子と分母とも0になってしまって値が収束しないため言及を避けたと思われる。 もともと点Aと点Bに関しては上下2つの電気力線の共通の始点と終点であるため、2つの電気力線上の線分の向きのy方向は互いに逆向きなので、近傍といってもどちらも含んでしまう問題がある。 この疑問を解決するのは読者の課題としよう(´∀` ) P.S 後で見直して気付いたんだが、電気力線も電界も、勾配を下る方向が正の向きなんだよな。それで電界成分が+とーで逆じゃね?と思ったんだが元々電位勾配と電界の勾配は符号が逆に定義されているので、間違いではなかったのでした。 |
| フラット表示 | 前のトピック | 次のトピック |
| 投稿するにはまず登録を | |

