| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2024-5-3 22:15 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
帯電した楕円体導体から生じる等電位面 帯電した楕円体導体から生じる電界の等電位面は焦点を同じくする楕円体面になることを示せ。
というもの。 これも数学的でラスボス級だな(´Д`;) だが挑戦してみるテスト まずもって疑問から、 (1) 楕円体って何? 楕円ってなんだっけ? (2) 楕円体の焦点って何? 楕円の焦点は知っているけど。 まずは(1)だけど、立体の断面のどこを切断しても楕円になるのが楕円体ということになる。球も特殊な楕円体ということになる。 特殊な楕円体には球を含め、回転楕円体というのがあり、中心を軸に楕円を回転させてできる立体がそれ。回転楕円体の断面は楕円だったり、円だったりするのはそのため。 特殊でない楕円体はどこで切断しても楕円で円は現れないことになる。 次ぎに(2)だけど、紙の上に楕円を描く簡単な方法として、一定の長さの紐の両端を焦点となる2点にそれぞれ固定し、鉛筆の先端で紐がピンと張った状態を保って焦点を囲む周囲を一周しながら曲線を描くとそれが楕円となるのは良く知られている。 楕円が描いたら、2つの焦点を結ぶ直線を軸に楕円を回転させるとラグビーボール状の回転楕円体(長楕円体)になる。もしくは2つ焦点を結ぶ直線と直交し2つの焦点の中間を通る線を軸といして回転させても球を押しつぶしたような回転楕円体(扁平楕円体)ができる。 因みに地球は完全な球体ではなく、扁平楕円体に近い形状をしているらしい。そのため場所によって重力に差が出る。 さてここで問題になるのが、楕円の焦点は楕円の定義から2つあることが明らかだけど、回転楕円体や一般の楕円体の場合の焦点はどこにあるのかね? 長楕円体の場合は2つの焦点を結ぶ直線を軸対称にしているので焦点の位置は確定するけど、扁平楕円体は焦点が回転するので円状にあることになる? 回転楕円体ではなく一般的な楕円体の場合はどうなる? 楕円に関しては古くからその円周長を求める方法を模索されていたが、18世紀になって微積分の重要な問題となって各種積分法が考案された歴史がある。そのため検索すると楕円の面積とか楕円体の表面積に関する説明ばかりで、それ以前の楕円体とはなんぞや、その焦点とはなんぞやという説明がおろそかになっている。面積や体積を計算する上で必要なのは、楕円の長軸半径と短軸半径だけで争点の位置はそれで決まるので深入りしなくていいということもある。 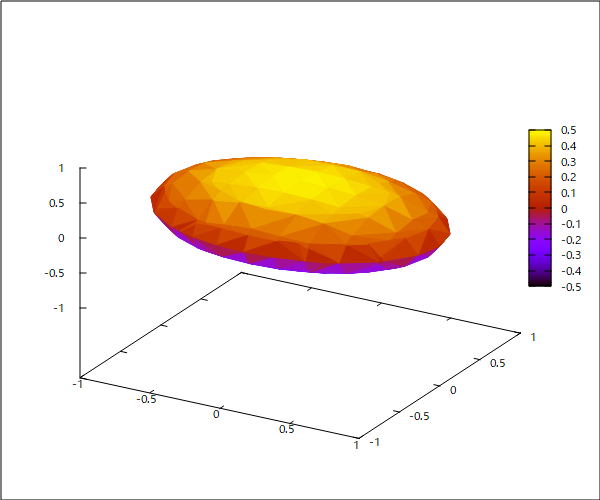 問題文をよくよく読むと、やっぱり焦点は直接関係ないと思われる。平面上の楕円ですら長径と短径で楕円の方程式は定まるので焦点の位置についてはそれと重複する情報となる。 解法のストラテジーとして思いつくのは、 (A) 帯電した楕円体導体が周囲の電荷のない空間に作る電界から等電位面の方程式を導く (B) 上はいきなり三次元なので難しいので、練習として断面が二次元楕円の楕円柱導体に帯電した電荷が周囲の電荷のない平面上に作る電界から等電位面の方程式を導く とりあえず、(B)の手始めとして楕円の方程式を導出してみるテスト。 楕円の定義として終点F1,F2がそれぞれ(-c,0), (c,0)とx座標軸状にあるとして、楕円上の任意の点P(x,y)とF1,F2を結ぶ線分の和が一定値(k)とする。 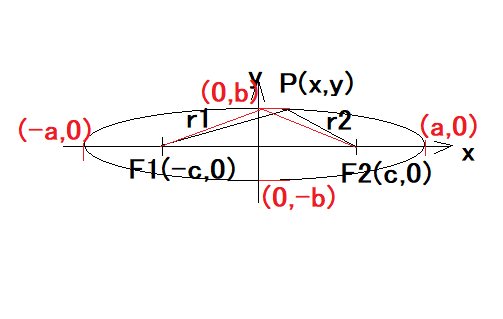 楕円の定義式から根号記号を消すために、式を二乗したり、根号のある単一項を辺の片方にだけに残して更に二乗すると二次の方程式が現れる。長軸と短軸の半径をa,b(a>b>0)とすると、kは長軸の半径の2倍となることから最終的に良くしられた楕円の方程式が導かれる。 楕円線電荷の作る電界を導出するには、楕円の微少線分の法線を知る必要がある。それにはまず楕円の方程式(陰関数表現)から楕円の接線の方程式を陰関数定理を用いて導出すると、 ということになる。 法線は接線と直交するので、以下の関係が成り立つ、 ということになる。 さて問題は法線の方程式は得られたものの、楕円の外の任意の点の電界を導出するには、楕円上の線分に均等に分布した電荷が成す電界を積分する必要がある。 どうすんだこれ(´Д`;) 楕円に沿って積分するには陰関数表現では都合が悪いので、陽関数表現が必要になる。 極座標での楕円の方程式が得られれば、角度を0〜2πまで積分すればいいことになる。 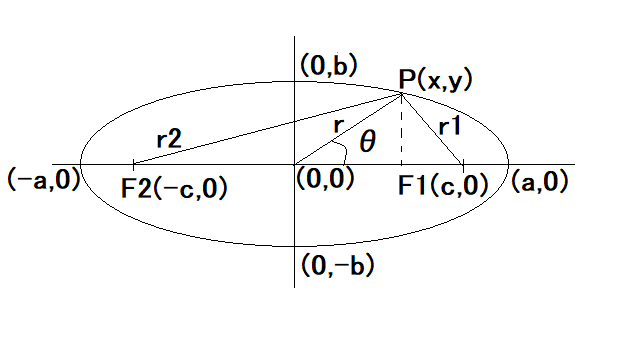 最初式の立て方で単純なミスを犯して、方程式が四次方程式なって解けてもものすごく複雑な解になって心が折れかけたのは内緒だ( ´∀`) ということになる。 焦点cの座標は楕円の長軸半径(a)と短軸半径(b)で決まり任意に設定できるわけではない。 確認のためにmaximaでプロットしてみよう。 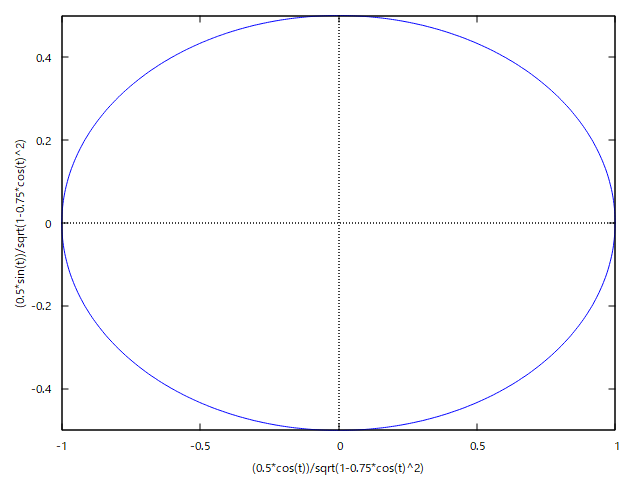 できたじゃないか( ´∀`) 念のために、楕円の方程式のx,yを置き換えてみて成り立つか確認しよう。 ということで方程式を満足することが確認できた。 これであとは、楕円線電荷が作る電界の式を楕円にそって積分して導出すればいいことになる。 しかしMaximaでさくっと積分できると思ったら甘かった(´Д`;) この種の積分は楕円積分と呼ばれ一筋縄では行かないのだった罠(´Д`;) 関係ないが、楕円積分を調べてたら楕円の周長問題のところで、腰が抜けるような楕円の極座標定義を見つけた(´Д`;) いや流石に違うだろうと、先のプロットと重ねてプロットしてみた。 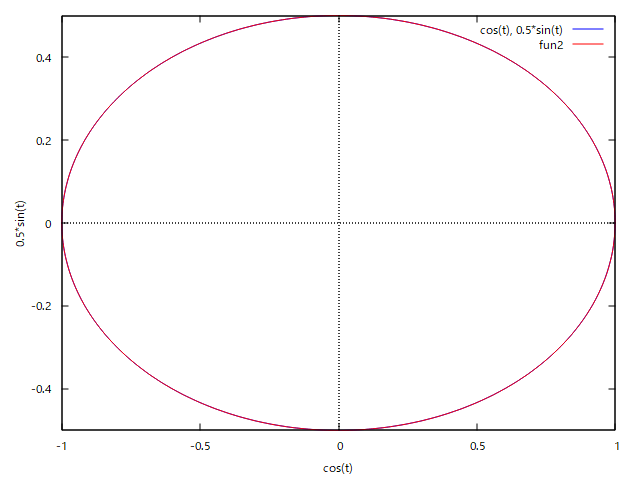 むむ、重なっているとしか見えない、同値だというのか? もはやラマヌジャンの世界だ。 同値かどうか確かめるのは読者の課題としよう(´∀` ) (ヒント:それぞれのθの定義が異なる) いろいろ調べたところ、やはり楕円積分は初等関数(三角関数、根号、べき乗、加減算)では得られず、無限級数の形になることが明らか。 別のアプローチをとらないとだめだな(´Д`;) それと無限長の楕円柱を考えたけど、その場合、電位は無限大になる罠(´Д`;) もともと最初考えたアプローチはだめだめだったことが判明(´Д`;) どうすんだこれ(´Д`;) 著者の解答をチラ見すると、どうやら前問の結果を利用するぽい。前問は等電位面の条件式だったのか? 問題文にそう書いてあった罠(´Д`;) 自分でも記事のタイトルに等電位面としっかり書いてあるし(;´Д`) 全然理解していなかったことがバレバレ。 著者の解答をチラ見しても、字数を減らすためにいろいろ省略している事があるので、そこから紐解いていく必要がある。 まず、最初に疑問に思った楕円体の焦点というのはどういう定義になるのだろうかと。 平面上の楕円に関しては既に焦点(c)もしくは離心率(e)と長軸半径(a)、短軸半径(b)のが一定の関係にあることを明らかにしたので、三次元空間での一般的な楕円体に関して同じ概念が適用できるのか調べてみよう。 楕円体はどの断面を見ても、楕円の方程式を満たす楕円となることから、x-y平面だけではなく、x-zもしくはy-z平面でも同様の方程式が成り立つはずである。 次ぎに疑問だった"焦点を同じくする"という意味はどういうことだろう? 焦点cは、長軸半径(a)と短軸半径(b)と以下の関係がある、 それと異なる長軸半径(a')と短軸半径(b')を持つ楕円が焦点を同じくするためには、以下の関係が成り立つ必要がある。 すなわち異なる2つの楕円が焦点を同じくするためには、それぞれの長軸半径(a,a')のべき乗の差が短軸半径(b,b')のべき乗の差が同じ(λ)である場合ということになる。 焦点を同じくする楕円の離心率(e)は以下の通り、同じではないことに注意する必要がある 以下の2つの楕円方程式は焦点を同じくする これであとは、前問の結果を使って焦点を同じくする楕円体が等電位面であることを示せばよいことになる。 しかし著者はこの問題のネタをどっから仕入れてきたんだろう。検索してもそれらしきものは見つからないので、ネタ元を知っている人はごく限られていると思われる。本当はネタ元を知りたいんだが。 手元にあるWhittaker & Watson本の"18.7 Miscellaneous examples"のExample 18.14(Lamé)に著者の解と同じような楕円体の方程式が出ている。Laméは18世紀のフランスの数学者で、有名な業績としてはn=7でフェルマーが予想した最終定理が正しいことを証明し、完全に証明したと宣言したらしいが問題があることが明らかになりその後同問題からは手を引いた。当時同じ問題に関して同時代の著名な数学者も取り組んでいたらしく、誰も完全証明には至らなかった時代である。 Whittaker & Watson本ではごく短く以下の様に紹介されている。 引用: a,b,c が定数で、λ、μ、νが共焦点楕円体座標(Confocal Ellipsoidal Coordinates)として、元の方程式がεで以下の様に定義されているとして: これはラメが当時高い評価を受けた数理物理の諸問題や弾性問題の中のひとつで、ストレスを受けた楕円体は元の楕円体と焦点を共有するという問題に関連するらしい、どうやら似たような問題を扱っていた数学者らしい。奥が深いな。 19世紀になってJulius Pluckerという数学者がラメにちなんで名付けた、超楕円とも呼ばれるラメ曲線というのがある。 n=2の場合には良く知っている楕円曲線だが、nをそれよりも大きくすると、長方形に近づいていくのが面白い。 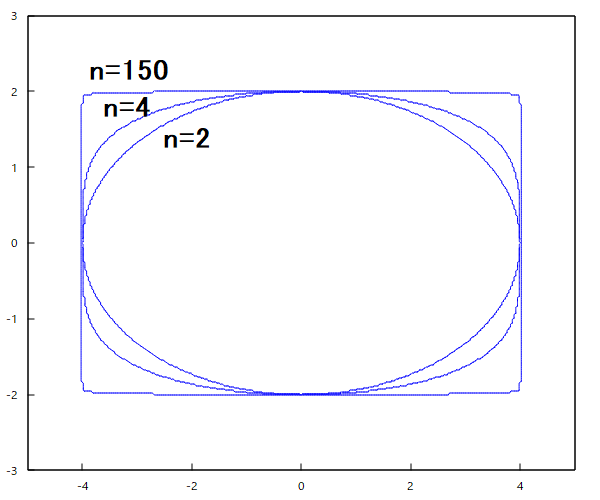 今日のデザイナーはラメ曲線を用いてダイニングテーブルとかをデザインしているらしい。 そういえばあちこちで見かけるのはそういうことだったのか(´∀` ) 欧米の書籍は昔からネタの出典がわかるように書かれているのがありがたいね。それに比べると国内の専門書籍はというと最近はさすがにそうではないけど、ネタの出典はおろか参考書籍すらないという、国内専門書籍あるある、があたり前だったよね。この問題集もそうした時代に書かれたもので、ネタの出所は一切秘密にされている。某有名数学者の解析概論がそうだったからね。みんなそれに習っているのかも。それとも国内の出版社あるある、でページ数を削るために余計なページは省くという方針によるものだったのかも。欧米の書籍はWhittaker & Watson本のように数百ページで単行本というのが普通にあるけど、日本だとある程度ページ数越えると製本が難しいので分冊になるからね。東京空襲の際に帝国大学の図書館が焼けて蔵書していた専門書籍がすべて焼けて無くなったというんもあるだろうけどね。まあ、手元に記録してなければ出典を再度調べるのは億劫だよね。戦後は世界中から失われた専門書を補うべく蔵書が寄付されたぽいね。 なんの話だったっけ? ああ、問題の解答の続きね。 著者の解答はかなり省略が多いので未だに理解できていないのが現状。 先のWHITTAKER & WATSON本に出てきた共焦点楕円体座標(Confocal Ellipsoidal Coordinates)は寺沢本に楕円体のポテンシャル計算に使われるとして楕円座標として紹介されている。 どうやら共焦点楕円体座標というのは元のストレスを受けた楕円体の方程式の膨張もしくは収縮分(λ、WHITTAKER & WATSON本ではε)について解くと、3つの実根が得られるが、それぞれ同じ焦点を共有する楕円体面、一葉総曲面、二葉総曲面に対応する。確かにMaximaで何気なくλについて解いてみたらそれぞれえらく式が複雑で長い3つの根が得られた。そういうことだったのね。 ただ寺沢本では共焦点楕円体座(Confocal Ellipsoidal Coordinates)とよく似た名前の楕円座標(Elliptic coordinate system)が同じものであるとしているが、実際には別物であり、そちらは座標が球座標系での角度であることに注意が必要である。 楕円体座標と称されるものは、共焦点楕円体座標と同意であるが、ラメ以降に近代に至るまで数々の数学者によってバリエーションが複数存在するので寺沢本で紹介されているものだけではないことにも注意が必要である。 (2024/06/09) 著者の解答内容はだいぶ数式処理過程が省略されて誤解しやすい表記もあるので、自分で導出し直してみた。 題意の共焦点楕円体の陰関数定義からλに関する一階と微係数をMaximaで計算してみた。自力でやっても難しくないが、間違いが命とりになるので(実は最初使ったMaximaの簡易GUIアプリ特有のバグがあって、微分した結果の一部しか表示されなくて時間を無駄にしたのは内緒だ)。 ということになる。 一階の微分係数の式を、∂λ/∂xに関して解くと、 ということになる。 同様に∂λ/∂y、∂λ/∂zは、 ということになる。 従って前問の結果で必要な一階の微分係数の二乗和は、 ということになる。 続いて二階の微分の結果を整理してλに関する二階の微分係数に関して解くと、 同様に、y, z軸に関して、 従って二階の微分係数の総和は、 といことになる。 従って前問の条件式は、 となり、λのみの関数であることから等電位面であることが明らか。 この結果を用いて、前問の様に積分して電位の式を導出すると、 ということになる。 ここで境界条件として無限遠点で電位は0となるとすると、積分定数Bは、 ということになる。 積分定数Aに関しては、以前にやった多重極子の様に楕円体中心から楕円体の大きさが無視できる程度十分離れた距離Rから見て楕円体表面に帯電している電荷の成す電界は、帯電している総電荷を持つ点電荷が楕円体中心にある場合に近似できることから、総電荷をQとすると電位は、 ということになる。 著者の解ではだいぶ省略されている導出手順を地道に辿ってみたが、意外性のある事実も判明したりして面白かった(´∀` ) これがこの章の最後の問題だったらいいんだけど、まだラスボス問題が残っているんだな(;´Д`) 良い子は難問に踏みとどまらずに先へ進んで生き延びるように( ´Д`) |
| フラット表示 | 前のトピック | 次のトピック |
| 投稿するにはまず登録を | |

