| ����å�ɽ�� | ��������Τ��� | ���Υȥԥå� | ���Υȥԥå� | ���� |
| ��Ƽ� | ����å� |
|---|---|
| webadm | �������: 2011-9-22 13:23 |
Webmaster   ��Ͽ��: 2004-11-7 �サ��: ���: 3089 |
���ϸ��� �崬�θ�ή��ϩ��������ե��륿�����ޤǤϼ�˼��ȿ��ΰ�Ǥβ�ϩ���Ϥ��濴���ä��������٤ϰ�ž���ƻ����ΰ�Ǥβ�ϩ���Ϥ���Ƨ������뤳�Ȥˤʤ롣
ʣ�Ǽ��ȿ����о줷�Ƥ���ϥ���ԡ����μ��ˤ�äѤ�ʣ�Ǽ��ȿ�s��j�ؤ�������Ѥ��Ƥ����Τϡ����Ԥ�����������������ݤ�¾�η������ѿ���Ʊ�ͤ˵���Ȥ��ư������Ȥ��Ǥ���ʣ�ǿ��Ȥ��Ƥ��㳰�����̹ͤ��ʤ��ƺѤ�Ȥ��������������ä��� ʣ�Ǽ��ȿ���s=��+j�ؤǤ��ꡢ�¿����ϻ����ΰ�Ǥο����λؿ��ؿ�Ū�Ѳ���ɽ�����������ϼ��ȿ�����κ�ɸ���Τǡ���=0�Ȥ�����s=j�ؤȤʤꡢ�������ä������֤η����֤��������������Ȥˤʤ롣����Ϻ��ޤǰ��äƤ���������Ǥ��롣s=0(��=0���Ħ�=0)�Ͼ崬�Ǻǽ�˳ؤ��ľή���ϤȤʤ롣 ���٤���Ϸ����֤����Τʤ�����0�ʦ�=0�ʤ�ľή���ء�0�ʤ��ή�ˤξ������Ȥˤʤ롣 �����������ܤ���٤�ȡ�����Ͼ崬�ǥ���������ȥ���ѥ������ǽ���о줷�����Τ褦�˿��ؤ���ʬ��ʬ��ȤäƲ�ϩ��������ɽ���Ƥ����褦�ˡ������ʤ���ؤ���ʬ��ʬ�������μ������뤳�Ȥ�����Ȥ�����������ˤʤäƤ��롣�¤Ϥ��줬�����餯�ϼ㤤�����ˤȤäƻ����Ȥʤ�����������줬����Ū�ʶ���ˡ�ȤʤäƤ���褦�ʵ������롣 ���Ū�ˤ���ʬ��ʬ�γ�ǰ����Ω����Τ�����Ĺ��ǯ����פ��Ƥ��뤬�����ؤ���ʬ��ʬ����Ȥ��⡢���ؤǤ�������Ѥ���Ȥ��⡢���Ū�ʽ���˽��äƤǤϤʤ��������ʤ���������ڤ�Ф����Ȥ����������ˤʤäƤ��롣�������뤳�Ȥˤ�äƹֵ����֤�����ʬ����ʬ��ʬ�γ�ǰ������Τ���䤵��뤳�Ȥ����뤫���������������Ϥ�äѤ���ּԤ˰Ѥͤ��Ƥ��롣 �긵�Υɥ��Ĥ������ŵ��ؤθ��ܤ�ǽ�λ���������ܿͤǤ�����ٶ����褦�Ȼ�ߤ��褦�ǡ��ǽ����ʬ�ˤ�Ǯ������ǯɮ���ֱ�ɮ�Ǻ٤��ʽ��ߤ����Ƥ��롣�⤷�����ƥɥ��Ĥ���ؤ���������ä���Τ��⤷��ʤ�����������ñ��ľή��ϩ�ȥ���ҥۥåդ�ˡ§�θ�ˤ����ʤ���ʬ������������о줹�뤢���꤫����ߤ��Ѥä���̵���ʤä����ʥڡ����Ф���³���Ƥ��롣������ϥɥ��ĸ�ˤϴ�ǽ���ä��餷����������ʬ���μ��ϳ�̵���ä��ȸ����롣���Υڡ����Ǻ��ޤ����Τ��������ʤ��� ������ʬ�ݤǤ���Ф���˽��������ʤ��ΤǤ��뤬����Ϥ�����ǤϤʤ��Τǡ���������ή���˽���ɬ�פϤʤ��ȹͤ��롣��ʬ��Ǽ���Τ椯�����������Τ����֤Ǥ��롣 �Ȥ������ȤǤޤ����Ƥ��������Ҥä����֤����ǻϤޤ�ΤǤ��뤬�����ϸ��ݤ�ɤ�����ͤ��Ϥ��褤����ʬ��Ǽ���Τ椯�������ȥݥ���Ȥ��������Ȥ���Ϥ��ޤ롣 Ψľ�˸��������ȡ��崬�ǥ���������䥭��ѥ������о줷���Ȥ��Τ��Ȥä���˺��Ƥ��ޤäƤ��롣������ŷ����˶ᤤ�������ǽ̤��Τ������դ��ä��褦������ʬ�ǤϤ�����礳�ʤ���Ǥʤ���ï���������Ǥ��ʤ��ΤǤ��롣�����ϲ��⸫���������ˤ⤿���ˡ����Ĥˤ��餹��Ȥ��ȤλϤޤ꤫�������Ǥ���Τ����ۤ��� ����������Ū�ʥ�������˴ؤ��Ƥ��ܤ��̤�ɬ�פ����롣�ʤˤ�ȴ������Ƥ����ꤷ�ʤ����ɤ����ϥ����å��������� �����Ǥ����Ԥϡ�Valkenburg�Υ�������Ȥ褯������Ω�ƤƤ��롣����Ū�ˤϺǽ�ϰ켡��Ƴ�ؿ���ȼ��������ʬ�������ǰ������ϩ�β��ϸ��ݤ���Ϥ��롣���ˤ���ä����ݤ��ʾ����ʬ������������Laplace�Ѵ���Ƴ��������ΤϤ����DZ黻��ˡ��Ƴ������Ƥ�������������Laplace�Ѵ����֤��������Ƥ���ˡ� ���θ�ˡ��������ä�ʬ�������ϩ�������֡ʼ��ȿ��ΰ���ϡˤȲ��ϸ��ݡʻ����ΰ���ϡˤ��о줹�롣��Τ��ܤˤ�äƤϡ���ü���в�ϩ��������ϩ�ˤ��ä����Ȥ�ʬ�������ϩ���о줹���Τ����롣���������Ĥʤ���Ȥ��ƥ��ࡼ���Ǥ���Ȥ�����롣������ʬ�������ϩ�β��ϲ��Ϥ����Τǰ��̤β�ϩ�β��ϲ��Ϥθ�����餶������ʤ��� ���ؤ���ʬ���������ġ���Ȥ����Ѥ�����Τ���������Ū�ʥ�������ǤϿ��ؤ���ǹ��ؤ����ɤ��ߤ����ʷ����ɤ��Τ��ݤ�ʤ������⤽����ؤǤ���ʬ�������ΰ�������ѿ��ؤȤ�����̣�礤����������ˡ��ǽ�Ū�ʲ��Τν����ؿ��Τɤ�ˤʤ뤫���ꤹ����ˡ��Ʋ���ȻȤ��Ƥ����ꤹ�롣����äȤ��ä��ꤹ�롣������������ˤ��äơ�������碌�����Ƥ��봶�����ݤ�ʤ����ʤ��������뤫��ʹ���Ƥ⡢�ּ������ˤϽ����ؿ���ɽ������Τ���¿��¸�ߤ��뤫��פȤ������Ȥ餷������������Ū�ʲ����Ϥ��äȤФ��Ʒ������������Ѥ��Ƥ���˲�ʤ��� �Ȥϸ�������ʬ�������Τ��ȤλϤޤ�����Ū�ˤ��ɤ�����ѻ��֤��פ���Τǹͤ�ʪ����¿���ο��ؼԤ�Ĺ��ǯ���Фƴؤ�äƤ��뤫���������Ǥ⤽�����θ����̣�Ϥ���ȳο����Ƥ��롣 ��ˤ�Ҥ�Ȥ��С��ŵ���ϩ�β��Ϥ���ʬ���������о줷���Τ��ſ��ȳ��쥱���֥�λ���ˡ�Thomson���ǽ�Ǥ��������ſ����դ��ä�Heaviside�ϥǥ�ޡ����Ǥ��ſ���̳��Ĺ��Υ�ſ�������ï�������Ǥ��ʤ����渽�ݤ��ܤ�������ˤ��Ƥ�������������Ȥ��Ƥ��������θ����줵��Ƥ��ʤ��ä��ż������������줹�뤳�Ȥ���������Maxwell����A Treatise on Electricity and Magnetism�פ���Ǥ���Ƥ��롣Heaviside��16�Фdzع������ष�������ο���Ū���μ�������Ȼ��Ѵؿ����١ˤǤ����������������Ϥ����褦�ȷ�դ�������Ǥ��롣 Thomson�������Ǻǽ�γ��쥱���֥뤬�Ȥ�ʪ�ˤʤ�ʤ���ͳ�Ȥ��ƽ��Ƹ�˳ؤ֤��Ȥˤʤ�ʬ�������ϩ���饤�����������ʬ�����������ϩ��ǥ��ʲ�����ʬ�������Ȥ���ɽ������ �����ʤ�������ʤ��ߤȤ����о줹��Τ������˽��äƤ���ʡ��ϡ����� x�ϥ����֥�ü����ε�Υ��t�ϻ��֤Ǥ��롣������������ȥ����֥�ü����ε�Υx�λ���t�ˤ������Ű�v�μ��������롣K�ϥ����֥��ñ��Ĺ����������͡�C��ñ��Ĺ��������������̤Ǥ��롣�Ĥޤ곤�쥱���֥��������R��C�ε�L����ϩ��̵���˥������³���줿�ե��륿���Ȥ��Ʋ�ϩ��ǥ벽�������Ȥ��̣���롣 ����Ͽ��ؾ�Ǥ�������ʬ�������Ǥ��롣���Ū�ˤϤ����ʤ���֤�������꤬����ä��櫓�Ǥ��롣 Thomson�Ϥ��μ����ɤ��Τ��Ƥ����ΤǤ���Ȥ����Ҥ٤Ƥ��롣�����Fourier�ΰ켡����Ǯ��Ƴ���������쥱���֥���ϩ��Ŭ�Ѥ�����ΤǤ��뤳�Ȥ����餫�Ǥ��롣 Heaviside��Maxwell���ż��������椹����Ǽ��Ȥ��и������ſ���ϩ�����оΤʿ����ư�����Thomson�Υ�ǥ�˹���ͶƳ��ʬ��ñ��Ĺ��������Υ����������s�ˤ��ɲä��뤳�ȤǺ����Τ����ſ��������θ��Ȥ��β��Ū�ʲ�ˡ�ʱ黻��ˡ�ˤ��Ԥ߽Ф����� ����Ϲ������ݤ�����ʬ�������ǡ����������Heaviside��ͭ̾�ʱ黻��ˡ���Ԥ߽Ф������������Ƥ��λ������ŵ���ϩ�β��ϸ��ݤ���Ϥ��뤿��μ�ˡ�����Ǥ˳�Ω�������˸����������ؼԤ���̩���˴ؤ�����Ƚ����ΤȤ�ʢ�˵��ѼԤϼ��餬�����Ƥ��������Τ˱黻��ˡ�����Ѥ��ʤ���Ϥʤ��ä��� Heaviside�α黻��ˡ���ɤ�ʤ�Τ��ä����϶�Ω���ǤΡֿ��ظ�������������פˤ���Heaviside���ڥ졼�����α����㤬¿���ܤäƤ��롣����ʳ�����夹���˽��Ǥ��줿�ŵ���ϩ�������ܤĤ����ɤष���ʤ����ۤȤ�ɸ��߶������Ƥ���Laplace�Ѵ��Ȱ��а���б�����Τ˶ä����⤷��ʤ��� ���ѡ�
��Ω�ο��ظ����ˤ϶���Ū��Laplace�Ѵ������椷�ƾҲ𤵤�Ƥ��� ���ѡ�
�����ܤ���夹���Ի����줿��ΤʤΤ�ɽ���������ˤʤäƤ��餺�ʤ�Τ��Ȥ���äƤ���Τ��������μ�ɮ�Ԥ����糰�������ɤ�Ƚ�äƤ��ʤ��Τ��⤷��ʤ����ŵ��Ǥϵ���ñ�̤Ȥ���j���Ȥ���Τ����̤��������ǤϿ��ؤǤ�i�����ΤޤȤ��Ƥ��롣1(t)��heaviside��step�ؿ��ǡ�t��0��0��t��0��1��Ȥ��ü�ʴؿ��Ǥ��롣��(p)�Ϻ��Ǹ�����ã�ؿ���Laplace�Ѵ�������Τ��������롣p��s���֤�������С����ޤǤ褯�о줷��ʣ�Ǽ��ȿ�����Ѥ�����ή��ϩ�������������ʤ��Laplace�Ѵ����Τ�ΤǤ��롣���ʤߤ�Z(p)�Υ���ԡ����Ȥ����Ѹ������Ѥ����Τ�Heaviside�Ǥ��롣 Laplace�Ѵ��Ǥ����ϴؿ�1(t)��Laplace�Ѵ����ƽ��ϴؿ���Laplace�Ѵ������������ۤʤ뤬������¾��Ʊ���Ǥ��롣 �ȤɤΤĤޤꡢ���ϸ��ݲ��Ϥ�Heaviside�ˤ�ä����˸������������줿��ʬ�������β�ˡ�˵��夹�뤳�Ȥˤʤ롣 ����ʾ���ˤ�é��ȡ�Heaviside���ȳؤ���ã����Ĺ��ƻ�Τ�����θ����뤳�Ȥˤʤ�Τǡ�����Ϥ���äȹ��롣�������Ǻǽ��Thomson������������μ���ͭ���Ƥ��ʤ��ʾ�̵���Ǥ��롣�������줬���Τϰ찮��α��ѿ��ؼԡ������Thomson�䤽�ν�����ͧ��Storkes��������Heaviside���餤�Ǥ��롣 ʬ�����ϩ�����Ǥ��β�ˡ��ؤ֤��Ȥˤʤ롣 ���̤Ϥ�ä�ñ��ʲ�ϩ�Ǥ��ν����뤳�Ȥˤ��褦�� P.S �㤭����Heaviside��̥λ���Ƥ�ޤʤ��ä�Maxwell�Ρ�A Treatise on Electricity and Magnetism�פˤĤ��Ƥ⡢�̤ε���˾ܲ��ż����ر齬�˼���Ȥ�ݤ˸��椹�뤳�Ȥˤ��褦�������ż����ؤ��ܤ�Maxwell���������Ȥ��ƾҲ𤵤�Ƥ����Τϡ����٤��餯Maxwell�Υ��ꥸ�ʥ�Τ�ΤǤϤʤ���Heaviside���٥��ȥ�ݥƥ����������ƴʷ�ǰ����פ�������ΤǤ��뤳�Ȥ��ɤ��Τ��Ƥ��롣Heaviside���Ȥ���ǯ��������Ƥ�äƺƤ�����Maxwell�Υ��ꥸ�ʥ��������ʥݥƥ����ޤࣴ����ɽ���ˤβ��˼���Ȥ�Ǥ����餷���� |
| webadm | �������: 2011-9-24 22:12 |
Webmaster   ��Ͽ��: 2004-11-7 �サ��: ���: 3089 |
���������ϩ�β��ϸ��ݲ��� ��˽Ҥ٤��̤ꡢ���Ū�ˤ�Thomson��Heaviside���Ԥä��褦�˳��쥱���֥��Ĺ��Υ���ſ���ϩ�Τ褦�ʺ����Ǹ���ʬ�������ϩ�β������꤬�����������˺ǽ餫�����Ȥ�ˤϿ���Ū���μ��ν��������ʤ�ɬ�פʤΤǡ������˽��äƸ�ˤ���������ʤ������̤Ϥ������ܻؤ��Τ��Ȥ�������١��������ݤĤ����ˤȤɤ�褦��
����Ū�˲��ϸ��ݲ��ϤϤ���ޤǤⰷ�äƤ������������ϩ�ˤĤ��Ƹ��椹�뤳�Ȥˤʤ롣���������ϩ�Ǥ���л���t�������ѿ��˻��İ��ѿ��ؿ��������Ф褤�Τ����Ū�ϡ��ɥ뤬�㤤�� �ۤȤ�ɤ��ŵ���ϩ�ζ��ʽ���ɼԤ�������ʬ�������β�ˡ���μ���ͭ���뤳�Ȥ�����˲���������ʤ�dy/dt�ʤɤε�����о줵���Ƥ����ʤ���ʬ��������Ҳ𤷤Ƥ��롣�������ٸ��ΤäƤ��Ƥ⤳��������롣 ���⤽����ؤ�����ʬ���ܤǤ���dy/dt�ʳ��ˤ�Ʊ����ǰ�ΰۤʤ�ɽ�����о줹��Τ�Ƭ�����𤹤롣���ä����ɤ��ʤäƤ������ȿ��ؤθ�����䤤�����������Ȥ����Ǥ��뤬���ȶ�˵�ʤ��ΤǼ긵�δ��ȡֿ��ػ�ŵ�פ�Ҥ�Ȥ������ʤ��������ˤ���ʬˡ�ˤĤ��Ƥ��������Ƥ��롣 ���ѡ�
�ʤ���ǽ餫�麮�𤷤Ƥ뤸���ʡ��������� ��ʬ�˴ؤ��Ƥϰʲ��Τ褦�˽�Ƥ��� ���ѡ�
�Ȥ��������Ĥ����餷��������ʴ����Dz��Ǥ⤢�������ʤΤ�Ĺ�����ؤ����Ū�ʻ���ˤ�롣��ʬ���������Ǿ����о줷���Τ�Newton�� ������ؤ�����ʬ�Ǥϸ�̩������¸�ߤ�Ƚ��Ȥ������κ����˴ؤ����ʬ���濴�Ǥ��ꡢ���ѤˤϿ���ʤ����ޤ����Τ������ǰ¿����Ʊ��ѽ����櫓�ǤϤ��뤬�� ���Ʋ����ä����ä����� ���������������ϩ�β��ϸ��ݲ��Ϥ͡� ���������ϩ�β��ϸ��ݲ��Ϥϻ��֤��ѿ��Ȥ���ؿ����Ȥ���쳬�⤷���Ϲⳬ����������ʬ�������������˵��夹�롣����ϸ�ŵ���Ϥλ�����͡��ʲ�ˡ�������Ƥ��ơ����������̤���Ѥ��Ʋ��Ȥ�����롣 �����������Ǥ����Ҳ𤹤�Ȥ����ʤ���ʬ���椬���˸���뤳�Ȥˤʤ�Τǡ�ĩ��٤�������������Ƥ���ɬ�פ����롣 ���⤽�⽸�������ϩ�β��ϸ��ݲ��Ϥ���������Τϲ��ʤΡ� ��ʬ�ζ���ʹ���Ƥߤ뤷���ʤ����������ʤ��Ρ� �����������֤����ϩ���֤��Ѳ��������˰������Ű�����ή���ɤΤ褦���Ѳ����뤫�� ���Ƥ������֤�����夯�Τˤɤ�����λ��֤��פ��뤫�� �Ȥ������Ȥˤʤ롣 �ǽ����ϡ��Ÿ�����³����Ƥ��ʤ���ϩ���Ÿ������(t=0)�ǤĤʤ������˲���Ū�˲�ϩ����ή���Ű����ɤΤ褦���Ѳ�����Τ����狼��ʤ��Ȥ�����̣�ˤʤ롣Ʊ�ͤ˴�����³����Ƥ��ƽ�ʬĹ�����֤��вᤷ�������֤�����夤�Ƥ����ϩ�����Ÿ�������������˲���������Τ���狼��ʤ�������Ū��ȯ�������Ű�����ή����������ǻҤ����줿������������ξ����Ρ���ư��˷Ҥ��뤪���줬���롣�Ÿ������줿�곰���Ƥ�¨�¤˼��������֤��Ѳ�����Τ��Τߤ��������ϩ�����ǡ����ͥ륮�����ߤ��륭��ѥ����䥤���������ޤ��ϩ�ǤϤ����ʤ�ʤ����Ȥ��Ť������Τ��Ƥ��롣�ºݤΤȤ������������ϩ�Ǥ��ϩ���Ű�����ή�Ͻֻ������ꤹ�뤬�����Ϥζ��֤��ż��������Ѥ��뤿��줬�ż��ȡ����ȡˤȤʤäƱ����¤��Ƥ��������Ѥ�⤿�餹�������Ȼפ��ʤ�AM�饸����ʹ���Ƥ�����֤Ǽ¸����Ƥߤ���ɤ�����ϩ���Ÿ���Ĥʤ������ȳ��������˥饸������Υ�����ʹ������Ϥ����� �����ܤϡ������ܤβ���Ū�ʤФ��Ĥ����ɤ줯�餤Ĺ��³���Τ��Τꤿ���Ȥ�����Ρ����̤�����Ȥ��Ǥ�������֤Ȥ�������Ȥ������Ƥ����Τ��������롣 �����������䤬���Ϸ�̤ˤ���ä���뤳�Ȥ���Ū�Ȥ��������ĩ�ळ�Ȥˤ���Х���١�������ݤƤ롣 ��������ǽ������椹�뤳�Ȥˤ��褦��������������Ū�ʥ��ץ������ǤϺǽ�˰���Ū����������ʬ�������β���Τä���ǿʤ��ΤǤϤʤ����������Τ�ʤ��Ȥ�������ǻϤ�뤳�Ȥˤ��롣���ʤ��������ޤdzؤ���褿���Ȱʳ��ο������μ���ڤ����ˤ����̤����դ�ʧ���Ȥ������ȤǤ��롣�����Heaviside�λ���˴����Τ��Ƥ����μ������ǹͤ��Ƥߤ褦�Ȥ������ȤǤ��롣�������ǽ�Ū�ˤϺ����Τ��Ƥ�����ʬ�������β�ˡ�Τɤ줫��Ȥ�ɬ�פ����뤬���ǽ餫�餽�줬���뤳�Ȥ�����ȤϤ��ʤ��Ȥ������ȤǤ��롣����ϲ��Ϥ�ĩ�ि��Υ���١�������⤯�ݤĤ����ɬ�פʤ��ȤǤ��롣������Ƥ����ܤϤ���ޤ�˻����Ǥ��ޤäƤ��롣 ����Ū�ˤ�Valkenburg������ˤ����̤�����꤫��ʤ�Ƥ������Ȥ�����ʤ��Ȼפ���L��R��ľ���ϩ�Ǥ��롣�������������Ǥ϶���Ū������ʬ���μ���ե���Ѥ���ΤǤϤʤ������ޤdzؤ���μ������Dz��Ϥ��뤳�Ȥˤ��롣 ��β�ϩ��LRľ���ϩ�ˣ��Ĥ��Ÿ��ʤҤȤĤ�E���⤦�ҤȤĤ������ʭ�E)��ľ�����³���줿��ϩ�����β�ϩ�Ϻ��ޤdzؤ���Ť�碌������ȤäƲ��ϤǤ������Ǥ��롣���ʤ��E��������³�������˲�ϩ��ή��������֤Ǥ���ή��I�Ȥ�����E��ä���������ή���Ѳ��̤��I�Ȥ���ΤǤ��롣 �����ǭ�E���������֭�t�δ֤��Ѳ����������̤��Ȥ��ơ���I�������֤Ǥϭ�E�����㤹��Ȥ��Ƥ����Ū�ˤ�L�αƶ��ǻ��֤ȶ����Ѳ����뤳�Ȥ�ͽ�ۤ���롣L��ξü���Ű��߲���ή�����ή���Ѳ�®�٤����㤹�뤳�ȤǤ˾崬�dzؤ�Ǥ���Τǡ��ֻ�Ū�ˤϰʲ��δط�������Ω�Ĥ��Ȥˤʤ롣 �ޤ� �Ǥ���ΤǤ������������� �Ȥ������Ȥˤʤ롣������I/��t�˴ؤ������������ ���줫����ήI�λ��֤˴ؤ���ؿ������ˤϤɤ�������ʡ��������� �����ʤ����ƤϤޤä��� Valkenburg���ܤ�ȡ������ˤϡ��ޤ� �֤��� �Ȥ��Ƥ���ξ�դ�e^Pt��褸��� ������Ie^Pt����ʬ��ͤ���� �Ȥ������Ȥˤʤ롣����ϸ�����ʬ�������α��դ�Ʊ�ͤʤΤ� �Ȥ������Ȥˤʤ롣����ʤ�ξ�դ���֤���ʬ����Ф褯 �Ȳ롣���줬��ξ���ʬ�������ΰ��̲�Ǥ��롣 ������t����Ȥ���� �Ȥ������Ȥˤʤ뤳�Ȥ��顢���̲�����ब����ǡ�����ब���֤ȤȤ�˾ü�������ϲ�ȸƤФ���ΤǤ��뤳�Ȥ��狼�롣 �ʤ����ñ����ʤ����ʡ��ϡ����� �Ȥ�����K����ʬ��������������ͤϤɤ���äƷ�ޤ�Τ������� �����Ÿ������äƤ��ʤ����֤���ִ�Ū�˲ä������ˤ�t=0��I=0�ʤ櫓�����顢K=-E/R�Ȥ������Ȥˤʤ롣 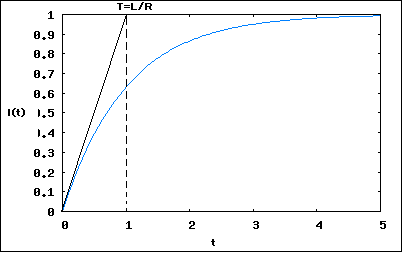 ���٤ϴ����Ÿ�E�����äƤ������(I=E/R)�����Ű���E1�˽ִ�Ū���Ѥ������Ϥɤ���������������(t��0)����ή��E1/R�Ȥʤ�Ϥ��Ǥ��뤫�顢K=E/R-E1/R�Ȥ������Ȥˤʤ롣 ��μ���ꡢE1=0�Ȥʤä������Ÿ��������줿���� �Ȥ������Ȥˤʤ롣  ���ϲ�λؿ����ϻ����T=L/R���������� ��ɽ����롣�����T�Σ��ܤλ��֤��в᤹��Ȥۤ������֤Ȥߤʤ��뤳�Ȥ�t=0��t=5T�λ���e^{t/T}�����������餫�� �ɤ��ܤˤ�Ƥʤ������֤Ǥ��Ÿ�E����ήI���ߤ����Ѳ�ʬ�έ�E��ͤ�����ͳ�ϡ��ɤ��ܤˤ����������˽�Ƥ�����ʬ��������Ω�������´��Τ����Τ��ä�����Ǥ��롣�ǽ�ɤ��˰��´������뤫�狼��ʤ��ä���������ή�Dz��Ϥ��ƤߤƤ�����ͳ���狼�ä��� Newton��Leibniz�λ������ʬˡ���Ѳ��̤�ͭ���ͤ�Ȥꤽ����ʬ��Ϣ³�Ƕ����Ǥ��٤���ʬ��ǽ�Ǥ��뤳�Ȥ�����Ȥ��Ƥ��롣���θ�θ�ŵ���ϤǤ⤳��������Ѥ�äƤ��ʤ���������Ф���Heaviside��ĩ����ſ���ϩ�Ǥ�ľή��ON/OFF�Ȥ�����Ϣ³���������������ʬ������Ǥ������Ǥ���ʬ�Բ�ǽ�ʴؿ���ɬ�פ����ä��������Ǥ�ʤ�ï�⤳�Τ��ȤˤĤ��ƤϿ��줺�˸�ŵ���Ϥ����̤�ή�Ѥ��Ƥ������������Ȱ��´����Ƥ����Τ��ä��� Heaviside���ȼ��ˤ�������˼���Ȥ�������κݤ˳��ʴؿ��ȸƤФ�볬�ʾ��˼�ꤦ���ͤ���������Ķ�ؿ���Ƴ������ɬ�פ����ä��� Heaviside��Ʊ����α��ѿ��ؼ�Bromwich��Heaviside�ȿ�̩�˼�������Ϥ����ʤ��顢Heaviside�α黻��ˡ��Ĵ�²����ǤȤ�������Laplace�Ѵ��Ȥ����Τ���ʣ����ʬ(Bromwich��ʬ�ˤ�¸�ߤ�õ�����Ƥ���Bromwich�Τ�����ʸ�ϴ��˴������Ƥ�������Heaviside�λ��˽��Ǥ����ޤ�ȯɽ����ʤ��ä��ʸ��ߤ⤽����"An introduction to the theory of infinite series."�����Τ���Ƥ���ˡ����κݤ�Heaviside�������˽Ĥ���"Campbridge�ο��ؼԤǤ����ʱ黻��ˡ�Ρ�������������Ǥ��ʤ��Ǥ�����..."�Ȥ������դ�����礤�ˤ��Ƥ�ä������ʸ��ܤ��Ƥ��롣Ʊν�ο��ؼԤ���Heaviside�Ȥζ�Ʊ�����̤Ǥ���ˤ�ؤ�餺���ˤ����Ф����Τ褦�ʤ��Ȥ�ΤϿ�ƻ��ȿ������������������Ӥ�������������Ū���ɤ����ޤ줿Bromwich�ϲ�²�ȻҶ���Ĥ��Ƽ������������������� �ä��ˤ�ɤ����� �ŵ���ϩ���Ÿ���ON/OFF�Τ褦����Ϣ³���Ϥ˴ؤ����ư����Ϥ��뤿��˸�ŵ���Ϥμ�ˡ���٤��٤��Ȥ��Τϴ��ʤä������Ȥ������Ȥ���ͳ��ޤ�Ƥ���Ǥ狼�ä��Ȼפ���t=0�����Ȥ�Ϣ³����ͤ��뤿��ˤ��Ÿ���ON/OFF�Τ褦����Ϣ³�ؿ���Ϣ³�ؿ���̵�¤νŤ�碌��ɽ����Ф褤�櫓�Ǥ��롣��������Ф��줾���Ϣ³�ؿ�����Ÿ����б������ƽŤ�碌�����Dz��ϲ�ǽ�Ǥ��롣������̵�¤ο��νŤ�碌�ҤȤĤҤȤĤˤĤ��Ʋ��Ϥ���ΤǤ�̵�¤λ��֤������롣�ʤΤǸ�ŵ���Ϥ�Ȥ��Τ�����ۤ����褤�Ȥ���������ã���롣����������Ϥ�ͭ�¿���Ϣ³�ؿ��Ǥ���Ф���ɬ�פϤʤ����⤷��ʤ��� ���Ǥ˾崬��Fourier�����Fourier�Ѵ���ؤ��������Ĵ�²��Ϥμ�ˡ���ΤäƤ���櫓�ǡ�����Ǥ���и�ŵ���Ϥ�����Ф����Ȥʤ��ǽ餫��Ĵ�²��Ϥ�Ȥ��Ф褤�ΤǤ��롣�ºݼ긵���ŵ��ز���ǤΡֲ��ϲ�ϩ���ϡפǤϸ�ŵ���ϤϽ��Ϥ����ǡ�����Ϥ���黻��ˡ�ʼºݤˤ�Laplace�Ѵ��ˤ����⤵��ʹߤϤ���Τߤ��Ѥ��Ƥ��롣 �ǽ�˰��´����븶���Ǥ������t=0������Ǥδط��ؿ�����Ϣ³���Ǥ��롣���Τ����ŵ���Ϥμ�ˡ��Ȥ����ˤϡ�t>0�ˤĤ��ƤΤ߹ͤ���ɬ�פ����롣����������ϰ��´������롣ľ��Ū�ˤϻ��ּ����t=0�Ǥ��Ѳ���̵�뤷�Ƥ���ľ��ξ��֤���������Ω�Ƥʤ���йԤ��ʤ�����ï���������Ƥ��ʤ������ؤȸ��äƤ��ޤ��Ф���ޤǤ������⤦�����ޤȤ�ʸ��̤��Τ褤�ͤ����Τ��ʤ��Τ��� ���礦�ɳ��äפ����ؤˤ��ơַ������Ϻ��䤬Ω�äƤ�����֤�����˹Ԥ��ʤ��褦�ˡ������ƺ����Ƥ�������������ͤ���褦�ˡ����ä���ȿ��¦���֤ä���夺���ꤷ�ƤϤ����ʤ��פȶ����Ƥ����ʤ�ޤ����⡢������鷺�˳��äפ��ն��Ĵ�٤�褦�ˤȸ������ï�������鳳���������˷�ޤäƤ���ʡ��ϡ����� (2011/9/25) youTube��MIT��differential Equation�ιֵ��ļ��֤��Ƥ褦�䤯RCľ���ϩ���ä�������äȽФƤ����Ȥ��ˤϤ����������������ޤ�����Τˣ����֤�ιֵ���ɬ�פʤΤ��Ȥ����Τ˶ä����긵�Τɤο��ؤ��ܤˤ�Ƥʤ�����Ū�������μ����֤������Ƥ�����٤ǡ���������������ʤ��Ȥ���ʬ��������ʬ�θ����Τ������Ĥ��ΤäƤ��뤳�Ȥ�����Ȥ������Ȥ��ǧ����ؤ�ʪ���إ������Ȥ��Ǥϡ���ʬ����ʬ�θ������֤��ɥ��Ǵ�����Ƭ�ȼ�˲�����������ˡ��ȤäƤ���Ȥ����⤢��餷������������ʪ���ؼ�Landau�⥻�ߥʡ����ô�˾�γ����ˤϤޤ���ʬ�������Ϳ���ơ�����Τ������������Ƥ����� ����ʤΤ˺���������ʬ�ν�ʪ�����ƤϤ�������롣 ����������������RCľ���ϩ�ˤĤ��Ƥ��ä�����ɤ�������Dz��Ϥ��Ƥߤ褦 RLľ���ϩ�λ��Ȱ�äơ��Ÿ���E(t)�Ȼ��֤δؿ��ˤ��������Τۤ���Ǥ�դν������Ϳ�����롣���Ȥϲ�ϩ��ή�����ή��Ф����櫓���� C��ξü���Ű���C���ߤ���줿�Ų�(��ή�λ�����ʬ�ˤ���������C�dz�ä��ͤ��Ű��ʤΤǡ����줬�ФƤ��롣��R��ξü���Ű��߲���ή�����ήI(t)�����㤹�롣C��R��ξü���Ű��߲��ι�פ��Ÿ�e(t)�Ⱦ�˶ѹդ��Ƥ���Ȥ����������Ƥ��롣 ��ʬ�ब�ޤޤ�Ƥ���Τ���ʬ�������ˤʤäƤ��뤬������ϻ��֤�ξ�դ���ʬ���뤳�Ȥˤ�äư쳬����ʬ�������ˤʤ� �����RLľ���ϩ�λ���Ʊ�ͤ�ɸ�������������� �Ȥ������Ȥˤʤ롣 ������Ʊ�ͤ�integral factor(e^{Pt})��ξ�դ˾褸����������� �Ȥ������Ȥˤʤ롣���Ȥ�ξ�դ���֤���ʬ����Ф褯 �Ȥ������Ȥˤʤ롣 ��ʬ��ʬ�ब�ä��ʤ��ΤǤ������ɤ������餤���Ǥ����ʡ��������� ������� �Ȥ����t��0�ϴ��������֤�I=0�Ǥ���Ȥ���С�������ʬ���ϰϤ�0+(0�����+���ζ�˵�ˤ���t���ϰϤ����Ǥ褤�Τ� �Ȥ������Ȥˤʤ롣 ��ʬ���K���Ĥ�ΤǤ����ɤ�����Ф褤�Ǥ����ʡ��������� t��0�Ǥ������֤Ǥ���Ȥ����Τǡ��Ÿ��Ű���E1���Ѥ�ä��ݤν����ήI0�� �Ȥ������Ȥˤʤ롣���ä�t=0+��I=I0�Ȥ������ʬ���K�� �Ȥ������Ȥˤʤ롣 ���äƤ���β����������� �Ȥ������Ȥˤʤ롣 �㤨��E0=0��E1=1��C=R=1�Ȥ�������I��ץ��åȤ���� 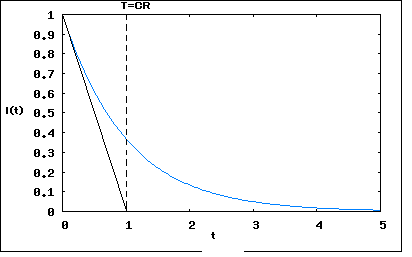 �Ȥ������Ȥˤʤ롣 �դ�E0=1��E1=0�Ȥ������ˤ� 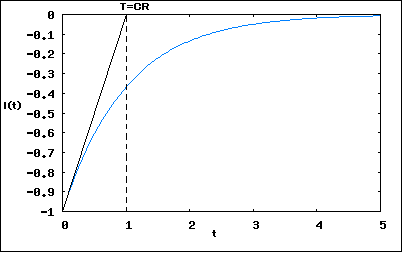 �Ȥ������Ȥ�Ƴ�Ф����ʤ����ݤǥȥ�å��������Ű���ä����ݤȼ��ʧ�ä��ݤΤɤ���β��ޤ�Ǥ������ǤϤɤ��ܤˤ��Ƥ��ʤ������Ǥ��롣 �Ű�E�������ϡ���ήI��®�٤��ɤ��ؤ���ȡ�RLľ���ϩ�ξ����Ƥ֡�RCľ���ϩ�ϥХͤߤ����ʤ�ΤǤ��뤳�Ȥ��狼�롣 ������äƤߤƤ狼��Τϡ����������쳬�ξ���ʬ��ʬ�������Ǥ��äƤ�ΤˤϽ�ʬ�����դ�ʧ��ɬ�פ��Ȥ������Ȥȡ�ʣ���Υ������ҤȤĤβ��ɽ�����ȤϺ���ȼ���Ȥ������ȤǤ��롣����Ū�˰��̲�¸�ߤ����Ȥ��Ƥ⡢��Ū�ν�������������ü���ǽ�Ū������ɬ�פ����롣 �¤Ϥ��Τ褦�ʽ���Ū����ʬ�������β�Ǥϡ�Heaviside��ĩ����褦���ſ���ϩ�β��ϤˤϤϤʤϤ��Խ�ʬ�Ǥ��롣�Ȥ����Τ��������ſ��ϸ��ɸ��Ȥʤä��⡼�륹���Τ褦����ή��ñ�����³�ǤϤʤ���¿�������Ǥ��ä�����������礦�ɸ����Gigabit Ethernet�Τ褦�ˤҤȤĤ�����ϩ��Ϳ�����Ű���٥��ʣ���ʳ��ߤ��ơ����줾��˰ۤʤ뿮����ͤ�⤿���Ƥ����ΤǤ��롣����¦�Ǥϸ�ή�פοˤο�����Ƥɤ��ͤ������Ƥ��Ƥ��뤫�ſ����դ��и�Ū��Ƚ�̤��Ƥ����ΤǤ��롣���줬Heaviside���ȼ��γ��ʴؿ���Ƴ������ɬ�פ����ä���ͳ�Ǥ⤢�롣�ä�������ϩ�Ͻ��������ϩ�ǤϤʤ�ʬ�������ϩ�Ǥ��롣ʬ�������ϩ�β��ϸ��ݲ��Ϥϲ����κǽ��Ϥdzؤ֤��Ȥˤʤ�Ǥ����ʥơ��ޤǤ��롣 ��δ�ñ��RLľ���ϩ��RCľ���ϩ����Ǥ��Ű����Ѳ�ľ���������֤Ȥ��Ƥ������������֤Ǥʤ������Ѳ����������ˤϤ��β�Ȥϰۤʤ��ΤȤʤ롣�ſ�����γ��쥱���֥��Ȥä��̿��Ǥϰ���δֳ֤��֤��ƿ�����Ѳ�������ɬ�פ����ä�����������ο����Ѳ��ˤ����ϸ��ݤ���ʬ���ꤹ�����˼����ο��������Ȳ��ϱ��������蘆�äƼ���¦��Ƚ�̤������������꤬������ˤ���Ǥ��롣���Τ��᳤�쥱���֥��Ĥ��ä��ſ���ʸ�����äƤ���������Τ�¿��ʻ��֤��פ������ɤ���Τˤ�¿��ʻ��֤��פ����Τ��ºݤǤ��롣����Ǥ����Ǽ����Ϥ���Τ����������ä��� ����Ū���Ű��Υ��ƥå��Ѳ������Ǥ��Ѳ������ΰ����ˤĤ��Ƥ��ܤˤ�äƤޤ��ޤ��Ǥ��롣�����ο��ؤǤϴؿ�����Ϣ³����ͭ�¤Ǥ������ʬ��ǽ�Ȥ���Ƥ���Τϡ���Ϣ³���������Ϣ³���ϰϤ���ʬ�����¤��뤳�Ȥ�Cauchy�μ��ͤ�������Ȥ��뤫��Ǥ��롣�����Riemann��ʬ�Ǥ�����Ѥ���Ƥ��롣�������Ѳ������������ʬ����Ȥ������Ȥ��ۤȤ�ɤ��ŵ���ϩ�β��ϲ��Ϥ������ǤϻȤ��Ƥ��롣���������Τ��˹ֵ����֤⾯�ʤ��Ƥ��ष�����ּԤ���ô�⾯�ʤ��ƺѤ�Ȥ������åȤ�⤿�餷����������������ܼ����Ƥ��ޤ��Ȥ���»����⤿�餷�Ƥ��롣 �ɤ��ܤˤ�Ƥ�����ϸ��ݲ��Ϥ���ˡ�Ͼ���ʬ�������β�ˡ���ŵ���ϩ�˱��Ѥ�����ΤǤ��롣���Τ�����Ͽ��ڡ����β�����ɤ������Ǥ����ΤǤϤʤ����������λ��Υɥ��Τ褦�˰פ�����Τ����ʡ�������Τر齬���Ѥ߽ŤͤƤ��ä��ΤdzФ��뤷���ʤ������ϤDz�����ʤ���������ϤDz��Ȥ�ҤȤĤ���ɸ���֤��Τ�����ǡ�����ˤ�ä�Ĺ������١��������ݤĤ��Ȥ�����롣��ͤζ�ϫ�����θ��Ǥ⤢�롣��ˤ���ɴǯ�����Ƥ��ɤäƤ���ƻ���ԥ��ԡ��ɤ����θ����뤳�Ȥˤʤ�Τ�����и礬ɬ�פǤ��롣 �����Ǥɤ����Ƥ����ʬ�������β�ˡ�ˤĤ����η�Ū���μ���������뤳�Ȥ����ʤ�������������ǤϤ��뤬�����̵�����Ʋ��ϸ��ݲ��Ϥ��������Ȥ����Τϡ����ϸ��ݲ��Ϥ��˷�̤����Τꤿ�����ߤ��Ƥ���Τ�Ʊ���Ǥ��롣��ϩ���ߥ�졼�������Ϥ�����������������Ƥ���뤿��ʣ�����ŻҲ�ϩ�ǤϤ������뤳�Ȥ�¿��������̤��ɤ���������������뤫Ƚ�Ǥ���ˤϤ�Ϥ�����ˤ����Ϥ��Բķ�Ǥ������� P.S ���ɤ��ɤ������ϤˤʤäƤ��ޤä�������ɤϾ���ʬ����������Ȥˤʤ롣����Ū�ʲ�ˡ���Ȥ���äȴ��ʤä������Τǡ���äȴ��ؤǴְ㤤�ξ��ʤ���ˡ��Ȥ��Τ�˾�ޤ������������� ���̤�Ǻ�ߤ˲��Ū����ˡ�������Τ�Heaviside�Ǥ��ä����쳬����ʬ���������٤Ǥ���п��ؤΤ����餤�ΤĤ��Ƕ��ʽ�Ū�˲����Ƥ�褤���⤷��ʤ����ⳬ����ʬ�������ˤʤä������Ȥ������Ȥ��Τ��ɤ��������� |
| webadm | �������: 2011-10-10 3:34 |
Webmaster   ��Ͽ��: 2004-11-7 �サ��: ���: 3089 |
����Ū�ʾ���ʬ�������Ȥ��β�ˡ ���Ԥ���Ƭ�Ǥ����ʤ����ʬ������������Ƥ��뤬�������������ͤ����봶������Τ��ݤ�ʤ��������Ǻǽ�����ꤢ�꤭�Ǥ�����Ф��ƿ���Ū�ʸ��Ƥ�Τ�Ŭ���Ǥ���褦�˻פ���
���Ū�ˤ���ʬ������������ʬ�ؤ�Ʊ��������������ΤǤ��뤬������Ū�ˤ�����ʬ�ؤ����ϳ�����ǽŻ뤵�졢��ʬ���������ϸ�����ѿ��ؤȤ��ư����롣�Τ�����ʬ�������β�ˡ�ˤ�����ʬ�ؤ����̤˰�¸���Ƥ���ΤǸ���Ū�˸���й�¤Ū�ˤϤ���Ǥ��äƤ��롣 ��������Ū�Ȥ��������Ǥߤ�ȡ��ǽ����ʬ�������β�ˡ�����ˤ��äơ�����ʬ�ؤ������ȼ�ä�ɬ�פˤʤä��Ȥ��Τ����Ū�ʽ���ˤʤ롣������������ʬ�ؤν�������褯ǧ���Ǥ��롣�������ν��֤�����ʬ�������β�ˡ��������Ǥ�����������ʬ�ؤκ٤������Ƥ�Ƨ�߹��ޤʤ���Фʤ�ʤ��Τǵ����Ȥ��Ƹ��̤��������Ȥ������Ȥϸ����롣 ��ɤɤ����������ʡ��������� �긵�ο��ؤ��ܤƤ�����缣�ֲ��ϳ����פϸ�������ؿ��β��Ϥ���Ȥ��Ƥ���Τǡ���ʬˡ����ʬˡ���о줹�뤬����ʬ���������Ϥޤä������äƤ��ʤ����裷�ϤΡ���ʬˡ��³���ʱ����ؿ��ˡפ������ʬ�������η������äƤ��뤬��ʬ�������Ȥ������ռ��Ȥ������ˤ�̵���� ������Ф��ƹ��ؼԸ����ο��س����Ǥ����������ֿ��س����������ǡˡפˤ��裶�Ϥˡ���ʬ�������ν�����ˡ�פ��о줹�롣�����������ȽƤ��äƤ⡢��ʬ�������β�ˡ�����Ū���͡�����ˡ���о줷�Ƥ��ꡢ¿���Υڡ��������䤫��Ƥ��롣�����ǽ�˳ؤ֤Τ����ѻ��֤��������ͽ�ۤ���롣 ���̤ϼ�ư�ǻҤΤߤ������뽸�������ϩ�β��ϲ��Ϥ������Ф褤�Τǡ���ʬ����������Ǥ�ʲ����ͤ��그��������ʬ�������˸¤äƲ�ˡ�椹��Τǽ�ʬ�Ǥ��롣 x��t����Ω�ѿ��Ȥ���ؿ��ǡ�dx/dt���ѿ�t�˴ؤ���Ƴ�ؿ��Ǥ��롣��ʬ�����������긵���ؿ�x�Ǥ��ꡢ��������Τ���ʬ��������Ȥ�����̣�ˤʤ롣 ����(linear)�Ȥ���̾�����Ĥ��Ƥ���Τϡ����դ��ؿ��Ȥ���Ƴ�ؿ����������ʰ켡���ˤ�ɽ����뤳�Ȥ�ͳ�褹�롣�ŵ���ϩŪ�ǤϤ�������Ť�碌�����Ȥ������Ȥˤʤ롣��������������������ʰ켡�������ˤ��ɤ����Ƥ��롣�����ϼ����Ȱۤʤ뤬����������롣 ���դ�f(t)�Ϻ��դ�Ƴ�ؿ��Ȥ���Ω����Ʊ��t���ѿ��Ȥ���ؿ��� f(t)��0���Ȥ��礦�������������ߤ����ˤʤ�Τǡ���������ñ�ˤʤ롣���������Ʊ��������(linear homogeneous differential equation)�ȸƤФ�롣f(t)��0��������Ʊ��������(linear non-homogeneous differential equation)�ȸƤФ�롣Ʊ���Ȥ������դϸŤ����Ƽ��Ȥ������դ��Ȥ��Ƥ�����������ΰ�̣�˶ᤤƱ�����Ƕ�ǤϻȤ��Ƥ���褦���� �Ȥ����Ǥ��⤽��homogeneous(Ʊ���⤷�����Ƽ�)�äƤʤ�Ǥ����ʡ��������� �ɤ�������Ū�ˤ��ѿ����ܤ��Ƥ��Ѥ��ʤ���Ʊ���ˤȤ�����̣�餷��������Ʊ����ʬ��������ʲ����ͤ˴ؿ�F�Ȥ���ɽ���� �Ȥ�����̣�餷�������ʤ���ѿ���������Ƥ⼰�λ��İ�̣���Ѥ��ʤ���Ʊ���ˤȤ������Ȥˤʤ롣��̤�0�ʤΤ�����������������͡� ���դ�f(t)��0�Ȥʤ���ä��Ϥޤ�ǰ�äƤ��ޤ��� n��0����礭������������n=1�λ�����ʬ�������ȸƤ֡������������ξ��μ���������������ʾ����ʬ��������ͤ�����Τ�Ƴ�ؿ��κǹ⼡���ϳ����Ƥ֤褦������ʬˡ�Ǥ�n����Ƴ�ؿ��ȸƤ�Ǥ���Τ�����ʬ���������Ǥ�n���Ȥ������Ȥˤʤ롣�Ѹ�Ǥϼ�����degree�dz�����order�ȶ��̤���Ƥ��뤳�Ȥ�ͳ�褹�롣����Ȥ��̤���˾����ͳ���鼡���Ǥϣ����ˤ�����(linear)���ˤ�quadratic�������ˤ�cubic�������ˤ�quartic, �����ˤ�quintic�ʤɤȤ�����̾�����롣�����ʾ�������������Ū�˲��Ȥ��Բ�ǽ�ʤΤ�ͭ̾����͡�������first order��������second order�Ȥ�������̡� ���Фλ����ܤǤϺǽ�˰��ִ�ñ�ʰ쳬Ʊ����ʬ����������Ϥ�˽ФƤ���Τϴ��� �����ܤϺǶḫ��MIT����ʬ�������ιֵ���Ʊ�ͤ˰쳬Ʊ����ʬ�������������Ū�ʴ������鸫�뤳�Ȥ���Ϥ��ޤ롣 �Ȥ����쳬Ʊ����ʬ����������ʬ��dy/dx(y�ΰ켡Ƴ�ؿ��ˤ˴ؤ���ʲ��η��˽�ľ�� �����x,y��Ϳ�������ʬ��dy/dx����դ˷�ޤ�ط����Ȥʤ롣��ʬ��dy/dx�ϵ��褦�Ȥ���ؿ�y=F(x)������������ΰ���(x,y)���̤������η������̣���롣 MIT�ιֵ��Ǥϴ�ñ����ʬ����������˼ºݤ˹��ľ��dy/dx����Ʋ�Ȥʤ�ؿ�����ʬ�����Ȥ����⤫�Ӿ夬��Τ��������Ƥ��롣Maxima��plotdf�ѥå�������Ȥ���Ʊ�����Ȥ�����ԥ塼����Ǵ�ñ�˽���롣 ��� �ʤ���ʬ�������ˤĤ���(x,y)�γƳʻ����ˤĤ�����ʬ��dy/dx������Ƥ��η����ȡ��������ܤ��������������Ȥʤ�ؿ�����ʬ�����ˤ������ˤϡ� load("plotdf") plotdf(x+y,[trajectory_at,2,-0.1]) �Ȥ�������Ǥ褤�� (x,y)�γʻ����ϼ¿���Ǥ����̵�¤�¸�ߤ���Τǡ���̵�¤�¸�ߤ��뤳�Ȥˤʤ롣���줬��ʬ�������ΰ��̲�Ǥ��롣����ξ����㤨��ͽ�����줿�����̤�褦�ʶ����ˤ�Ϳ���������������̲���ò�ˤȸƤ֡� ���̲�������ˤϣ��Ĥ��ꡢ�ҤȤĤ�x=0�λ��������y����������̤�������������Ͻ��������(initial condition problem)�ȸƤ֡�Ϳ����줿������������դ˷�ޤ���ˤϤ��β�ˡ���Ȥ��롣 ����ˤ�äƤϡ����������Dz�ʣ��¸�ߤ�����⤢�롣�㤨��x=0,y=y0���̤���ʬ������ʣ������褦�ʾ��Ǥ��롣���ξ��ˤϡ��⤦�����̤�����������̤�褦�ʾ���Ϳ����ɬ�פ����롣�����Σ�������Ȥ��Ʋ�����϶���������(boundary condition problem)�ȸƤФ�롣 �ǽ�˲�LCľ���ϩ��RCľ���ϩ���������ʬ��������Ʊ�ͤ���ʬ���˴ؤ��뼰�˽�ľ���� �Ȥʤ뤫�顢����������t=0,i=1��T=1�Ȥ���plotdf�ǥץ��åȤ��Ƥߤ�ȡ� plotdf(-y,[trajectory_at,0,1],[x,-1,5],[y,-0.1,1]); �Ȥ������˻ؿ��ؿ��������⤫�Ӿ夬�롣 ������Ū�ʻ����������ʬ�������Ϥ������٤ˤ��ơ�����������ˡ�ˤĤ��ƹͤ��Ƥߤ褦�� ���Ф�RLľ���ϩ��RCľ���ϩ����ʬ���������������͡��ʲ�ˡ���Ƥߤ뤳�Ȥˤ��褦�� ���ѿ�ʬΥˡ �쳬Ʊ����ʬ�������ξ��ˤ��ѿ�ʬΥˡ���Ȥ��롣 ������ʬ��������di,dt���̡��ε���Ȥ��ư�����ξ�դ�dt��ݤ���i�dz��� ��ξ�դ�di,dt��ʬΥ�Ǥ��롣�����t=0�ΤȤ�i=i0�Ȥ���ξ�դ���ʬ����� �Ȳ롣 �ǽ�˽������Ϳ��������ʬ�Ǥʤ��Ƥ�������ʬ���뤳�Ȥǰ��̲� �������롣�����ǽ�����t=0,i=i0��Ϳ���뤳�Ȥ� ���ò��Ƴ�����Ȥ�Ǥ��롣 ����ʬ����ˡ�ʤ⤷��������Ѳ�ˡ�� �ѿ�ʬΥˡ���Ȥ��ʤ��褦��������ޤ���ˤ���ʬ����ˡ���Ȥ��롣��ʬ����ˡ����ʬ�������β����ؿ���ɽ�������ˡ������ξ�դ˾褸����ʬ��ǽ���������˽�����ƥ��˥å��Ǥ��롣 �ѿ�ʬΥ������ʤ��ʲ�����������ͤ��� ͽ����ʬ���ҤȤ��ƻ��Ѥ�������ؿ��Ȥ���X(t)��G(t)��ͤ��ʲ��δؿ�����Ȥʤꤨ�뤫Ĵ�٤뤳�Ȥˤ��� �������ʬ����� ���Σ�������������� ������ �Ȳ��ꤹ��� ���ѿ�ʬΥ���Ȥʤ롣 ��ʬ����ȡ� �Ȥ������Ȥˤʤ롣������ꤷ����������������� ����X(t),G(t)�β����μ������������ �����̲�Ȥ������Ȥˤʤ롣 �⤷���ϴ��˼������̤�ˡ���ʬ��������ξ�դ� ��褸��� �ޤ� �Ǥ��뤫�� �Ȥ������Ȥˤʤ롣 ξ�դ���ʬ����Ф褯 ���줬���̲�Ȥʤ롣������Ʊ����ˡ��Ƴ������Τ�Ʊ���Ǥ��롣 ���̤���Ƭ�˸��줿����ʬ�������β�Ϥɤ��ܤˤ�Ƥ����̤�ˡ� �Ȥʤ롣������p1,p2,...,pn�ϰʲ�������������(characteristic equation)�κ��Ǥ��� pj��k�ź��ξ��ˤϡ�Aj���Ȥ����� �Ȥ���Ф褤�� P.S �����ǾҲ𤷤���ʬ�������β�ˡ����������ɮ���줿ë¼����̵���ѹ������ءפͤˤ���������ʬ����ˡ�Ȥ�����ˡ�κǽ�Τ�ΤϤɤ��⺣���Ǥ�����Ѳ�ˡ�ȸƤФ�Ƥ����ΤǤ��롣�ʤˤ⤽��ʸŤ��ܤ�����Ф��ʤ��Ƥ�Ȼפ����⤷��ʤ������Ƕ�Τ�Τ���ʬ�������β�ˡ�˴ؤ���ܤ������⤬�ʤ���Ƥ����Τ��ۤȤ�ɤǤ���Τȡ����ؽ�Ǥ϶����㤬˳�����Ȥ����Τ���ͳ�Ǥ��롣 |
| webadm | �������: 2011-10-10 10:09 |
Webmaster   ��Ͽ��: 2004-11-7 �サ��: ���: 3089 |
RLCľ���ϩ�β��ϸ��ݲ��� ����ޤ��о줷��RLľ���ϩ��RCľ���ϩ�Ϥ������쳬����ʬ�������Ǥ��ä���������n������ʬ�������β�ˤĤ��Ƴؤ���Τǣ�������ʬ�������������RLCľ���ϩ�β��ϸ��ݲ��Ϥ�ĩ��Ȥ��褦��
�긵�Υɥ��Ĥ��ŵ������ζ��ʽ�Ǥϰ��ֺǸ�ξϤ��ż����β��ϸ��ݲ��Ϥ�ҤȤޤȤ�˰��äƤ��롣���λ��˥�ץ饹�Ѵ��ʥ�ץ饹��ʬ�ȥɥ��ĸ�ǤϽƤ���ˤ����Ӳ��⤵��Ƥ��롣�����ꤺ�äȰ����κǽ����������ʬ���ż�����Ϣ�η��Ǥ���Ȥ������о줹�뤬RCľ���ϩ��RLľ���ϩ�Τ褦�ʴ�ñ�ʲ��ϸ��ݲ��ϤäƤ����Τ���ʬ�������β�ˡ�ˤĤ��Ƥβ���ϰ��ڤʤ�����������Ū�β����Ƥ����ޤ��Ȥ��������������ȹⳬ����ʬ�������Σ��Ĥ��㤬�ФƤ��뤬���ⳬ��������˽Ҥ٤�������������Ȥä�ľ�ܰ��̲����Ƥ��롣�ޤ��ŵ���ϩ�β��Ϥ���Ū����ʬ�������β�ˡ��ؤ֤���Ū�ǤϤʤ����餽��Ǥ����Τ��⤷��ʤ��� ���������к�ǯ�ο��إ����ԥå��Ǥϥɥ��Ĥν��ҹ������������������Ȥä��Ȥ�������������������ؼԤ����ޤ줿��������롣 �ä��ˤ�ɤ����� ���RLCľ���ϩ�˴ؤ��ƥ���ҥۥåդ��Ű�§����ʬ�������Ƥ�� �Ȥ������Ȥˤʤ롣 ���������ʬ�ब����Τǡ�ξ�դ�t�˴ؤ�����ʬ����� �Ȥ������Ȥˤʤ롣 �Ȥ����ǡ���������ɤ�����Ф褤�Ǥ����ʡ��������� �ŵ��ز���ŵ����إϥ�ɥ֥å��פˤ�RLCľ���ϩ�β��ϲ��Ϥ��ܤäƤ��뤱�ɡ������ʤ걦�դ�0�ˤʤä�Ʊ�����ˤ��Ʋ��ϲ�����ˤ����Ȥ�����������������Ƥ��ʤ�����Ʊ���ξ�������Ȳ��ϲ���������ˤʤ�Τ��������Τ�����ޤǤϻ��̤��Թ�弨���Ƥ��ʤ������ä����ݤʤΤ��ʡ� ��������Ʋ��ϲ��Ϥ���ʬ�����������Ѹ줬���餬�äƤ��� �Τ��������褦�� ���Ԥ��Ƥ���褦����ʬ�������ΰ��̲��ʪ��Ū�ʴ������鸫��ȡ������֤β�Ǥ�������Ȼ��֤ȤȤ�˾ü�������Ͼ��֤β�Ǥ�����ϲ���¤�ɽ����롣 ����Ū�ˤϡ�����ȸƤФ�Ƥ����Τ��ü�뤤���ò�(particular solution�⤷����particular integral)�����ϲ�ȸƤФ�Ƥ����Τ����(complementary solution�⤷����complementary function)�ȸƤ֤餷���� �ü���ְ�äƲ�ᤷ�Ƥ������Ȥ�ȯ�Сʡ��������� ���Ԥ��Ƥ���褦�ʲ��ϲ��Ϥμ���Valkenburg��Ʊ�ͤΤ��Ȥ�Ƥ��롣�㤦�Τ��Ѹ���������˵��뤫������˵��뤫�ν���ΰ㤤�Τߡ� ����ˤĤ��ƤϺ��ޤǤ�ľή��ϩ���ή��ϩ�Ǥ������֤Ǥβ�ϩ���ϤǤ�ä����Ȥ�Ʊ�������Ȥ�Ʊ����ʬ�������β�Ǥ���������Ƥ�������Ф褤�Ȥ������Ȥˤʤ롣 �ʤ����ñ����ʤ����ʡ��ϡ����� �긵���ŵ���ϩ���ܤ�R.E.SCOTT��LINEAR CIRCUITS�פȤ����ܤ����ꡢ����ϣ�ʬ���ǡ�PART 1/TIME DOMAIN ANALYSIS�פȡ�PART 2/FREQUENCY DOMAIN ANALYSIS�פ������롣���ԤϽ����ľή��ϩ����ϩ���Ϥ���Ϥ��ޤäơ������ΰ�����Dz��ϸ��ݲ��Ϥ�Ԥ��Ȥ���ʬ�����ܤǤ��롣Heaviside���ä����о줹�뤬���黻��ˡ�䤪����Laplace�Ѵ��⤳���ܤˤ��о줷�ʤ�������Ϥɤ��餫�Ȥ�����ʣ�Ǽ��ȿ��ΰ�Ǥβ��ϼ�ˡ�Ǥ��뤫�顢���Ԥμ��ȿ��ΰ���Ϥ��о줹�롣�����ޤ�Ű��Ū�˻����ΰ�����ˤ�����ä����Ƥ�����˭�٤˾Ҳ𤷤Ƥ��뤬���Ǹ�ޤ��ɤ�Τ����ѤǤ��롣�����餯�긵�ˤ����ܤΤʤ��ǰ��֥ڡ�������¿�������Ƥ�˭�٤��� �����ܤǺǽ����ʬ�������β�ˡ���о줹���Ⱦ�ξϤ������۾��Ĺ�������ԤΤ�����꤬�פ�פ�����äƤ��롣����ˤ��ȡ���Ϥ��ŵ���ϩ�Ǥ��그��������ʬ�������Ǥ��Ȥ����Τȡ�����Ϥ����餯��������ʬ����������ǰ���ñ��Ǥ���Ȥ������ȡ���Ʊ����ʬ�������β�������Ʊ���������β�ʲ��ϲ�ˤ��¤Ǥ���Ȥ������ȡ� ���������狼�äƤ����� ���ˤ��Ǥ��그������ʬ�������ΰ��̲�ˤĤ����ΤäƤ���Τǡ������Ȥä����RLCľ���ϩ����ʬ��������Ƥߤ褦�� �ޤ�����ʬ�������Ǥ��뤫�顢��ϰʲ��η���ɽ����뤳�Ȥ��狼�äƤ��롣 �������ʬ���ư켡����Ƴ�ؿ������� �Ȥ������Ȥˤʤ롣�����������ʬ��������Ʊ��������������� �Ȥ������Ȥˤʤ롣 ������A1=A2=0�Ǥ���褦�ʼ����ʾ��������p1,p2�Ϥ������ʲ��������������κ��Ǥ��뤳�Ȥ��狼�롣 �����p�˴ؤ��Ʋ� �Ȥ������Ȥˤʤ롣 �����������������������ʤΤǺ��ϣ��Ĥ��ꡢ���줾��p1,p2�Ȥ������Ȥˤʤ롣 p�μ���褯����ȶ�̣�������¤����餫�ˤʤ롣��0^2��0�Ǥ��뤳�Ȥ���٤����������ͤ����������ͤ�Ķ���뤳�ȤϷ褷�Ƥʤ����������0�Υ������ǤϤ٤�����������Ȥʤ����Ǥ��롣���ʤ��p��ʣ�ǿ��Ȥʤ��0��Ѽ��ȿ��Ȥ��뼫ͳ��ư��ȼ���Ȥ������ȤǤ��롣�����0�ξ���p����μ¿��Ȥʤ꿶ư��ȼ��ʤ��������0�ξ���p�Ͻź�����Ĥ��Ȥˤʤ롣�����Υ������ˤĤ��Ƥϸ�ǵ������褦�� ���ƻĤ�Ϸ���A1,A2�����ɬ�פ����롣������ǵ���Ф����Τ��������긵��A1,A2�ȣ��Ĥ���Τ����̤˹ͤ���н�����⣲��ɬ�פˤʤ롣 �ɤ����������ʡ��������� �ⷬ����Ϻ����ʬ����������ʬˡ�פˤ������˳ؤ����ʬ�������β�ˡ����ǡ�����Ѳ�ˡ��Ȥä�����ʬ��������Ƥ��롣 ����Ѳ�ˡ�Ǥϰ��̲��A1,A2�줾����Ω�����ؿ�A1(t),A2(t)���֤����� ��ɽ�����Ȳ��ꤷ��ʬ����� �Ȥ������Ȥˤʤ롣�������ʬ�������κ��դ���������� �Ȥ������Ȥˤʤ롣 �����Ȥ����ޤ��褿���ɤ��ä���ɤ�������ʡ��������� ����A1,A2������ξ����Ǥ��뤫�顢���ξ�� ������Ω�Ĥ��Ȥˤʤ롣�Ȥ�������μ��� �ȴ�ñ�ˤʤäƤ��ޤ��� ���ä�Ʊ�����������Ʊ�������줾��β�ϰʲ���ϢΩ��ʬ�����������������Ȥˤʤ� �������������ι���ɽ���˽�ľ���� L�ϼ¿���p1,p2����0����μ¿���ʣ�ǿ��Ǥ��뤿�������§�ʲĵաˤǤ���Τǡ����εչ����ξ�դ˾褸��� �Ȥ������Ȥˤʤ롣 ���ä�ξ�դ�t����ʬ�����A1,A2�� �Ȥ������Ȥˤʤ롣 ���ä���Ʊ����ʬ�������β�� �Ȥ������Ȥˤʤ롣 W�Ϧ��ι��ǥ�������(Wronskian)�⤷���ϥ��������ȸƤФ졢��ʬ����� �Ȥ��������������äƤ��뤳�Ȥ����ư�����Ʒ����Ƥߤƽ��Ƥ狼�롣 ����ϰ쳬����ʬ�������ʤΤDz�� �Ȥ������Ȥˤʤ롣 ����������Ʊ����ʬ�������ΰ��̲����������� �Ȥ������Ȥˤʤ롣 �ʤ�̤�ο����������褦�ʡʡ��������� �ǽ����ʬ���椬���룲�Ĥι��t����ˤ��Ƥ�dv/dt��0�Ǥʤ��¤�0�ˤϤʤ�ʤ���������Ǥ��롣�Ĥ����ʬ����������ˤʤä���Τ�p1,p2�μ¿�������Ǥ��뤿��t�����0�Ȥʤ���ϲ�Ȥ������Ȥˤʤ롣����ǰ��̲������Ȳ��ϲ���¤Ǥ��뤳�Ȥ��狼�롣 �Ȥꤢ������Ʊ���������β�Ǥ�v(t)��t=0������ư���ξ�硢t=0������Ƥ�dv/dt=0�Ǥ��뤫���� �Ⱥǽ�˵���ΤȰ��פ��롣ľή�Ÿ��ξ��ˤϥ���ѥ�������ϩ��ľ������äƤ���Τ������0�Ǥ��뤳�Ȥ����餫�� (2011/10/29)�������ɼԤǤ���С����η�̤�t=0�ˤ������ð����λ��ݤȰ��̴ط������뤳�Ȥ˵��Ť������������⤽��ä����Ű����Ѳ���̵�������ή�ˤ��Ѳ��������ʤ�����Ǥ��롣���������ο��ؤǤϤޤ�t=0�λ��ݤ����ʤ�̵���ä��ΤǤȤꤢ�����оݤ���������뤷���ʤ��ä��ΤǤ��롣�����������Ȥ���t=0�λ��ݤ��Τ�ΤϾä���뤳�ȤϤǤ������θ�˱ƶ���ڤܤ��Ƥ���ΤǤ��롣Heaviside�γ��ʴؿ���Dirac�ΦĴؿ��ʤɤ������ο��ؤǤϤ��褽�ؿ��˴ޤޤ�ʤ���ΤǤ��ä����͡�����ͤ����Ϥ��Ѥ߽Ťͤ�Фơ��ǽ�Ū��L.Schwartz������Ū�˴ؿ��γ�ǰ���ĥ��Ķ�ؿ�(distribution)�������Ȥ��ƤޤȤ��ޤǿ���Ū�ʺ���̵�����α��Ѥˤϵ��������;�Ϥ����ä�����ü����Ū�ʺ���Ϳ�������ʪ���ؤ乩�ؤ�ʬ��Ǥ��α��Ѥ����äƤǤ���褦�ˤʤä��櫓�Ǥ��롣��������Ȥ��Ǥ�ɬ���ǽ���о줹��ΤǤ��β��äϷפ��Τ�ʤ����������ŵ���ϩ�����ǤϤޤ������Ȥ鷺�Ȥ��ŵ���Ϥ����ƤǤʤ�Ȥ����ޤ����롣 ���Ʋ��ϲ�����Ū�˵������ˡ�p1,p2�Σ��ĤΥ������ˤĤ��Ƹ��椹��ɬ�פ����롣 �����������β����Ȧ�0��ɽ���������ź�����ľ���R�ξ�P���׳���(critical resistance)Rcr��������褦�� �����׳���Rcr�Ȳ�ϩ��R�������(damping ratio)�Ƥ�������롣 ¾�ˤ�R�ˤ�餺C��L�ˤ�äƷ�ޤ뼫ͳ��ư�Ѽ��ȿ���0������ �������Ѥ��ƺǽ����ʬ��������ɽ���� �Ȥ������Ȥˤʤ롣���ä������������� ��ɽ���줽�κ��� �Ȥ������Ȥˤʤ롣���ä�Ʊ����ʬ�������ΰ��̲�� �Ȥ������Ȥˤʤ롣����Ǥ����ָ��̤����ɤ����ˤʤä��� ����Σ��ĤΥ������� ��������1:�ơ�1�������������κ��ϼ¿� ��������2:�ơ�1�������������κ��ϼ¿��ǽź� ��������3:�ơ�1�������������κ���ʣ�ǿ����Ķ��� ��ʬ��Ǥ��롣 �Ƥ�0�����ޤǼ������Τǡ��ơ�0�ξ���ͤ���������������κ��� �Ƚ�����Ȥʤ롣 �ơ�1�ξ��������������κ���ʣ�ǿ��Ȥʤ�Τǡ��ʲ����ͤ˴����ΤäƤ���Ȥ�����ʣ�Ǽ��ȿ���Ʊ����Τˤʤ� �ޤ�����Ǥ⤢��Τ� �Ȥ����ط�������Ω�ġ� ���äƦơ㣱�ξ��κ��ε��פ�ʣ��ʿ�̾�κ�Ⱦ�̤�Ⱦ�ߤ��������Ȥˤʤ롣 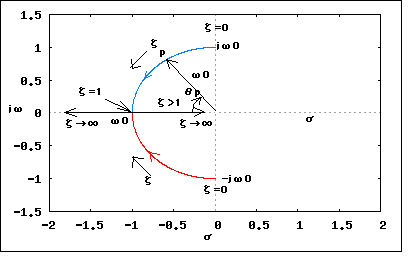 �ޤ�-�Ҥ��Ф����гѤ� �ȦƤΤߤǷ�ޤ롣 ���٤Ϧơᣱ�ξ���ͤ���ȡ���������0�Ȥʤꡢ��μ¼���ΰʲ��ΰ����˽ź�����Ĥ��Ȥˤʤ롣 ���˦ơ�1�ξ��ˤϡ����Ĥκ�����μ¼���ǺƤ���Ω�����줾��Ƥ��礭���ʤ�ˤĤ�ߤ��ո����˵��פ��������Ȥˤʤ� ��^2��1����ٽ�ʬ�礭����硢����-2�Ʀ�0��0�ˤ��줾���Ť����Ȥˤʤ롣 �����ǣ��ĤΥ����������餫�˰ۤʤ���ϲ�ˤĤ��ƾܤ���Ĵ�٤뤳�Ȥˤ��롣 �긵�ˤ���ɤ��ܤ⤳�������褬����ʤΤˤޤ��©�ڤ줷�����Τ褦�ˡ����뤤�ϥڡ������˸¤꤬���뤳�Ȥ˵��Ť��ƽޤ������Τ褦�˸��̤�����뤯�ޤȤޤ꤬�ʤ������ˤʤäƤ��롣 �����ޤǤ�����ʤΤϡ�������ʬ�������ΰ��̲������Ȳ��ϲ�νŤ�碌�Ȥ��ƹͤ��뤳�Ȥ��Ǥ���Ȥ��������Ȥꤢ����Ʊ����ʬ��������Ʋ��ϲ�����в��ϸ��ݲ��Ϥ�Ⱦʬ�Ͻ���ä����Ȥˤʤ롣�Ĥ�������˲ä��������������˴ؤ��ƤϺ��ޤǸ�ή��ϩ�����Ǥ�ä�������Ǥ�����Ϥ��ʤ��ɤ��������������Ӿ�������ɬ�פ�����ˡ� �������ͳ���顢�ǽ餫����ϲ�������濴���������Ƥ����ܤ��Ƕ�Τ�Τ�¿���������ޤ�������㤬���ä��Ȥ��Ƥ���������Ȥ��ƲƤ�������Ǥ��롣��ǽФƤ�������Ѳ�ˡ�Ǥβ�ˡ���Ƥ����ŵ���ϩ�ܤϤۤȤ�ɤʤ�...�Ȼפä��餢�ä��ʡ��ϡ����� ����������äƤ��ʤ����ɼ�����������1��̵�����ѻ��ѡ��ŵ���ϩ�̲����͡פ���13�Ϥˤ�"13.4 R.L.Cľ���ϩ�ξ��"���ꤷ�Ƥ��ʤ�¿���Υڡ�������䤤��Heaviside�����ڥ졼���ʱ黻�ҡˤ�Ȥä���ʬ��������Ƥ�����������Ū�ǤϤʤ���ΤΡ����η�̤�����Ѳ�ˡ�ǵ���Τ�Ʊ����̤�Ƴ���������ܺ٤˵��Ҥ���Ƥ��롣  Ƴ�Фβ�������ǫ�˾�ά���줺�˽�Ƥ���Τǣ��ڡ��������Ф��ơ�1/T1=-p1, 1/T2=-p2���ɤ��ؤ��������Ѳ�ˡ�ǵ�����Ʊ�ͤǤ��뤳�Ȥ��狼�롣  ����ʹߤξϤǤ�Ʊ�ͤ���ʬ��ʬ�����ļ����о줹�롣�黻��ˡ�λ���ǤϤ��줬�����������ä��Τ�������δ�̯����ʬ�������ˤʤ뤬���Ȥꤢ�����ϲ��ϲ�ˤĤ���Ĵ�٤Ƥߤ褦�� (2011/10/29) ���Ƥ�����������ʬ�������˴ؤ��벼Ĵ�٤Ƥ����餢�äȤ����֤˻��֤��ФäƤ��ޤä�������Ϥ���Ǽ��Ϥ������������ä����������κ�����ʬ����������Ƕ���Ǥ��줿������ܤ��ɤ���٤Ƥߤ�ȿ����ʻ����������Ƥ��롣�ä���������λ������鸫���������ʬ�������������Ȼפ�줬���ʥ٥��ȥ���Ϥ�Ʊ����ΤǤ��뤳�Ȥ������Ƥ��롣����˴ؤ��Ƥϥ٥��ȥ���Ϥ������ʤ��о줹���ż�����������ؤֻ��˻פ��Ф����Ȥˤ��褦���ŵ���ϩ�Ǥϸ�ŵŪ�������그����ʬ�����������ƤǤ��Ȥ���뤫����� RLCľ���ϩ�β��ϸ��ݲ��ϤΣ��ĤΥ�������Ǥ�ʷ�˾��ʤ��ڡ������ǤޤȤ�Ƥ���ΤϤ�Ϥ�ɥ��Ĥ��ŵ������ζ��ʽ�Ǥ��롣�����ޤǤε����ˣ��ڡ�������ɬ�פȤ��Ƥ��ʤ����ޤ����̲�μ�������狼������줿�����Ȥ��Ƥ���ʣ������ʬ��Ϻǽ餫��̵��������ˤϤ����ǤΤ����(�ð���t=0����������˰���ޤä��褦�ʵ����ˤ���٤ƴʷ餫�Ĺ�̯�Ǥ��롣�����ޤ���˱齬�������˾Ҳ𤹤뵡����Ȼפ��������ǤϤ��θ�Ⱦ�Σ��ĤΥ������ˤĤ��Ʋ��Ϥ��뤳�Ȥˤ��롣 ��������1:�ơ�1�������������κ��ϼ¿� ���̲�������Ϳ�����ò�������ʳ��Ǥ����ʤ��������ʡ��������� ��Ʊ����ʬ�������ν������������ˤϣ��Ĥ�̤�그��C1,C2���ɬ�פ����롣����ˤϾ��ʤ��Ȥ�C1,C2��ޤࣲ�Ĥ���Ω������������ɬ�פǤ��롣 ������Ȥ���t=+0��i(+0)=0�Ȥ���� �Ȥ������Ȥˤʤ롣��������Ǥ�C1,C2���ʤ��Τ� L��ξü���Ű��߲���u�Ȥ���� �Ǥ��뤫�餷�ơ�������Ȥ���t=+0��u(+0)=v(0)=E0��Ϳ����� ���ä�C1,C2�˴ؤ��Ʋ� �Ȥ������Ȥˤʤ롣 ������Ʊ���������ΰ��̲�μ������������ �Ȥ������Ȥˤʤ롣��˻Ѥ����ʽ�Ũ�ж����ؿ��ʡ��������� ���줬�ɤ�ʶ������������ϺǸ�γڤ��ߤˤȤäƤ����ơ��Ĥ�Υ�������Ĵ�٤褦�� ��������2:�ơ�1�������������κ��ϼ¿��ǽź� n�����������ʬ�������ΰ��̲�������������κ����ź�����ľ��ˤϲ�Ȥ��� �Ȥ������Ȥˤʤ롣����˴�Ť��ƥ���������Ʊ�ͤ˽������Ϳ����C1,C2��� �Ȥ������Ȥˤʤ�C2���������Ф褯 �Ȥ������Ȥˤʤ롣 ���äƲ�� �Ȥ������Ȥˤʤ롣 ����Ȥ��̤˥��������μ��ǦƢ�1�Ȥ��ƶ˸��ͤ���Ƥ�Ʊ����̤������� �Ǥ��뤫�餷�� �Ȥ������Ȥˤʤ롣 �ʤ����ñ����ʤ����ʡ��ϡ����� ���صޤ��� ��������3:�ơ�1�������������κ���ʣ�ǿ����Ķ��� ���������μ���ơ�1�ξ��˰ʲ����ͤ˽����뤳�Ȥ��Ǥ��� ������ �Ǥ��뤫�餷�� �Ȥ������Ȥˤʤ롣 �����ؿ������줿���ɤ���ȷ��ˤʤ뤫�ϼ������������Ĥ��� ����ǤϤ��褤�褳���Σ��ĤΥ��������ȷ���E0=1,L=1,��0=1�ǥץ��åȤ��Ƥߤ褦�� 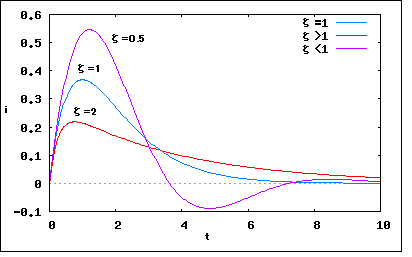 �Ȥ������Ȥˤʤ롣 �ơᣱ�Υ������Ͽ�ư���ʤ��Ǥ�������֤˼�«���롣 �ơ䣱�Υ������Ǥ������֤˼�«����ޤǻ��֤������� �ơ㣱�Υ������Ͽ�ư��ȼ���� �Ǹ�Υ������Ϧ�0���礭���Ƥ�������аʲ����ͤ˿�ư���Ϥä����ǧ�Ǥ��롣 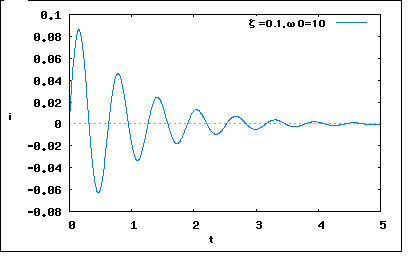 ������Ͽ��ȷ����ɤ����Ƥ��롣 �ơᣱ�Υ��������׳������critical damping) �ơ䣱�Υ�������Ḻ���overdamping) �ơ㣱�Υ�������ưŪ����(oscillatory damping) �ʤɤȼ�ư���������Τɤä��Ƕ���ä����������롣 RCľ���ϩ��RLľ���ϩ�ε�ư�ϰ쳬����ʬ��������ɽ���줿���������ñ���ͥ륮����ϩ�Ǥ���Ȥ������ RLCľ���ϩ�Ǥ�����ʬ��������ɬ�פˤʤ롣�����L��C�Ȥ����줾�쥨�ͥ륮�����ߤ������Ф��֤����Ȥˤ���ͭ���ȿ����ä���ư��ȼ����ǽ�������롢����������ϩ�������ͥ륮����ϩ�ȸƤФ�롣 ���Ƥ���ǰտ��̤���������Ͻ���ä��ΤDZ齬���������� |
| ����å�ɽ�� | ��������Τ��� | ���Υȥԥå� | ���Υȥԥå� | �ȥå� |
| ��Ƥ���ˤϤޤ���Ͽ�� | |

