| スレッド表示 | 古いものから | 前のトピック | 次のトピック | 下へ |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2007-11-11 23:25 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
問題77:温度補償抵抗回路 さてついに直流回路の最後の問題である。がいきなり自分なりに解こうと思ってはまった。
問題は3つの抵抗R1,R2,R3を図の様に接続した回路でR2に流れる電流I2が温度によらず一定になるには3つの抵抗の温度係数α1、α2,α3の関係はどうあらねばならないか導けというもの。 単純に考えるとこの回路全体の合成抵抗の温度係数αが0になるようなα1,α2,α3の関係を導けばいいのではないか。 しかし良く考えたらこれは正しくはない。全体に流れる電流が一定でもR2とR3に流れる電流の配分が変っているかもしれない。そうすると題意とは異なってしまう。 なのでやはり著者と同じようにR2に流れる電流I2に着眼してそれが温度変化にかかわらず一定に補償するためのα1,α2,α3の関係を導く必要がある。 簡単な話I2の式を図のそれぞれの抵抗の温度係数を考慮したものでたてて、それを温度で微分し、得られた微分係数が0となるようなα1,α2,α3の関係を見いだせば良いと思った。 I2=(E*R3*(α3*T+1))/(R2*R3*(α2*T+1)*(α3*T+1)+R1*R3*(α1*T+1)*(α3*T+1)+R1*R2*(α1*T+1)*(α2*T+1)) と表すことができるので、上の式をTで微分すればよい。 (%i75) diff((E*R3*(a3*T+1))/(R2*R3*(a2*T+1)*(a3*T+1)+R1*R3*(a1*T+1)*(a3*T+1)+R1*R2*(a1*T +1)*(a2*T+1)), T); (%o75) (a3*E*R3)/(R2*R3*(a2*T+1)*(a3*T+1)+R1*R3*(a1*T+1)*(a3*T+1)+R1*R2*(a1*T+1)*(a2*T+1))-(E*R3*(a3*T+1)*(a2*R2*R3*(a3*T+1)+a1*R1*R3*(a3*T+1)+a3*R2*R3*(a2*T+1)+a1*R1*R2*(a2*T+1)+a3*R1*R3*(a1*T+1)+a2*R1*R2*(a1*T+1)))/((R2*R3*(a2*T+1)*(a3*T+1)+R1*R3*(a1*T+1)*(a3*T+1)+R1*R2*(a1*T+1)*(a2*T+1))^2 とうことで数学公式の通りのものが出てきた。 問題はTで微分したはずだが微分係数にTが含まれているという点である。 なにか間違っているのだろうか? それぞれの抵抗値は温度によって変化する関数なので数学公式をあてはめても (g(x)/f(x))'=(g'(x)f(x)-g(x)f'(x))/(f(x))^2 ということで分母や分子には元の関数がそのまま現れることになる。 まあそれでも分子が0になる条件を見つければいいのだが、これで同じ結果が出るか謎である。 ちなみに姉妹本の「詳解 電磁気学演習」にもまったく同じ問題が出ているが、著者の解とは異なった表現の答えとなっているが基本的な解法は同じで原始関数である抵抗値R1,R2,R3は温度変化には依存しない定数として扱い、導関数を求める時のみ温度に依存している性質を利用している。 著書の解法は根本的に間違っているような気がするのだが。どうなのだろうか。 ちなみに自分で立てたI2の導関数を整理すると (%i84) factor(%); (%o84) -(E*R3*(a2*a3^2*R2*R3*T^2+a1*a3^2*R1*R3*T^2+a1*a2*a3*R1*R2*T^2+2*a2*a3*R2*R3*T+2*a1*a3*R1*R3*T+2* a1*a2*R1*R2*T+a2*R2*R3+a1*R1*R3-a3*R1*R2+a2*R1*R2+a1*R1*R2))/((a2*a3*R2*R3*T^2+a1*a3*R1*R3*T^2+a1* a2*R1*R2*T^2+a3*R2*R3*T+a2*R2*R3*T+a3*R1*R3*T+a1*R1*R3*T+a2*R1*R2*T+a1*R1*R2*T+R2*R3+R1*R3+R1*R2) ^2 となる。これの分子のTに依存しない要素だけ抜き出すと a2*R2*R3+a1*R1*R3-a3*R1*R2+a2*R1*R2+a1*R1*R2 これが0となるa1,a2,a3の関係を求めると a2*R2*R3+a1*R1*R3-a3*R1*R2+a2*R1*R2+a1*R1*R2=0 両辺をR1*R2*R3で割ると a2/R1+a1/R2-a3/R3+a2/R3+a1/R3=0 整理すると a2/R1+a1/R2+(a1+a2-a3)/R3=0 これは著者の解をR1*R2*R3で割って整理したものと同じである。 問題は自分の式で温度に依存する以下の部分である a2*a3^2*R2*R3*T^2+a1*a3^2*R1*R3*T^2+a1*a2*a3*R1*R2*T^2+2*a2*a3*R2*R3*T+2*a1*a3*R1*R3*T+2*a1*a2*R1*R2*T これも0でなければならないから a2*a3^2*R2*R3*T^2+a1*a3^2*R1*R3*T^2+a1*a2*a3*R1*R2*T^2+2*a2*a3*R2*R3*T+2*a1*a3*R1*R3*T+2*a1*a2*R1*R2*T=0 これを整理すると a3*T^2*(a2*a3*R2*R3+a1*a3*R1*R3+a1*a3*R1*R2)+2*T*(a2*a3*R2*R3+a1*a3*R1*R3+a1*a2*R1*R2)=0 ということになる。従って a2*a3*R2*R3+a1*a3*R1*R3+a1*a2*R1*R2=0 である必要がある。 R1*R2*R3で割ると a2*a3/R1+a1*a3/R2+a1*a2/R3=0 という関係もなりたたないといけないということになる。 これをa3で割ると a2/R1+a1/R2+a1*a2/(a3*R3)=0 これは先の温度に依存しない分子の項から求めた式と部分的に一致しているが最後の a1*a2/(a3*R3)が (a1+a2-a3)/R3とは違っているだけである。 両方の式を満足するには a2/R1+a1/R2+a1*a2/(a3*R3)=a1/R2+(a1+a2-a3)/R3+a2/R1=0 でなければならない すなわち a1*a2/a3=a1+a2-a3 という関係が成り立つ必要がある。 両辺にa3をかけると a1*a2=a1*a3+a2*a3-a3^2 つまり a3^2-a1*a3-a2*a3+a1*a3=0 因数分解できるので (a3-a1)*(a3-a2)=0 という関係が成り立てば良いということになる。 つまりa1=a2=a3なら条件を満たすということか? この考え方はあっているのだろうか? 実際にI2の式にa1=a2=a3としてみたとこで温度項が雲母に残ってしまう。ということでやはり自分の解法はどこか間違っているようだ。 著者の解が正しいかどうかI2の式に代入できる適当な温度係数の値を選ぼうとしてもR1,R2,R3が関係してくるので見つけるのが困難である。やるとするとR1,R2,R3が決まっていて温度係数のうちいずれか一つのみを未知数として関係式から残り1つの温度係数を解くしかないのかもしれない。 実際にやってみよう、R1=1000,R2=2000,R3=3000としてa1=0.01,a2=0.02とした場合に著者の条件を満たすa3を解くと [a3=21/200] という答えが出る。実際にこれらをI2の式に代入してみると (3*E*(21*T+200))/(10*(323*T^2+23100*T+220000)) 全然温度依存している。実際にTを変化させて電流をプロットしてみても 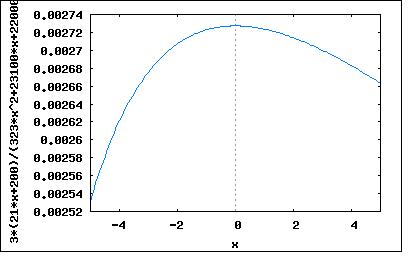 全然補償になっていない。 著者の解は単に一定の温度でI2が最大値を取る温度係数間の関係条件を示しているにすぎない。従って最大値付近では電流の温度変化は確かに少ないが温度によって電流が変化するのは変わらない。 最後の問題で後味を残すことになってしまったが、次ぎの交流回路理論に進むとしよう。 ちなみに温度補償回路はアナログ回路設計ではつきものであるので重要である。極めて短い時間でも回路に流れる電流が増加すれば消費電力が増加しそれが温度上昇を引き起こしそれによって電流が変化するというやっかいな問題が回路が高速になり微少になるにつれ顕在化してくる。 |
| webadm | 投稿日時: 2007-11-11 13:15 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
問題76:導線の温度上昇 あと残すところ2問である。
最後から2つ目の問題は同一の導線にある電圧を印可した際の温度上昇結果からそれとは違う電圧を印可した際の温度上昇を求めよというもの。 これは厳密に考えるとややこしい問題である。導線に一端電流を流すとジュール熱が発生し時間とともに温度が上昇していくことになる。厳密に考えると温度が上昇するに連れ温度係数によって導線の抵抗値も変化し電流もわずかに変化するので時間とともに電流が変化する一種の過渡現象を扱うことになる。また現実には熱は赤外線放射や周囲への熱伝導によって逃げていく熱量と発生する熱量が釣り合わないと永久に温度が上昇し続けることになる。実際に電球のフィラメントの温度が永久に上昇し続ければ電球はすぐに切れてしまう。真空管のヒーターも同様。実際には発生した熱量が周囲に放射したり伝導で奪われることで均衡がとれている。真空の宇宙空間で物体に熱を与え続ければ熱は放射によってのみしか逃げていかないので熱量が多いとすぐ高温になってしまう。これを扱うには10年というか100年早い。 ここでは問題を易しくするために温度上昇は導線に電圧を印可してから十分長い時間(t)経過して発熱と放熱が均衡した時点で測定するものとする。 導線の温度をT1℃上昇させるのに必要なカロリーは導線の半径(r)と長さ(L)それに比熱(c)に密度(d)を使って表すと P1=πr^2LdcT1 この時に導線に印可された電圧(E1)と導線の抵抗(R1)から消費されるt秒間のカロリーは熱による膨張を無視できるとすると P1=0.24I1^2R1t ここでI1は I1=E1/R1 また R1=R(1+αT1) なので P1=0.24(E1/R(1+αT1))^2R(1+αT1)t=0.24E1^2t/R(1+αT1) 従ってどちらのカロリーも等しいので πr^2LdcT1=0.24E1^2t/R(1+αT1) 同様にE2,T2の場合については πr^2LdcT2=0.24E2^2t/R(1+αT2) 二つの式でπr^2Ldcは等しいので整理すると πr^2Ldc=0.24E1^2t/(R(1+αT1)T1)=0.24E2^2t/(R(1+αT2)T2) すなわちπr^2Ldcと共通項を相殺することができ E1^2/(R(1+αT1)T1)-E2^2/(R(1+αT2)T2)=0 が成り立つことになる。 この式をT2についてMaximaで解くと (%i26) solve(E1^2/(R*T1*(a*T1+1))-E2^2/(R*T2*(a*T2+1))=0,T2); (%o26) [T2=-(sqrt(4*a^2*E2^2*T1^2+4*a*E2^2*T1+E1^2)+E1)/(2*a*E1),T2=(sqrt(4*a^2*E2^2*T1^2+4*a*E2^2*T1+E1^2)-E1)/(2*a*E1)] すなわち T2=(sqrt(4αE2^2T1(1+αT1)+E1^2)-E1)/2αE1 ということになり著者と同じ答えが得られたことになる。 著者の解法は前提の説明を省略して温度上昇が消費電力に比例しているという結論から式をたてているが気にいらない。 |
| webadm | 投稿日時: 2007-11-10 11:29 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
問題75:膨張係数と温度係数 今度は抵抗率の温度係数(α)と抵抗の温度係数(α1)を厳密に区別して考える問題。温度膨張係数(β)によって導線が膨張することを考慮した場合の抵抗の温度係数がα-βで近似出来ることを導くもの
著者はいきなり式を近似して導いているが、それとは違った方法で導いてみる。 導線が温度t0での抵抗率をρとした場合の抵抗値(R)は R=ρL/πr^2 で表すことができる。 また温度tでの抵抗値は抵抗率の温度係数(α)と温度膨張率(β)を使って Rt=ρ(1+α(t-t0))L(1+β(t-t0))/(π(r(1+β(t-t0)))^2 と表すことができる。 ここで抵抗の温度係数(α1)を使って温度tでの導線の抵抗値を表すと Rt=R(1+α1(t-t0)) と定義することができる。 従って R(1+α1(t-t0))=ρ(1+α(t-t0))L(1+β(t-t0))/(π(r(1+β(t-t0)))^2 であるので整理すると R(1+α1(t-t0))=(ρL/πr^2)(1+α(t-t0))/(1+β(t-t0)) ここで R=ρL/πr^2 なので R(1+α1(t-t0))=R(1+α(t-t0))/(1+β(t-t0)) この式からα1をMaximaを使って解くと (%i3) solve(R*(1+a1*(t-t0))=R*((a*(t-t0)+1))/((b*(t-t0)+1)),a1); (%o3) [a1=(b-a)/(b*t0-b*t-1)] 分子と分母にそれぞれ-1をかけて整理すると抵抗の温度係数は α1=(α-β)/(1+β(t-t0)) ということになる。 β(t-t0)は1に比べ無視できる程小さい場合 α1≒α-β となるので抵抗値は Rt=R(1+(α-β)(t-t0)) で近似できることになる。 ところで著者の解法で R(1+α(t2-t1))/(1+β(t2-t1)) がいきなり R(1+α(t2-t1))(1-β(t2-t1)) に近似できるというのが未だ理解できない。 おそらくbが1に比べ十分小さい場合 1/(1+b)≒1-b ということで 1/(1+β(t2-t1))≒(1-β(t2-t1)) ということなのだろうけど。これは数学のどこで習うのだろうか? もしかして 1/(1+b)=((1+b)-b)/(1+b)=1-b/(1+b) なのでbが1に比べて十分小さい場合は 1/(1+b)≒1-b ということだろうか。 |
| webadm | 投稿日時: 2007-11-8 14:38 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
Re: 問題74:温度係数 謎が判明した。
姉妹本の「詳解 電磁気学演習」の第5章 定常電流の解説と演習問題がほとんど同じ内容に見えるが実は微妙に違っている。 というのも姉妹本の方では温度係数は電気回路演習の解説とは違って抵抗率の温度係数として説明されている。しかも演習問題も問題74と文章が一部違うだけでほぼ同じものである。 しかし重要な点が違っていた。 電磁気学演習にある電気回路演習の問題74とそっくりの問題の文面はこうである 「抵抗率が温度に対して直線的に増加し、t1℃での温度係数がα1のとき、t2℃での温度係数α2を求めよ。」 それに対して電気回路演習のは 「t1℃のときの温度係数α1なる導線の抵抗値が、温度とともに直線的に増加するとき、t2℃での温度係数α2を求めよ」 明らかに電気回路演習の方は抵抗温度係数として書かれている。 抵抗温度係数はよくTCR(Temperature Coefficient ofResistance)という略語がデータシートとかでは使われる。 |
| webadm | 投稿日時: 2007-11-8 14:07 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
Re: 問題74:温度係数 著者は単に温度係数としているが、検索してみると抵抗率温度係数と抵抗温度係数の2つの定義がある。
抵抗率温度係数は文字通り抵抗率の温度に対する変化率である。 抵抗温度係数が著者の言う温度係数に該当し、抵抗値の温度に対する変化率である。 温度係数の測定に使う式にはまた別のものもあったりして混乱する。 |
| webadm | 投稿日時: 2007-11-8 12:45 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
問題74:温度係数 次ぎの問題も温度係数に関するもの。
導線の抵抗値が温度とともに直線的に増加するものとした場合に温度t1での温度係数α1が与えられて居るときに温度t2での温度係数α2を導けというもの。 ちょっとグラフを書いてみると狐につままれたような感じもしないでもない。温度にともなって直線的に抵抗値が増加するのであればそのカーブは直線になるはず。するとどこでも温度係数は同じじゃないかと思えてしまう。 著者の解法を見るとやはり狐につままれたような感じがする。 グラフの温度係数の関係式から R3=R1*(1+α1*(t3-t1))=R2*(1+α2*(t3-t2)) また R2=R1*(1+α1*(t2-t1)) をR3の式に代入すると R1*(1+α1*(t3-t1))=R1*(1+α1*(t2-t1))*(1+α2*(t3-t2)) R1は共通項なので相殺され (1+α1*(t3-t1))=(1+α1*(t2-t1))*(1+α2*(t3-t2)) 右辺を展開すると 1+α1*(t3-t1)=1+α1*(t2-t1)+α2*(t3-t2)+α1*α2*(t2-t1)*(t3-t2) 両辺の同値を相殺すると α1*(t3-t2)=α2*(t3-t2)+α1*α2*(t2-t1)*(t3-t2) 両辺を(t3-t2)で割ると α1=α2+α1*α2*(t2-t1)=α2*(1+α1*(t2-t1)) 従って α2=α1/(1+α1*(t2-t1)) t2=t1ならα2=α1である。 t2>t1の時に温度係数は低下、t2<t1の時は増加するという意味になる。 やはり狐につままれた感じだ。 |
| webadm | 投稿日時: 2007-11-8 11:40 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
問題73:抵抗値による温度測定 次ぎの問題は温度係数を応用した温度計が可能であることを示す問題。
問題文は導体の抵抗値を測定することによって導体の温度を測定できることを示せとだけある。 予め温度係数がαである温度t0における抵抗値がR0だということがわかっている導体がt1になった時に抵抗値R1へ変化したとするとその時のR1は以下の関係式で近似することができる。 R1=R0*(1+α*(t1-t0)) 従ってt1を求めるには上の式をt1に付いて解けば (%i3) solve(R1=R0*(1+a*(t1-t0)),t1); (%o3) [t1=(R1+(a*t0-1)*R0)/(a*R0)] (%i5) factor(%); (%o5) [t1=(R1+a*t0*R0-R0)/(a*R0)] となり、予め一定の温度(t0)での抵抗値(R0)と温度係数(α)がわかっていれば、現在の抵抗値(R1)を測定すれば現在の温度(t1)を近似的に求めることができる。 著者の解にまたしても誤植があることを発見。 R2の式で説明に出て来ないα1とかいう温度係数が使われているがその後の式でこれはα0の誤植であることが明白である。 |
| webadm | 投稿日時: 2007-11-8 11:20 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
問題72:合成温度係数 次ぎは温度係数を扱う問題。少しひねってある。互いに異なる温度係数α1,α2を持つ抵抗R1,R2を直列に接続した場合、合成された抵抗の温度係数を導けというもの。
まず温度係数の定義を思い出す必要がある。温度係数は微少な温度変化に比例した抵抗値の微少な変化の割合である。 R1とR2を直列に接続した合成抵抗Rtの温度係数をαとすると Rt=(R1+R2)*(1+αΔt) と表すことができる。 一方で合成抵抗はR1,R2それぞれの温度係数α1,α2から Rt=R1*(1+α1*Δt)+R2*(1+α2*Δt) であるので2つの式は等しいことから (R1+R2)*(1+αΔt)=R1*(1+α*Δt)+R2*(1+α*Δt) これをαについて解くと (%i2) solve((R1+R2)*(1+a*t)=R1*(1+a1*t)+R2*(1+a2*t),ro); (%o2) [a=(a2*R2+a1*R1)/(R2+R1)] ということで α=(α2*R2+α1*R1)/(R2+R1) ということで著者の解と同じ結果が得られた。 この式から温度係数がプラスとマイナスの抵抗を直列に接続すればその温度係数が予めわかれば抵抗値を調整すれば合成温度係数を0にすることも可能であるのがわかる。現実には温度係数はすべての温度範囲で一定ではないので広い範囲で温度係数を0とすることはできないが減らすことは可能である。 |
| webadm | 投稿日時: 2007-11-8 11:02 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
問題71:電力量と比熱と融点の応用(フューズ)の続き 次ぎは前の問題の続きである。前問で導体が溶融するまでに要する時間を求める式を導いたが、今度はその時の温度上昇速度を導けというもの。
室温θ0から融点θまで時間tで直線的に上昇するものとみなせば、前の式より (θ-θ0)/t=0.24*I^2*ρ*L/(%pi*r^2)*(%pi*r^2*L*d*c) =0.24*I^2*ρ/(%pi^2*r^4*d*c) ということになる。 |
| webadm | 投稿日時: 2007-11-8 10:54 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
問題70:電力量と比熱と融点の応用(フューズ) 次ぎの問題は熱量に関係するが、更に比熱と融点というのがからんでくる。
半径rの導体に電流Iを流した時に導体が溶けるまでの時間を求めるというもの。フューズの問題だと思った方がぴったりかもしれない。 導体が溶解する温度(融点)まで導体が加熱されるために要する熱量を計算し、1秒当たりの発熱量で割れば溶融までの時間が出るはずである。 溶融する温度はθで与えられている。初期状態の温度を室温θ0と同じにおくと導体をθ-θ0℃だけ上昇させる必要がある。水の場合にはカロリーという簡単な単位があったが、導体の場合はいろいろ金属の種類によって熱し易さが違う。一定の質量の金属を一定温度上昇させるのに要する熱量をその質量と温度で割った値が比熱という単位である。比熱が高ければ同じ質量でも同じ温度まで熱するのに要する熱量を多く必要とすることを意味し、熱し難いと言える。 問題では更に物質の密度dが指定されている。質量を体積で割った値が密度である。これは与えられた半径と長さで示される導体の円柱の体積から質量を求めるのに用いることができる。 導体に流れる電流Iと導体の抵抗がわかれば発熱量がわかる。問題では抵抗値は与えられていないが抵抗率ρが与えられているので同じように導体の断面積と長さから抵抗値を計算することができる。 ここで注意しなければいけないのは比熱は発熱量を質量と温度で割ったものだが、元の発熱量の単位にはジュールとカロリーの2種類がある。そのどちらを扱うかによって計算式は変わってします。著者の解答例を見るとどうやらカロリーを元にしているようである。 そうすると電流と抵抗から計算される熱量はジュールなので式の上では熱量の単位を共通にするための変換を適宜行う必要がある。 まず溶融までに要する時間をtとするとそれまでの間に導体で発生する発熱量Pをカロリー換算で表すと P=0.24*I^2*ρ*L*t/(%pi*r^2) ということになる。0.24は1ジュールに対するカロリーの比である。 次ぎに導体が融点まで達するのに必要な熱量(カロリー)P0は P0=%pi*r^2*L*d*c*(θ-θ0) で表すことができる。 P=P0なので %pi*r^2*L*d*c*(θ-θ0)=0.24*I^2*ρ*L*t/(%pi*r^2) 従って時間tは t=%pi*r^2*L*d*c*(θ-θ0)*(%pi*r^2)/(0.24*I^2*ρ*L) =(4.166666666666667*%pi^2*c*d*r^4*(θ-θ0))/(ρ*I^2) ということになる。Lが相殺されて無関係になっている。 フューズの場合電流値に影響を与えない程度抵抗値が低ければヒューズが切れるまでに要する時間にはフューズ自体の長さに無関係だということだけはわかる。 |
| (1) 2 3 4 ... 13 » | |
| スレッド表示 | 古いものから | 前のトピック | 次のトピック | トップ |
| 投稿するにはまず登録を | |

