Gan's blog - フォーラム

(1) 2 3 4 »

投稿者	スレッド
webadm	投稿日時: 2010-5-2 16:00
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3088	【33】続：定抵抗回路最後の問題。この問題は前問の別バリエーションとも言える。 LとCの直列回路のLとCにそれぞれ抵抗Rを並列接続して周波数によらずインピーダンスが一定となるようにするためのRの条件を示せというもの。この回路は前問でR1,R2を取り除いたもの、すなわちR1=R2=0と置いたものに等しい。前問と同様に駆動点インピーダンス関数の式をたてて解いても良いが、同じことなので、前問の解でR1=R2=0と置けば。 $\begin{eqnarray}<br />\frac{L}{C}&=&R^2\\<br />R&=&\sqrt{\frac{L}{C}}<br />\end{eqnarray}$ という結果が導き出される。これにて一端子対回路の演習問題を終了。長かったよﾏﾏﾝ(ﾉ∀`) 実に半年近く要したことになる。最初温いと思っていたのは大間違いだった。やはりというか、かなり数学の新しい分野とのリンクが多数潜んでいるので、大学の学部で一端子対回路が敬遠される理由がわかる。古い回路網理論の参考書とかでは、実に半分が数学の複素解析のおさらいにページを割いており、現在出版されている回路網理論の本では紹介されていないいくつもの理論や定理が説明されている。それらの理解には数論的代数幾何学の知識が不可欠である。そうした深淵な世界を一端覗いてしまうと代数幾何学にやおら興味が湧いてきた。既に参考書は入手してあるので、いずれ別掲示板で。

webadm	投稿日時: 2010-5-1 9:55
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3088	【32】定抵抗回路長かった一端子対回路の演習問題も残すところあと２つ。最後は定抵抗回路に関する問題のみ。以下の回路が定抵抗回路になる条件を求めよというもの。以前に逆回路の問題で同様の回路を見ている。回路図内のRL直列回路とRC直列回路が互いにRに対して逆回路となれば定抵抗回路となる。従ってRL直列回路のインピーダンスをZ1、RC直列回路のインピーダンスをZ2とすると以下の条件が成り立てば良いことになる。 $Z_1 Z_2=R^2\,\forall\omega$ Z1,Z2はそれぞれ $\begin{eqnarray}<br />Z_1(j\omega)&=&j\omega L+R_1\\<br />Z_2(j\omega)&=&\frac{1}{j\omega C}+R_2<br />\end{eqnarray}$ 従って定抵抗回路となるためには $\begin{eqnarray}<br />Z_1(j\omega)Z_2(j\omega)&=&\left(j\omega L+R_1\right)\left(\frac{1}{j\omega C}+R_2\right)\\<br />&=&R_1 R_2+j\left(\omega L R2-\frac{R1}{\omega C}\right)+\frac{L}{C}\\<br />&=&R^2<br />\end{eqnarray}$ が周波数によらず常に満足すればいいのだが、周波数に依存してしまう、orz... だめだこりゃ(;´Д`) もともと回路がどうみても双対になってないし。逆回路を構成するのは無理ぽ。考え直そう。とりあえず駆動点インピーダンス関数は $\begin{eqnarray}<br />Z(s)&=&\frac{1}{\frac{1}{R}+\frac{1}{L s+R_1}}+\frac{1}{\frac{1}{R}+\frac{1}{\frac{1}{C s}+R_2}}\\<br />&=&\frac{R L\left(s+\frac{R_1}{L}\right)}{L\left(s+\frac{R_1+R}{L}\right)}+\frac{R C R_2\left(s+\frac{1}{C R_2}\right)}{C\left(R+R_2\right)\left(s+\frac{1}{C\left(R+R_2\right)}\right)}\\<br />&=&\frac{R \left(\cancel{L C}\left(R+R_2\right) \left(s+\frac{R_1}{L}\right)\left(s+\frac{1}{C\left(R+R_2\right)}\right)+R_2 \cancel{L C} \left(s+\frac{1}{C R_2}\right)\left(s+\frac{R_1+R}{L}\right)\right) }{\cancel{L C}\left(R+R_2\right) \left(s+\frac{R_1+R}{L}\right)\left(s+\frac{1}{C\left(R+R_2\right)}\right)}\\<br /><br />&=&\frac{R \left(\left(R+R_2\right) \left(s^2+\frac{R_1 C\left(R+R_2\right)+L}{L C\left(R+R_2\right)}s+\frac{R_1}{L C\left(R+R_2\right)}\right)+R_2 \left(s^2+\frac{L+C R_2\left(R_1+R\right)}{L C R_2}s+\frac{R_1+R}{L C R_2}\right)\right) }{\left(R+R_2\right) \left(s+\frac{R_1+R}{L}\right)\left(s+\frac{1}{C\left(R+R_2\right)}\right)}\\<br /><br />&=&\frac{R \left( \left(R+R_2\right)s^2+\frac{R_1 C\left(R+R_2\right)+L}{L C}s+\frac{R_1}{L C}+R_2 s^2+\frac{L+C R_2\left(R_1+R\right)}{L C }s+\frac{R_1+R}{L C}\right) }{\left(R+R_2\right) \left(s+\frac{R_1+R}{L}\right)\left(s+\frac{1}{C\left(R+R_2\right)}\right)}\\<br /><br />&=&\frac{R \left( \left(R+2R_2\right)s^2+\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L}{L C}s+\frac{R+2R_1}{L C}\right) }{\left(R+R_2\right) \left(s+\frac{R_1+R}{L}\right)\left(s+\frac{1}{C\left(R+R_2\right)}\right)}\\<br /><br />&=&\frac{R\left(R+2R_2\right) \left( s^2+\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L}{L C\left(R+2R_2\right)}s+\frac{R+2R_1}{L C\left(R+2R_2\right)}\right) }{\left(R+R_2\right) \left(s+\frac{R_1+R}{L}\right)\left(s+\frac{1}{C\left(R+R_2\right)}\right)}\\<br /><br />&=&\left(\frac{R\left(R+2R_2\right)}{\left(R+R_2\right)}\right)\frac{\left(s+\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L}{2L C\left(R+2R_2\right)}\right)^2-\left(\left(\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L}{2L C\left(R+2R_2\right)}\right)^2-\frac{R+2R_1}{L C\left(R+2R_2\right)}\right)}{ \left(s+\frac{R_1+R}{L}\right)\left(s+\frac{1}{C\left(R+R_2\right)}\right)}\\<br /><br />&=&\left(\frac{R\left(R+2R_2\right)}{\left(R+R_2\right)}\right)\frac{\left(s+\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L}{2L C\left(R+2R_2\right)}\right)^2-\left(\sqrt{\left(\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L}{2L C\left(R+2R_2\right)}\right)^2-\frac{R+2R_1}{L C\left(R+2R_2\right)}}\right)^2}{ \left(s+\frac{R_1+R}{L}\right)\left(s+\frac{1}{C\left(R+R_2\right)}\right)}\\<br /><br />&=&\left(\frac{R\left(R+2R_2\right)}{\left(R+R_2\right)}\right)\frac{\left(s+\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L}{2L C\left(R+2R_2\right)}-\sqrt{\left(\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L}{2L C\left(R+2R_2\right)}\right)^2-\frac{R+2R_1}{L C\left(R+2R_2\right)}}\right)\left(s+\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L}{2L C\left(R+2R_2\right)}+\sqrt{\left(\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L}{2L C\left(R+2R_2\right)}\right)^2-\frac{R+2R_1}{L C\left(R+2R_2\right)}}\right)}{ \left(s+\frac{R_1+R}{L}\right)\left(s+\frac{1}{C\left(R+R_2\right)}\right)}\\<br /><br />&=&\left(\frac{R\left(R+2R_2\right)}{\left(R+R_2\right)}\right)\frac{\left(s+\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L-\sqrt{\left(C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L\right)^2-4\left(R+2R_1\right)\left(L C\left(R+2R_2\right)\right)}}{2L C\left(R+2R_2\right)}\right)\left(s+\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L+\sqrt{\left(C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L\right)^2-4\left(R+2R_1\right)\left(L C\left(R+2R_2\right)\right)}}{2L C\left(R+2R_2\right)}\right)}{ \left(s+\frac{R_1+R}{L}\right)\left(s+\frac{1}{C\left(R+R_2\right)}\right)}\\<br /><br />&=&H\frac{\left(s+s_1\right)\left(s+s_3\right)}{ \left(s+s_2\right)\left(s+s_4\right)}\\<br /><br />&=&H\frac{s^2+\left(s_1+s_3\right)s+s_1 s_3}{ s^2+\left(s_2+s_4\right)s+s_2 s_4}\\<br /><br />H&=&\frac{R\left(R+2R_2\right)}{\left(R+R_2\right)}\\<br />s_1&=&\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L-\sqrt{\left(C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L\right)^2-4\left(R+2R_1\right)\left(L C\left(R+2R_2\right)\right)}}{2L C\left(R+2R_2\right)}\\<br />s_3&=&\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L+\sqrt{\left(C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L\right)^2-4\left(R+2R_1\right)\left(L C\left(R+2R_2\right)\right)}}{2L C\left(R+2R_2\right)}\\<br />s_2&=&\frac{R_1+R}{L}\\<br />s_4&=&\frac{1}{C\left(R+R_2\right)}<br /><br />\end{eqnarray}$ ということになり、s1,s3に零点をs2,s4に極を持つ。既に定抵抗回路の理論で学んだ通り、またLiouvilleの定理にあるようにすべてのsに対して正則で零点も極ももたない関数は唯一定数であるので、以下の様に零点s1,s3と極s2,s4が互いに相殺し合って消失しなければならないことになる。 $\begin{eqnarray}<br />Z(s)&=&H\frac{\left(s+s_1\right)\left(s+s_3\right)}{ \left(s+s_2\right)\left(s+s_4\right)}\\<br />&=&H\frac{s^2+\left(s_1+s_3\right)s+s_1 s_3}{ s^2+\left(s_2+s_4\right)s+s_2 s_4}\\<br />&=&H\,\,\forall s<br />\end{eqnarray}$ 上記の様に零点と極が互いに相殺し合う条件は、s1=s2かつs3=s4もしくはs1=s4かつs3=s2が成り立つ時で、その場合以下も成り立つことになる $\begin{eqnarray}<br />\frac{s_1+s_3}{s_2+s_4}&=&\frac{s_1 s_3}{s_2 s_4}=1<br />\end{eqnarray}$ s1,s2,s3,s4をそれぞれ代入してみると $\begin{eqnarray}<br />\frac{\left(R_2+R\right)\left(C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L\right)}{\left(2R_2+R\right)\left(C\left(R+R_1\right)\left(R+R_2\right)+L\right)}&=&\frac{\left( 2R1+R\right)\left( R2+R\right) }{\left( R1+R\right)\left( 2R2+R\right) }=1\\<br />\frac{C\left(R\left(R_1+R_2\right)+2R_1 R_2\right)+2L}{C\left(R+R_1\right)\left(R+R_2\right)+L}&=&\frac{\left( 2R1+R\right)}{\left( R1+R\right) }=\frac{\left(2R_2+R\right)}{\left(R_2+R\right)\\<br />\end{eqnarray}$ 従って少なくとも $R_1=R_2$ でなければならない。上記の関係を更に代入すると $\begin{eqnarray}<br />\frac{2C R_2\left(R+R_2\right)+2L}{C\left(R+R_2\right)^2+L}&=&\frac{\left(R+2R_2\right)}{\left(R+R_2\right) }\\<br /><br />\frac{2C R_2\left(R+R_2\right)^2+2L\left( R+R_2\right)}{C\left(R+R_2\right)^2\left(R+2R_2\right)+L\left(R+2R_2\right)}&=&1\\<br /><br />2C R_2\left(R+R_2\right)^2+2L\left( R+R_2\right)&=&C\left(R+R_2\right)^2\left(R+2R_2\right)+L\left(R+2R_2\right)\\<br /><br />L&=&C\left(R+R_2\right)^2\\<br /><br />\frac{L}{C}&=&\left(R+R_2\right)^2=\left(R+R_1\right)^2<br /><br />\end{eqnarray}$ という必要十分条件が導き出される。これも一種の不定方程式を解く問題である。これらのことから、回路網理論は数学の代数幾何学と表裏一体であることが判る。いずれ別の機会に代数幾何学を独学したいと思う。この分野に関しては戦後になって日本人数学者がめざましい貢献をしていたのだが工学における重要性が理解されるず、他の先進国に先取りされてしまった感がある。最先端のEDAツールや信号処理や検索エンジンではそれぞれ特有の不定方程式の解を有限時間で求めるためのアルゴリズム開発に数論的代数幾何学の知識が不可欠だからだ。

webadm	投稿日時: 2010-4-30 12:03
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3088	【31】もうひとつの：逆回路これが最後か逆回路の問題。最後はLattice回路のご登場。この次に学ぶ二端子対回路で本格的に学ぶことになる。 Z1とZ2がRに対して逆回路である場合、定抵抗回路になることを示せというもの。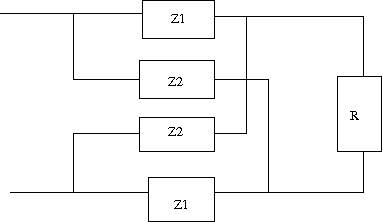さてこの回路の駆動点インピーダンスを求めるにはどうすんだっけ。ブリッジ回路なので簡単に式を立てることはできない。せっかくなので著者の解答とは異なる別解で解いてみよう。まず最初にZ1,Z2,RのΔ結線を等価なY結線に置き換えることによってZb+Z2直列回路とZc+Z1直列回路の並列接続にZaが直列接続された回路となり、駆動点インピーダンスが簡単に立てられるようになる。 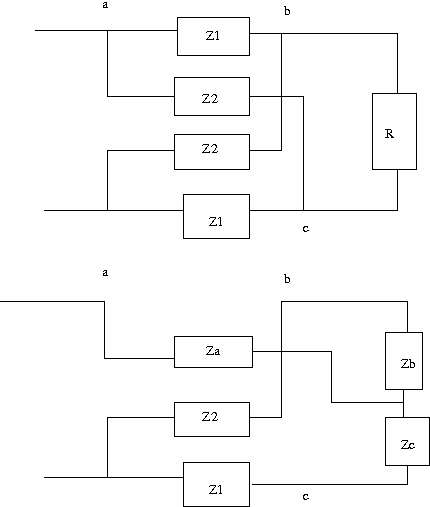$\begin{eqnarray}<br />Z(s)&=&Z_a+\frac{1}{\frac{1}{Z_b+Z_2}+\frac{1}{Z_c+Z_1}}\\<br />&=&Z_a+\frac{\left(Z_b+Z_2\right)\left(Z_c+Z_1\right)}{Z_1+Z_2+Z_b+Z_c}\\<br />&=&\frac{Z_1 Z_2}{Z_1+Z_2+R}+\frac{\left(\frac{Z_1 R}{Z_1+Z_2+R}+Z_2\right)\left(\frac{Z_2 R}{Z_1+Z_2+R}+Z_1\right)}{Z_1+Z_2+\frac{Z_1 R}{Z_1+Z_2+R}+\frac{Z_2 R}{Z_1+Z_2+R}}\\<br />&=&\frac{Z_1 Z_2}{Z_1+Z_2+R}+\frac{\left(\frac{\cancel{\left(Z_1+Z_2\right)}\left(R+Z_2\right)}{\cancel{Z_1+Z_2+R}}\right)\left(\frac{\left(Z_1+Z_2\right)\left(R+Z_1\right)}{Z_1+Z_2+R}\right)}{\frac{\cancel{\left(Z_1+Z_2\right)}\left(Z_1+Z_2+2R\right)}{\cancel{Z_1+Z_2+R}}}\\<br />&=&\frac{Z_1 Z_2}{Z_1+Z_2+R}+\frac{\left(Z_1+Z_2\right)\left(R+Z_2\right)\left(R+Z_1\right)}{\left(Z_1+Z_2+2R\right)\left(Z_1+Z_2+R\right)}\\<br />&=&\frac{Z_1 Z_2\left(Z_1+Z_2+2R\right)+\left(Z_1+Z_2\right)\left(R+Z_2\right)\left(R+Z_1\right)}{\left(Z_1+Z_2+2R\right)\left(Z_1+Z_2+R\right)}\\<br />&=&\frac{2 Z_1 Z_2\left(Z_1+Z_2\right)+R\left({Z_1}^2+2Z_1 Z_2+{Z_2}^2\right)+2R Z_1 Z_2+R^2\left(Z_1+Z_2\right)}{\left(Z_1+Z_2+2R\right)\left(Z_1+Z_2+R\right)}\\<br />&=&\frac{2 Z_1 Z_2\left(Z_1+Z_2\right)+R\left({Z_1}+{Z_2}\right)^2+R\left(2 Z_1 Z_2+R\left(Z_1+Z_2\right)\right)}{\left(Z_1+Z_2+2R\right)\left(Z_1+Z_2+R\right)}\\<br />&=&\frac{\left(Z_1+Z_2\right)\left(2 Z_1 Z_2+R\left({Z_1}+{Z_2}\right)\right)+R\left(2 Z_1 Z_2+R\left(Z_1+Z_2\right)\right)}{\left(Z_1+Z_2+2R\right)\left(Z_1+Z_2+R\right)}\\<br />&=&\frac{\cancel{\left(Z_1+Z_2+R\right)}\left(2 Z_1 Z_2+R\left(Z_1+Z_2\right)\right)}{\left(Z_1+Z_2+2R\right)\cancel{\left(Z_1+Z_2+R\right)}}\\<br />&=&\frac{2Z_1 Z_2+R\left(Z_1+Z_2\right)}{Z_1+Z_2+2R}\\<br />&=&\frac{2R^2+R\left(Z_1+Z_2\right)}{Z_1+Z_2+2R}\\<br />&=&\frac{R\cancel{\left(Z1+Z2+2R\right)}}{\cancel{Z_1+Z_2+2R}}\\<br />&=&R<br />Z_a&=&\frac{Z_1 Z_2}{Z_1+Z_2+R}\\<br />Z_b&=&\frac{Z_1 R}{Z_1+Z_2+R}\\<br />Z_c&=&\frac{Z_2 R}{Z_1+Z_2+R}\\<br />\end{eqnarray}$ ということで定抵抗回路となる。 Maxmaで処理すればfactor一発で答えが出るのだけれども、同じ結果を手計算で得ようとしたら予想外に式の操作が大変だった。更なる別解として等価電圧源と重ね合わせの理で導く方法も考えられるが、読者の課題としよう。

webadm	投稿日時: 2010-4-30 10:59
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3088	【30】まだまだ：逆回路逆回路の問題は続くよ。次はどちらかというと前問の応用問題。回路をよーく見比べてみよう。２つの回路をいずれもR1の定抵抗回路にしたいが、Z1とZ0をどのような回路にすればよいかという問題。 (a)は前問の最初の回路から、(b)は前問の最後の回路からヒントを得られる。 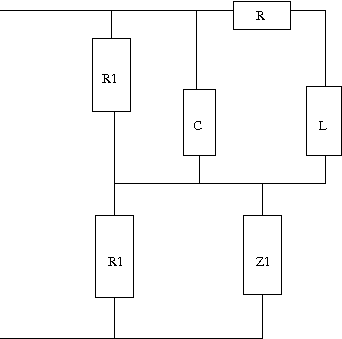(a)のRLC回路部分のインピーダンスをZ2とすると、前問よりZ1とZ2をR1に対する逆回路にすればよいわけで RLC回路部分のインピーダンスZ2はCとRL直列回路の並列接続であるので $\begin{eqnarray}<br />Z_2(s)&=&\frac{1}{C s+\frac{1}{R+L s}}<br />\end{eqnarray}$ 従ってZ1は $\begin{eqnarray}<br />Y_1(s)&=&\frac{1}{{R_1}^2}\frac{1}{C s+\frac{1}{R+L s}}\\<br />&=&\frac{1}{L_1 s+\frac{1}{G+C_1 s}}\\<br />L_1&=&C{R_1}^2\\<br />G_1&=&\frac{R}{{R_1}^2}\\<br />C_1&=&\frac{L}{{R_1}^2}<br />\end{eqnarray}$ となり、LとRC並列回路の直列接続となる。回路図に描くと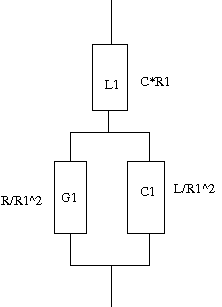ということになる。 (b)の回路についても同様に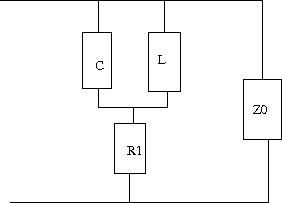前問の最後の設問にある回路と同様にZ0はR1と直列に左のLC並列回路とR1に対する逆回路であれば回路全体がR1の定抵抗回路になることから $begin{eqnarray}<br />Z_0(s)&=&R_1+{R_1}^2\left(C s+\frac{1}{L s}\right)\\<br />&=&R_1+L_0 s +\frac{1}{C_0 s}\\<br />L_0&=&C{R_1}^2\\<br />C_0&=&\frac{L}{{R_1}^2}<br />\end{eqnarray}$ 従ってR1とLとCの直列回路ということになる。回路図に描くと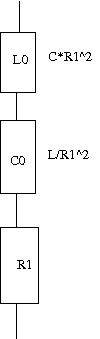ということになる。

webadm	投稿日時: 2010-4-30 10:15
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3088	【29】続々：逆回路次は逆回路の最後の問題。 Z1,Z2が互いにRに対する逆回路である場合に、以下の回路が定抵抗回路となることを示せというもの。駆動点インピーダンスはR^2=Z1Z2なる関係が成り立つ場合 $\begin{eqnarray}<br />Z(s)&=&\frac{1}{\frac{1}{R}+\frac{1}{Z_1}}+\frac{1}{\frac{1}{R}+\frac{1}{Z_2}}\\<br />&=&\frac{R Z_1}{R+Z_1}+\frac{R Z_2}{R+Z_2}\\<br />&=&\frac{R Z_1\left(R+Z_2\right)+R Z_2\left(R+Z_1\right)}{\left(R+Z_1\right)\left(R+Z_2\right)}\\<br />&=&\frac{R\left(R \left(Z_1+Z_2\right)+2 Z_1 Z_2\right)}{R^2+\left(Z_1+Z_2\right)R+Z_1 Z_2}\\<br />&=&\frac{R^2\left(\left(Z_1+Z_2\right)+2 R\right)}{R\left(2R+\left(Z_1+Z_2\right)\right)}\\<br />&=&R<br />\end{eqnarray}$ となり定抵抗回路となる。もう一方の回路についても同様に 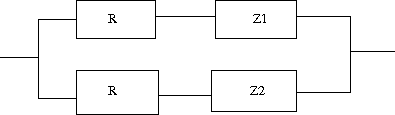R^2=Z1Z2が成り立つとすると駆動点インピーダンスは $\begin{eqnarray}<br />Z(s)&=&\frac{1}{\frac{1}{R+Z_1}+\frac{1}{R+Z_2}}\\<br />&=&\frac{\left(R+Z_1\right)\left(R+Z_2\right)}{2R+Z_1+Z_2}\\<br />&=&\frac{R^2+\left(Z_1+Z_2\right)R+Z_1 Z_2}{2R+Z_1+Z_2}\\<br />&=&\frac{R\left(2R+Z_1+Z_2\right)}{2R+Z_1+Z_2}\\<br />&=&R<br />\end{eqnarray}$ となり定抵抗回路となる。

webadm	投稿日時: 2010-4-30 9:49
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3088	【28】続：逆回路次も逆回路。今度は与えられた回路のR=100に対する逆回路を求める問題。 Rに対する逆回路とはZ1とZ2が互いに逆回路の場合に $Z_1 Z_2=R^2$ が成り立つものを言う。Rは定数である。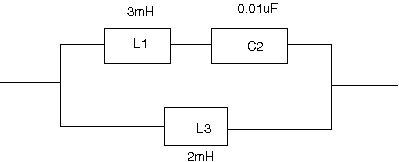駆動点インピーダンス関数を回路から起こすと $\begin{eqnarray}<br />Z_1(s)&=&\frac{1}{\frac{1}{L_1 s+\frac{1}{C_2 s}}+\frac{1}{L_3 s}}<br />\end{eqnarray}$ 従って逆回路は $\begin{eqnarray}<br />Y_2&=&\frac{1}{R^2}Z_1(s)\\<br />&=&\frac{1}{R^2}\frac{1}{\frac{1}{L_1 s+\frac{1}{C_2 s}}+\frac{1}{L_3 s}}\\<br />&=&\frac{1}{\frac{1}{C_1 s+\frac{1}{L_2 s}}+\frac{1}{C_3 s}}\\<br />C_1&=&\frac{L_1}{R^2}=\frac{3\times10^{-3}}{100^2}\\<br />&=&0.3\,[\mu F]\\<br />L_2&=&C_2 R^2=0.01\times10^{-6}\times100^2\\<br />&=&0.1\,[mH]\\<br />C_3&=&\frac{L_3}{R^2}=\frac{2\times10^{-3}}{100^2}\\<br />&=&0.2\,[\mu F]\\<br />\end{eqnarray}$ ということでLC並列回路とCの直列接続となる。回路図で表すと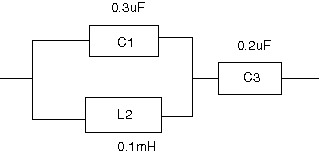ということになる。

webadm	投稿日時: 2010-4-29 19:35
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3088	【27】逆回路ふう残すところあと7問。ここからしばらく逆回路の問題。以下の回路の逆回路を求めよというもの。この回路は駆動点インピーダンス関数で表すと $Z_1(s)=L_0 s$ s=0に零点、s=∞に極を持ちスケーリングファクタはL0ということになる。したがって逆回路の駆動点インピーダンス関数はs=0に極、s=∞に零点を持ちスケーリングファクタが1/L0に比例する。 $begin{eqnarray}<br />{Y_1}^\'(s)&=&Z_1(s)<br />&=&L_0 s\\<br />&=&C_0 s\\<br />C_0&=&L_0<br />\end{eqnarray}$ ということになる。回路図上ではLの双対であるCに置き換わることになる。従って逆回路の回路はとなる。次はLC直列回路駆動点インピーダンス関数は $\begin{eqnarray}<br />{Z_2}(s)&=&L_1 s+\frac{1}{C_2 s}<br />\end{eqnarray}$ 従って逆回路は $\begin{eqnarray}<br />{Y_2}^\'(s)&=&Z_2(s)\\<br />&=&L_1 s+\frac{1}{C_2 s}\\<br />&=&C_1 s+\frac{1}{L_2 s}<br />C_1&=&L_1\\<br />L_2&=&C_2<br />\end{eqnarray}$ 回路図的にはLがCへCがLへ、直列接続が並列接続に変わる。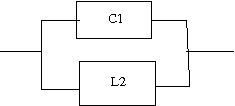次はLとLC並列回路の直列接続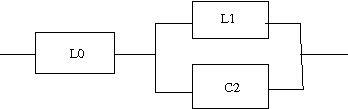駆動点インピーダンス関数は $\begin{eqnarray}<br />Z_3(s)&=&L_0 s+\frac{1}{L_1 s+\frac{1}{C_2 s}}<br />\end{eqnarray}$ 従って逆回路は $\begin{eqnarray}<br />{Y_3}^\'(s)&=&Z_3(s)\\<br />&=&L_0 s+\frac{1}{L_1 s+\frac{1}{C_2 s}}\\<br />&=&C_0 s+\frac{1}{C_1 s+\frac{1}{L_2 s}}\\<br />C_0&=&L_0\\<br />C_1&=&L_1\\<br />L_2&=&C_2<br />\end{eqnarray}$ 従ってCとLC直列回路の並列接続となる。回路図に描くと 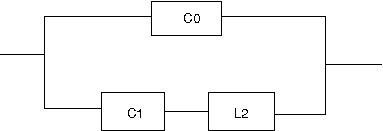s=0,∞以外にも複数の特異点を持つ場合、同じ回路が複数形存在することはFoster展開やCauer展開で学んだとおり。元の回路のインピーダンスは逆回路のアドミッタンスとなる点を利用すれば最も簡単に双対となる回路を導くことができる。次は２つのLC並列回路の直列接続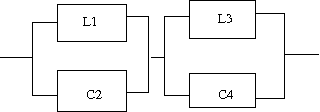関数で表すと $\begin{eqnarray}<br />Z_4(s)&=&\frac{1}{\frac{1}{L_1 s}+C_2 s}+\frac{1}{\frac{1}{L_3 s}+C_4 s}<br />\end{eqnarray}$ 従って逆回路の関数は $\begin{eqnarray}<br />{Y_4}^\'&=&Z_4(s)\\<br />&=&\frac{1}{\frac{1}{L_1 s}+C_2 s}+\frac{1}{\frac{1}{L_3 s}+C_4 s}\\<br />&=&\frac{1}{\frac{1}{C_1 s}+L_2 s}+\frac{1}{\frac{1}{C_3 s}+L_4 s}\\<br />C_1&=&L_1\\<br />L_2&=&C_2\\<br />C_3&=&L_3\\<br />L_4&=&C_4<br />\end{eqnarray}$ ２つのLC直列回路の並列接続となる。回路図で表すと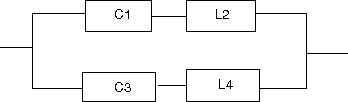最後はLとLC並列回路とCの直列接続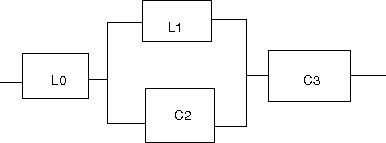駆動点インピーダンス関数は $\begin{eqnarray}<br />Z_5(s)&=&L_0 s+\frac{1}{\frac{1}{L_1 s}+C_2 s}+\frac{1}{C_3 s}<br />\end{eqnarray}$ 従って逆回路は $\begin{eqnarray}<br />{Y_5}^\'&=&Z_5(s)\\<br />&=&L_0 s+\frac{1}{\frac{1}{L_1 s}+C_2 s}+\frac{1}{C_3 s}\\<br />&=&C_0 s+\frac{1}{\frac{1}{C_1 s}+L_2 s}+\frac{1}{L_3 s}\\<br />C_0&=&L_0\\<br />C_1&=&L_1\\<br />L_2&=&C_2\\<br />L_3&=&C_3<br />\end{eqnarray}$ 従ってCとLC直列回路とLの並列接続となる。回路図に描くと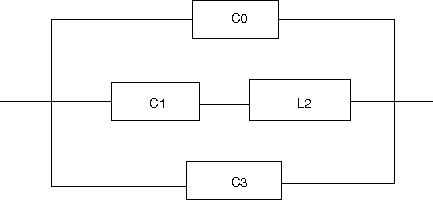ということになる。

webadm	投稿日時: 2010-4-28 9:20
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3088	【26】密結合変成器の分離次ぎは相互インダクタンスを伴うリアクタンス回路に関する問題。以下の回路の相互インダクタンスの結合係数kが1である場合、この回路に等価な相互インダクタンスを含まないLC回路を求めよというもの。この種の操作は密結合変成器の分離と呼ばれ変成器を伴わない二端子回路の構成法。結合係数は $k=M/sqrt{L_1 L_2}$ で定義されていたことを思い出そう。問題の回路は以下の様な等価回路に置き換えることができる。これより駆動点インピーダンスの式を起こすと $\begin{eqnarray}<br />Z(s)&=&\frac{1}{C_1 s}+\left(L_1-M\right)s+\frac{1}{\Large\frac{1}{M s+\frac{1}{C_2 s}}+\frac{1}{\left(L_2-M\right)s+\frac{1}{C_3 s}}}\\<br />&=&\frac{C_1\left(L_1-M\right)s^2+1}{C_1 s}+\frac{1}{\Large\frac{\frac{1}{M} s}{s^2+\frac{1}{C_2 M}}+\frac{\frac{1}{L_2-M}s}{s^2+\frac{1}{C_3\left(L_2-M\right)}}}\\<br />&=&\frac{\left(L_1-M\right)\left(s^2+\frac{1}{C_1\left(L_1-M\right)}\right)}{s}+\frac{\left(s^2+\frac{1}{C_2 M}\right)\left(s^2+\frac{1}{C_3\left(L_2-M\right)}\right)}{\left(s^2+\frac{1}{C_3\left(L_2-M\right)}\right)\frac{1}{M} s+\left(s^2+\frac{1}{C_2 M}\right)\frac{1}{L_2-M}s}\\<br />&=&\frac{\left(L_1-M\right)\left(s^2+\frac{1}{C_1\left(L_1-M\right)}\right)}{s}+\frac{\left(s^2+\frac{1}{C_2 M}\right)\left(s^2+\frac{1}{C_3\left(L_2-M\right)}\right)}{s\left(\frac{L_2}{M\left(L_2-M\right)}s^2+\frac{C_2+C_3}{C_2 C_3 M\left(L_2-M\right)}\right)}\\<br />&=&\frac{\left(L_1-M\right)\left(s^2+\frac{1}{C_1\left(L_1-M\right)}\right)}{s}+\frac{\frac{M\left(L_2-M\right)}{L_2}\left(s^2+\frac{1}{C_2 M}\right)\left(s^2+\frac{1}{C_3\left(L_2-M\right)}\right)}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\left(L_1-M\right)\left(s^2+\frac{1}{C_1\left(L_1-M\right)}\right)\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)+\frac{M\left(L_2-M\right)}{L_2}\left(s^2+\frac{1}{C_2 M}\right)\left(s^2+\frac{1}{C_3\left(L_2-M\right)}\right)}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\left(L_1-M\right)\left(s^4+\frac{L_2 C_2 C_3+C_1\left(L_1-M\right)\left(C_2+C_3\right)}{C_1\left(L_1-M\right)L_2 C_2 C_3}s^2+\frac{C_2+C_3}{C_1\left(L_1-M\right)L_2 C_2 C_3}\right)+\frac{M\left(L_2-M\right)}{L_2}\left(s^4+\frac{C_3\left(L_2-M\right)+C_2 M}{C_2 C_3 M\left(L_2-M\right)}s^2+\frac{1}{C_2 C_3 M\left(L_2-M\right)}\right)}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\left(\left(L_1-M\right)s^4+\frac{L_2 C_2 C_3+C_1\left(L_1-M\right)\left(C_2+C_3\right)}{C_1 L_2 C_2 C_3}s^2+\frac{C_2+C_3}{C_1 L_2 C_2 C_3}\right)+\left(\frac{M\left(L_2-M\right)}{L_2}s^4+\frac{C_3\left(L_2-M\right)+C_2 M}{L_2 C_2 C_3}s^2+\frac{1}{L_2 C_2 C_3}\right)}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\frac{L_1 L_2 -M^2}{L_2}s^4+\frac{L_2 C_2 C_3+C_1\left(L_1-M\right)\left(C_2+C_3\right)+C_1\left(C_3\left(L_2-M\right)+C_2 M\right)}{C_1 L_2 C_2 C_3}s^2+\frac{C_1+C_2+C_3}{C_1 L_2 C_2 C_3}}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\frac{L_1 L_2 -M^2}{L_2}s^4+\frac{L_2 C_2 C_3+L_1 C_1 C_2+L_1 C_1 C_3+L_2 C_1 C_3 -2 M C_1 C_3}{C_1 L_2 C_2 C_3}s^2+\frac{C_1+C_2+C_3}{C_1 L_2 C_2 C_3}}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />\end{eqnarray}$ ここで題意よりk=1であることから $L_1 L_2-M^2=0$ ということになり、式は以下の様になり題意より定数を代入すると。 $\begin{eqnarray}<br />Z(s)&=&\frac{\frac{L_2 C_2 C_3+L_1 C_1 C_2+L_1 C_1 C_3+L_2 C_1 C_3 -2 M C_1 C_3}{C_1 L_2 C_2 C_3}s^2+\frac{C_1+C_2+C_3}{C_1 L_2 C_2 C_3}}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\frac{8\times 1\times 1+2\times 2\times 1+2\times 2\times 1+8\times 2\times 1 -2 \sqrt{2\times 8}\times 2\times 1}{2\times 8\times 1\times 1}s^2+\frac{2+1+1}{2\times 8\times 1\times 1}}{s\left(s^2+\frac{1+1}{8\times 1\times 1}\right)}\\<br />&=&\frac{s^2+\frac{1}{4}}{s\left(s^2+\frac{1}{4}\right)}\\<br />&=&\frac{1}{s}\\<br />&=&\frac{1}{C s}\\<br />C&=&1\,[F]<br />\end{eqnarray}$ ということでただ一個のキャパシタンスと等価になる。一方で相互インダクタンスのもうひとつの等価回路について調べるとこれより駆動点インピーダンスの式を起こすと $\begin{eqnarray}<br />Z(s)&=&\frac{1}{C_1 s}+\left(L_1+M\right)s+\frac{1}{\Large\frac{1}{-M s+\frac{1}{C_2 s}}+\frac{1}{\left(L_2+M\right)s+\frac{1}{C_3 s}}}\\<br />&=&\frac{C_1\left(L_1+M\right)s^2+1}{C_1 s}+\frac{1}{\Large-\frac{\frac{1}{M} s}{s^2-\frac{1}{C_2 M}}+\frac{\frac{1}{L_2+M}s}{s^2+\frac{1}{C_3\left(L_2+M\right)}}}\\<br />&=&\frac{\left(L_1+M\right)\left(s^2+\frac{1}{C_1\left(L_1+M\right)}\right)}{s}+\frac{\left(s^2-\frac{1}{C_2 M}\right)\left(s^2+\frac{1}{C_3\left(L_2+M\right)}\right)}{-\left(s^2+\frac{1}{C_3\left(L_2+M\right)}\right)\frac{1}{M} s+\left(s^2-\frac{1}{C_2 M}\right)\frac{1}{L_2+M}s}\\<br />&=&\frac{\left(L_1+M\right)\left(s^2+\frac{1}{C_1\left(L_1+M\right)}\right)}{s}-\frac{\left(s^2-\frac{1}{C_2 M}\right)\left(s^2+\frac{1}{C_3\left(L_2+M\right)}\right)}{s\left(\frac{L_2}{M\left(L_2+M\right)}s^2+\frac{C_2+C_3}{C_2 C_3 M\left(L_2-M\right)}\right)}\\<br />&=&\frac{\left(L_1+M\right)\left(s^2+\frac{1}{C_1\left(L_1+M\right)}\right)}{s}-\frac{\frac{M\left(L_2+M\right)}{L_2}\left(s^2-\frac{1}{C_2 M}\right)\left(s^2+\frac{1}{C_3\left(L_2+M\right)}\right)}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\left(L_1+M\right)\left(s^2+\frac{1}{C_1\left(L_1+M\right)}\right)\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)-\frac{M\left(L_2+M\right)}{L_2}\left(s^2-\frac{1}{C_2 M}\right)\left(s^2+\frac{1}{C_3\left(L_2+M\right)}\right)}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\left(L_1+M\right)\left(s^4+\frac{L_2 C_2 C_3+C_1\left(L_1+M\right)\left(C_2+C_3\right)}{C_1\left(L_1+M\right)L_2 C_2 C_3}s^2+\frac{C_2+C_3}{C_1\left(L_1+M\right)L_2 C_2 C_3}\right)-\frac{M\left(L_2+M\right)}{L_2}\left(s^4-\frac{C_3\left(L_2-M\right)-C_2 M}{C_2 C_3 M\left(L_2+M\right)}s^2-\frac{1}{C_2 C_3 M\left(L_2+M\right)}\right)}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\left(\left(L_1+M\right)s^4+\frac{L_2 C_2 C_3+C_1\left(L_1+M\right)\left(C_2+C_3\right)}{C_1 L_2 C_2 C_3}s^2+\frac{C_2+C_3}{C_1 L_2 C_2 C_3}\right)-\left(\frac{M\left(L_2+M\right)}{L_2}s^4-\frac{C_3\left(L_2+M\right)-C_2 M}{L_2 C_2 C_3}s^2-\frac{1}{L_2 C_2 C_3}\right)}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\frac{L_1 L_2 -M^2}{L_2}s^4+\frac{L_2 C_2 C_3+C_1\left(L_1+M\right)\left(C_2+C_3\right)+C_1\left(C_3\left(L_2+M\right)-C_2 M\right)}{C_1 L_2 C_2 C_3}s^2+\frac{C_1+C_2+C_3}{C_1 L_2 C_2 C_3}}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\frac{L_1 L_2 -M^2}{L_2}s^4+\frac{L_2 C_2 C_3+L_1 C_1 C_2+L_1 C_1 C_3+L_2 C_1 C_3 +2 M C_1 C_3}{C_1 L_2 C_2 C_3}s^2+\frac{C_1+C_2+C_3}{C_1 L_2 C_2 C_3}}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />\end{eqnarray}$ 一カ所だけ符号が異なるだけである。同様にk=1の時は分子の４次の項は消滅するので、定数を代入すると $\begin{eqnarray}<br />Z(s)&=&\frac{\frac{L_2 C_2 C_3+L_1 C_1 C_2+L_1 C_1 C_3+L_2 C_1 C_3 +2 M C_1 C_3}{C_1 L_2 C_2 C_3}s^2+\frac{C_1+C_2+C_3}{C_1 L_2 C_2 C_3}}{s\left(s^2+\frac{C_2+C_3}{L_2 C_2 C_3}\right)}\\<br />&=&\frac{\frac{8\times 1\times 1+2\times 2\times 1+2\times 2\times 1+8\times 2\times 1 +2 \sqrt{2\times 8}\times 2\times 1}{2\times 8\times 1\times 1}s^2+\frac{2+1+1}{2\times 8\times 1\times 1}}{s\left(s^2+\frac{1+1}{8\times 1\times 1}\right)}\\<br />&=&\frac{3s^2+\frac{1}{4}}{s\left(s^2+\frac{1}{4}\right)}\\<br />&=&\frac{3\left(s^2+\frac{1}{12}\right)}{s\left(s^2+\frac{1}{4}\right)}\\<br />&=&\frac{H_0}{s}+\frac{H_1 s}{s^2+\frac{1}{4}}\\<br />&=&\frac{1}{C s}+\frac{1}{{C_1}^\'s+\frac{1}{L_1 s}}\\<br />C&=&\frac{1}{H_0}=1\,[F]<br />{C_1}^\'&=&\frac{1}{H_1}=\frac{1}{2}\,[F]\\<br />L_1&=&4 H_1=8\,[H]\\<br />H_0&=&\lim_{s\to0}s Z(s)\\<br />&=&\left.\frac{3\left(s^2+\frac{1}{12}\right)}{\left(s^2+\frac{1}{4}\right)}\right\|_{s=0}\\<br />&=&\frac{3\left(\frac{1}{12}\right)}{\left(\frac{1}{4}\right)}\\<br />&=&1<br />H_1&=&\lim_{s\to-\frac{1}{4}}\frac{\left(s^2+\frac{1}{4}\right)Z(s)}{s}\\<br />&=&\left.\frac{3\left(s^2+\frac{1}{12}\right)}{s^2}\right\|_{s=\frac{1}{4}}\\<br />&=&\frac{3\left(-\frac{1}{4}+\frac{1}{12}\right)}{-\frac{1}{4}}\\<br />&=&2<br />\end{eqnarray}$ ということになる。回路図に描くとといことになる。

webadm	投稿日時: 2010-4-27 10:19
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3088	【25】続：アドミッタンス関数勝手に題名を付けているが、たぶんアドミッタンス関数で考えた方が易しいのではと。ある回路と並列に抵抗R=3[Ω]を接続したときのインピーダンス関数が以下の通り既知である場合、元の回路のインピーダンス関数を求めよというもの。 $\frac{9s^2+15}{s^3+3s^2+4s+5}$ 並列接続回路なのでアドミッタンス関数として考えよう。元の回路のアドミッタンス関数をY0とすると、抵抗を並列に接続した後のアドミッタンス関数をYとする。その場合、以下の関係が成り立つ。 $\begin{eqnarray}<br />Y(s)&=&Y_0(s)+\frac{1}{R}\\<br />&=&Y_0(s)+\frac{1}{3}\\<br />&=&\frac{s^3+3s^2+4s+5}{9s^2+15}<br />\end{eqnarray}$ 従って元のインピーダンス関数をZ0とすると $\begin{eqnarray}<br />Z_0(s)&=&\frac{1}{Y_0(s)}\\<br />&=&\frac{1}{\Large\frac{s^3+3s^2+4s+5}{9s^2+15}-\frac{1}{3}}\\<br />&=&\frac{1}{\Large\frac{3\left(s^3+3s^2+4s+5\right)-\left(9s^2+15\right)}{3\left(9s^2+15\right)}}\\<br />&=&\frac{\left(9s^2+15\right)}{\left(s^3+\cancel{3s^2}+4s+\cancel{5}\right)-\left(\cancel{3s^2}+\cancel{5}\right)}\\<br />&=&\frac{9s^2+15}{s\left(s^2+4\right)}\\<br />&=&\frac{H_0}{s}+\frac{H_1 s}{s^2+4}\\<br />&=&\frac{1}{C_0 s}+\frac{1}{C_1 s+\frac{1}{L_1 s}}\\<br />C_0&=&\frac{1}{H_0}=\frac{4}{15}\,[F]\\<br />C_1&=&\frac{1}{H_1}=\frac{4}{21}\,[F]\\<br />L_1&=&\frac{H_1}{4}=\frac{21}{16}\,[H]\\<br />H_0&=&\lim_{s\to0}s Z_0(s)\\<br />&=&\left.\frac{9s^2+15}{\left(s^2+4\right)}\right\|_{s=0}\\<br />&=&\frac{15}{4}\\<br />H_1&=&\lim_{s^2=-4}\frac{\left(s^2+4\right)Z_0(s)}{s}\\<br />&=&\left.\frac{9s^2+15}{s^2}\right\|_{s^2=-4}\\<br />&=&\frac{9\left(-4\right)+15}{-4}\\<br />&=&\frac{21}{4}<br />\end{eqnarray}$ ということになる。回路図に描くとということになる。

webadm	投稿日時: 2010-4-24 20:47
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3088	【24】アドミッタンス関数今度は趣向が変わった問題。以下の様なRLC回路と等価なRC回路を実現するためのCの値の条件と等価回路を示せというもの。この回路はLとCを含むためωによって誘導性と容量性のどちらかのリアクタンスを持つ。題意の等価なRC回路というのはω≠0で容量性リアクタンスのみを持つようにするという意味になる。従って与えられた元のRLC回路がすべてのωに関して容量性リアクタンスのみ持つようになるCの条件を求めれば良いことになる。問題の回路のサセプタンスが常に容量性になるには $\begin{eqnarray}<br />B(\omega)&=&Im\left(Y(j\omega)\right)\\<br />&=&Im\left(\frac{1}{R_0}+j C_\infty \omega+\frac{1}{j L_1 \omega+R_1}+\frac{1}{R_2-j\frac{1}{C \omega}}\right)\\<br />&=&Im\left(\frac{1}{R_0}+j C_\infty \omega+\frac{R_1-j L_1 \omega}{{L_1}^2 {\omega}^2+{R_1}^2}+\frac{R_2+j\frac{1}{C \omega}}{{R_2}^2+\frac{1}{C^2 {\omega}^2}}\right)\\<br />&=&C_\infty \omega-\frac{L_1 \omega}{{L_1}^2 {\omega}^2+{R_1}^2}+\frac{\frac{1}{C \omega}}{{R_2}^2+\frac{1}{C^2 {\omega}^2}}\\<br />&=&\omega\left(C_\infty-\frac{L_1}{{L_1}^2 {\omega}^2+{R_1}^2}+\frac{C}{C^2 {R_2}^2{\omega}^2+1}\right)\\<br />&=&\omega\left(C_\infty+\frac{\left({L_1}^2 {\omega}^2+{R_1}^2\right)C-\left(C^2 {R_2}^2{\omega}^2+1\right)L_1 }{\left({L_1}^2 {\omega}^2+{R_1}^2\right)\left(C^2 {R_2}^2{\omega}^2+1\right)}\right)\\<br />&=&\omega\left(C_\infty+\frac{C L_1\left({L_1} - C {R_2}^2\right){\omega}^2+\left(C{R_1}^2-L_1\right)}{\left({L_1}^2 {\omega}^2+{R_1}^2\right)\left(C^2 {R_2}^2{\omega}^2+1\right)}\right)\ge0\,\forall\omega<br />\end{eqnarray}$ を満たす必要がある。すなわちCの値が $\begin{eqnarray}<br />{L_1} - C {R_2}^2&\ge&0<br />C{R_1}^2-L_1&\ge&0<br />\end{eqnarray}$ を同時に満たす必要がある。整理して与えられた定数を代入すると $\begin{eqnarray}<br />\frac{L_1}{{R_2}^2}\ge &C& \ge \frac{L_1}{{R_1}^2}\\<br />24 \ge &C& \ge \frac{2}{3}<br />\end{eqnarray}$ こっからどうすんだ。見通しが悪かった。どうやら著者の判りにくい解答を理解すると題意を読み違えていたようだ。角周波数領域だけで物事を考えていたのが間違いで、複素角周波数領域で考えないといけなかった。従って回路からアドミッタンス関数を起こすと $\begin{eqnarray}<br />Y(s)&=&\frac{1}{R_0}+C_\infty s+\frac{1}{L_1 s+R_1}+\frac{1}{R_2+\frac{1}{C s}}\\<br />&=&\frac{1}{R_0}+C_\infty s+\frac{\frac{1}{L_1}}{s+\frac{R_1}{L_1}}+\frac{\frac{ s}{R_2}}{s+\frac{1}{C R_2}}<br />\end{eqnarray}$ この関数はs=-R1/L1,-1/C*R2,∞の３つの極を持つことになる。従ってRL直列回路とRC直列回路にそれぞれが独立した極を持つので三種類の素子が必要になってしまう。問題の趣旨は、RL直列回路とRC直列回路が同一の極（重根）をもつようにし、なおかつ全体的に容量性（留数が負）になるようにせよということだった。重根を持たせるにはCの値を $\begin{eqnarray}<br />\frac{R_1}{L_1}&=& \frac{1}{C R_2}\\<br />C&=&\frac{L_1}{R_1 R_2}\\<br />&=&\frac{6}{3\times \frac{1}{2}}=4\,[F]<br />\end{eqnarray}$ とすればよい。さてあとはRC回路のみでどう実現されるかだが、見通しができていない(´д` ) 実は良く判ってなかったのである。ちなみにC=8として問題の回路のサセプタンス値を3Dでプロットしてみるとs=-0.25とs=-0.5に極が現れているのが確認できる。前者は容量性サセプタンス項、後者は誘導性サセプタンス項のもの。両者は互いに山と谷の極性が逆方向なのと留数の絶対値が容量性の方が勝っているので容量性側の起伏が大きい、Cの値を変更して容量性の極を誘導性の極の上に重ねると誘導性は消滅し、容量性のみが残ると予想される。C=4にすると双方の極がs=-0.5で重なる。見事に誘導性の痕跡は消え失せて容量性の極だけが残っている。著者の解答にある負の留数ってなんだという疑問が沸く。回路から起こしたアドミッタンス関数の式には負の留数などないように見える。しかしRC直列回路のアドミッタンス項は分子と分母の次数が同じなので以下の様に更に部分分数展開できることに気づくべきだった。 $\begin{eqnarray}<br />Y(s)&=&\frac{1}{R_0}+C_\infty s+\frac{\frac{1}{L_1}}{s+\frac{R_1}{L_1}}+\frac{\frac{ s}{R_2}}{s+\frac{1}{C R_2}}\\<br />&=&\frac{1}{R_0}+C_\infty s+\frac{\frac{1}{L_1}}{s+\frac{R_1}{L_1}}+\frac{1}{R_2}-\frac{\frac{1}{C {R_2}^2}}{s+\frac{1}{C R_2}}<br />\end{eqnarray}$ 確かに負の留数が現れる。そこで先ほど導いたCの値を代入して容量性になるように数式を操作してみると $\begin{eqnarray}<br />Y(s)&=&\frac{1}{R_0}+C_\infty s+\frac{\frac{1}{L_1}}{s+\frac{R_1}{L_1}}+\frac{1}{R_2}-\frac{\frac{1}{C {R_2}^2}}{s+\frac{1}{C R_2}}\\<br />&=&\frac{1}{R_0}+C_\infty s+\frac{1}{R_2}-\frac{\frac{R_1}{L_1 {R_2}}-\frac{1}{L_1 }}{s+\frac{R_1}{L_1 }}\\<br />&=&\frac{1}{R_0}+C_\infty s+\frac{1}{R_2}-\frac{\frac{1}{L_1}\left(\frac{R_1}{{R_2}}-1\right)}{s+\frac{R_1}{L_1 }}\\<br />&=&\frac{1}{R_0}+C_\infty s+\frac{1}{R_2}-\frac{\frac{R_1}{L_1}\left(\frac{1}{{R_2}}-\frac{1}{R_1}\right)}{s+\frac{R_1}{L_1 }}\\<br />&=&\frac{1}{R_0}+C_\infty s+\frac{1}{R_2}-\left(\frac{1}{R_2}-\frac{1}{R_1}\right)+\left(\left(\frac{1}{R_2}-\frac{1}{R_1}\right)-\frac{\frac{R_1}{L_1}\left(\frac{1}{{R_2}}-\frac{1}{R_1}\right)}{s+\frac{R_1}{L_1 }}\right)\\<br />&=&\frac{1}{R_0}+C_\infty s+\frac{1}{R_1}+\frac{\left(\frac{1}{R_2}-\frac{1}{R_1}\right)s}{s+\frac{R_1}{L_1 }}\\<br />&=&\frac{1}{R_0}+C_\infty s+\frac{1}{R_1}+\frac{\frac{R_1-R_2}{R_1 R_2}s}{s+\frac{R_1}{L_1 }}\\<br />&=&\frac{R_0+R_1}{R_0 R_1}+C_\infty s+\frac{1}{\frac{R_1 R_2}{R_1-R_2}+\frac{R_1^2 R_2}{L_1\left(R_1-R_2\right)s}}\\<br />&=&\frac{1}{{R_0}^\'}+C_\infty s+\frac{1}{{R_1}^\'+\frac{1}{{C_1}^\' s}}\\<br />R_0&=&4\,[\Omega]\\<br />C_\infty&=&3\,[F]\\<br />R_1&=&3\,[\Omega]\\<br />L_1&=&6\,[H]\\<br />R_2&=&\frac{1}{2}\,[\Omega]\\<br />{R_0}^\'&=&\frac{R_0 R_1}{R_0+R_1}=\frac{4\times 3}{4+3}=\frac{12}{7}\,[\Omega]\\<br />{R_1}^\'&=&\frac{R_1 R_2}{R_1-R_2}=\frac{3\times \frac{1}{2}}{3-\frac{1}{2}}=\frac{3}{5}\,[\Omega]\\<br />{C_1}^\'&=&\frac{L_1\left(R_1-R_2\right)}{R_1^2 R_2}=\frac{6\left(3-\frac{1}{2}\right)}{3^2\times \frac{1}{2}}=\frac{10}{3}\,[F]<br />\end{eqnarray}$ ということになる。回路図で表すとというわけでRC回路で実現できる。やっとわかったよﾏﾏﾝ(ﾉ∀`) 上記の方法以外にも、極がs=-R1/L1,∞のみとなるCの値を元のアドミッタンス関数に代入してs=0、s=-R1/L1に関する留数(H0,H1)を求めれば手品的な計算無しで同じ結果が得られると思われる。それは簡単なので読者の課題としよう(´∀` ) と思ったけどせっかくなので以下に別解を示すことにしよう。 $\begin{eqnarray}<br />Y(s)&=&\frac{1}{R_0}+C_\infty s+\frac{\frac{1}{L_1}}{s+\frac{R_1}{L_1}}+\frac{1}{R_2}-\frac{\frac{R_1}{L_1 {R_2}}}{s+\frac{R_1}{L_1}}\\<br />&=&H_0+H_\infty s+\frac{H_1 s}{s+\frac{R_1}{L_1}}\\<br />&=&\frac{1}{{R_0}^\'}+C_\infty s+\frac{1}{{R_1}^\'+\frac{1}{{C_1}^\' s}}\\<br />R_0&=&4\,[\Omega]\\<br />C_\infty&=&3\,[F]\\<br />R_1&=&3\,[\Omega]\\<br />L_1&=&6\,[H]\\<br />R_2&=&\frac{1}{2}\,[\Omega]\\<br />{R_0}^\'&=&\frac{1}{H_0}\\<br />&=&\frac{R_0 R_1}{R_0+R_1}=\frac{4\times 3}{4+3}\\<br />&=&\frac{12}{7}\,[\Omega]\\<br />{R_1}^\'&=&\frac{1}{H_1}=\frac{R_1 R_2}{R_1-R_2}\\<br />&=&\frac{3\times \frac{1}{2}}{3-\frac{1}{2}}\\<br />&=&\frac{3}{5}\,[\Omega]\\<br />{C_1}^\'&=&\frac{H_1}{\frac{R_1}{L_1}}\\<br />&=&\frac{\frac{R_1-R_2}{R_1 R_2}}{\frac{R_1}{L_1}}\\<br />&=&\frac{L_1\left(R_1-R_2\right)}{{R_1}^2 R_2}\\<br />&=&\frac{6\left(3-\frac{1}{2}\right)}{{3}^2\times \frac{1}{2}}\\<br />&=&\frac{10}{3}\,[F]\\<br />H_0&=&\lim_{s\to0}Y(s)\\<br />&=&\left.\frac{1}{R_0}+C_\infty s+\frac{\frac{1}{L_1}}{s+\frac{R_1}{L_1}}+\frac{1}{R_2}-\frac{\frac{R_1}{L_1 {R_2}}}{s+\frac{R_1}{L_1}}\right\|_{s=0}\\<br />&=&\frac{1}{R_0}+\frac{1}{R_1 }+\cancel{\frac{1}{R_2}}-\cancel{\frac{1}{R_2}}\\<br />&=&\frac{R_0+R_1}{R_0 R_1}\\<br />H_1&=&\lim_{s\to-\frac{R_1}{L_1}}\frac{\left(s+\frac{R_1}{L_1}\right)Y(s)}{s}\\<br />&=&\left.\frac{\frac{1}{L_1}}{s}-\frac{\frac{R_1}{L_1 {R_2}}}{s}\right\|_{s=-\frac{R_1}{L_1}}\\<br />&=&\frac{\frac{1}{L_1}}{-\frac{R_1}{L_1}}-\frac{\frac{R_1}{L_1 {R_2}}}{-\frac{R_1}{L_1}}\\<br />&=&\frac{1}{R_2}-\frac{1}{R_1}\\<br />&=&\frac{R_1-R_2}{R_1 R_2}<br />\end{eqnarray}$ なんだ簡単じゃないか(´∀` )

(1) 2 3 4 »

スレッド表示 | 古いものから

前のトピック | 次のトピック | トップ

投稿するにはまず登録を