| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2009-10-22 7:47 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3088 |
リアクタンス関数 戦前の1924年に米国ベル研究所の研究者Ronald Fosterの論文"A Reactance Theorem"が発表され、回路網合成の歴史が動き始めた。
Fosterは駆動点インピーダンス(driving point impedance)という言葉を用いインダクタンスとキャパシタンスのみから成り抵抗を含まない2端子回路が複素周波数変数を用いた代数式によって表され、その式を部分分数に展開すれば対応する回路が合成できることと、その必要十分条件を初めて示した。この時既にLCのみの回路に限定されるが正実関数の定義が与えられている。 当時米国に居たドイツ人CauerはFosterの論文に触発され、すぐさまその拡張と一般化のアイデアを得、Fosterの仕事の続きをすることになる。Cauerは抵抗を含む2端子回路にも適用できるようにFosterのリアクタンス理論を拡張し、更にラダー接続回路の合成が可能な連分数展開も組み入れた。これは後に次ぎに学ぶことになる。 最初のOtto Bruneの正実関数が出てきて歴史的に逆になってしまうが、ここでようやく最初に登場したFosterのリアクタンス理論から学ぶことにしよう。 最初に1端子対回路(2端子回路)はn端子対回路の一端子対以外を除いてすべて短絡した回路と考えると一般化することができる。 左のn端子対回路では以下の回路方程式が成り立つ 一方1端子対回路ではポート1以外をすべて短絡したのと等価なので端子電圧は0となり ということになる。従って両辺にインピーダンスマトリックスの逆行列を乗じると ただし I1について解くと 従ってポート1の駆動点インピーダンスは ということになる。 インピーダンスマトリックスの任意の要素Zijが損失の無いLとCからなるとするとs=jωとすると ここで と置くと 従って ここで 同様に 従って駆動点インピーダンスZ(s)は 従って分子が偶関数で分母が奇関数の有理関数となる。分子と分母の式を多項式に展開すると分子の式の次数は2nで分母の次数は一つ少ない2n-1となる。 は駆動点インピーダンスが0となる零点である。 また は駆動点インピーダンスが∞となる極である。 ただし であるケースでは、 となり、最後の式の分母のsと相殺されて分子が奇関数で分母が偶関数となり こんどはω=0が極ではなく零点となる。この場合でも分子と分母を展開して多項式にすると分子の次数は2n-1で分母の次数は2n-2である。依然として分母の次数が分子より1少ない。 また同じ値を零点と極で持つ場合には、分子と分母で相殺されてそれは零点でも極でも無くなる。 ところで の場合には、駆動点インピーダンスはどうなるのだろうか? いろいろ調べると全部でパターンが4つあるらしいが、2つほど納得がいかん(;´Д`) どうやら先に導いた2つの駆動点インピーダンスの式においてω=∞に零点もしくは極を持つケースをそれぞれ考えると4種類に分かれることがようやく見えてきた。 その前に零点と極の位置関係や大小関係や零点の近傍で微係数が正であるかどうかが気になる。 このあたりがFoster Reactance Theoremで最も重要な部分であるが、ほとんどの書では結論だけが示されていて導出過程についてはほとんど触れられていないか天下りな説明になっている。当時のFosterの論文はBell研のジャーナルに掲載されていたので一般には公開されていない(戦前限られた研究機関や大学にしか配布されていなかった)し、あったとしてもベル研が無くなった今では廃棄処分されてもう手に入らないだろう。 こうなったらFosterの偉業を追体験するしかあるまい。 先に駆動点インピーダンスの式を見る限り、零点と極の出現順序は式上は任意であるように見える。しかし本当にそうだろうか? 前出の駆動点インピーダンスの式はLとCのみからなるリアクタンス関数であるが、リアクタンス関数は奇関数であることを確かめてみよう。 奇関数の定義から Z(-s)=-Z(s) が成り立つ必要がある。リアクタンス関数の式にsの代わりに-sを代入すると ということになり奇関数であることが証明された。 次ぎなる問題は零点と極の数について。 リアクタンス関数が正実関数であるためには、分子と分母の多項式の次数の差がたかだか1でなければならないことは既に学んだ通り。そのことから、リアクタンス関数の式で分子の項(零点に対応)と分母の項(極に対応)の数は同数でなければならないことになる。従ってリアクタンス関数の零点と極の数はω=0を除いては同数でなければならないことになる。またω=0を除いて零点及び極は互いに共役な複素数で虚軸上にのみ対で現れることになるのも明らか。 すると零点と極は虚軸上にどのような順番で現れるのかというのが疑問として残る。 ある本では天下り的に、別の本ではいくつかの回路例で定性的に零点と極が交互に現れるとしているが一般的になぜそういえるのか? それにはまず先のリアクタンス関数の式でs=jωとしてみる必要がある ω=0に極をもつケースは 一方ω=0に零点を持つケースは ということになる。 ここでもし 例えば というようなリアクタンス関数を考えてみると、これをω=0とω=1の間でプロットしてみると wxplot2d([-((2-o^2)*(3-o^2))/((1-o^2)*o)], [o,0.01,0.99])$ 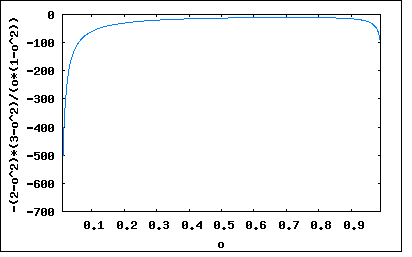 という具合に一端はインピーダンス値が増加するものの途中で減少し-∞へ逆戻りしてしまう。こんな周波数特性をもった回路は受動素子だけでは実現できない。 同じ式を部分分数に展開すると (%i19) (s^2+2)*(s^2+3)/(s*(s^2+1)); (%o19) ((s^2+2)*(s^2+3))/(s*(s^2+1)) (%i20) partfrac(((s^2+2)*(s^2+3))/(s*(s^2+1)), s); (%o20) -(2*s)/(s^2+1)+s+6/s すなわち ということになり、負の留数を持つためこれは正実関数ではないということになる。 一方零点と極が交互に現れる以下のような関数では ω=0からω=1.4の近傍をプロットしてみると、ω=1に零点が現れて極(ω=2)に向かって増加しているのがわかる。 wxplot2d([-((1-o^2)*(3-o^2))/((2-o^2)*o)], [o,0.1,1.4])$ 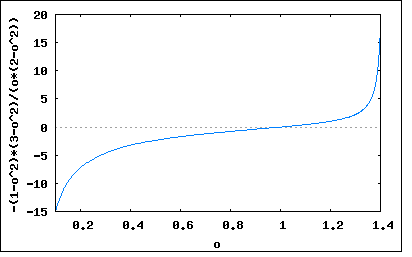 同様に部分分数に展開してみると (%i21) partfrac(((s^2+1)*(s^2+3))/(s*(s^2+2)), s); (%o21) s/(2*(s^2+2))+s+3/(2*s) すなわち 留数はすべて正の値をとるため正実関数である。 この辺を厳密に数学的に説明もしくは証明するのは他書に譲るとして、ここでは定性的に零点と極は1位孤立で交互に現れなければ正実関数でないとする、すなわち ということになる。 ここで 同様に先ほど疑問の生じたω=∞の時にリアクタンス関数はどうなるかという点。 ω=0に極を持つケースでは、 ω=0に零点を持つケースでは、 どちらのケースでも分子の次数が分母の次数より1大きいので、ω=∞ではZ=∞となる。従ってω=∞は極ということになる。 しかし ω=0を極としω=∞を零点とするケースでは、 これがIQが低い者にとってはピンとこない。わかってしまえば、なんだあたりまえじゃないか(´∀` )という笑い話になるのだが。 同様にω=0とω=∞の両方に零点を持つケースでは、 ということになる。 これでようやく下記4つのケースに分かれることが納得いく。 これで色々な本に書いてあることが理解できるようになった。 いくらどの本にも同じことが書いてあっても、偉い先生が書いたものであっても、自分が納得いかない限り理解したとは言えないわけで。自分なりに納得がいく理解が得られれば、著者によっていろいろ表現や表記が違っていても同じことを書いているということをようやく理解できるわけである。IQが高い者なら一冊読むだけですべてを瞬時に理解してしまうかもしれないが、IQが低いものにとってはそれはそれは時間が必要である。誰か理解している人が側に入れば幸いかというとそうでもない。誰も教えてくれる人が居ない方が自ら切り開く力が備わるのである。先端に到達するともう後ろにも前にも自分よりも知っている人は誰もいなくなるわけで、そのときに自ら切り開く力が初めて問われる。 さて話を本流に戻そう。まだ終わっていない。 零点の近傍での虚軸に対する微係数が正であることを確かめなければならない。これには何度も登場する駆動点インピーダンス(リアクタンス関数)の式を部分分数に分解してωで微分してみる必要がある。 当初それをやってみた結果を書いたのだが間違いに気づいてすぐ消してしまった。その間違いの原因を知るのに結構時間を要した。なにしろ多項式の有理関数の部分分数展開なんてのは、ヘビサイドが展開定理を発見するまで数学者は誰も知らなかったわけだし。まあ、多項式を多項式で割ると商と余りが出るのはみんな知っていたわけだけど、その余りの部分はヘビサイドが展開定理を見いだすまで余りのまま(多項式の有理式のまま)だった。そんなばかなと思うけど、それが歴史上の事実なのだ。ヘビサイドは数学的に証明したわけではなくそれを演算子法と併せて伝送路の過渡応答解析のための微分方程式を解くためにそれを用いた、それが厳密に数学で証明されるには後の群論とか抽象代数学の発達を待つ必要があった。 べき級数の多項式の有理関数は、同一基数の数同志の割り算と同形であることに気づく必要がある。 2端子回路(一端子対回路)に関する参考書はどれも最初に導出した駆動点インピーダンスの式が以下の様な部分分数に展開できるとしか書いていない。 分数が理解できないわけではないが、最初に自分で駆動点インピーダンスの式を部分分数に展開しようと試みた際に過ちを侵した時に一連の疑問が生じた。 手元の共立出版の「数学公式」には"8. 分数"の章に以下の様な部分分数展開の公式が載っている。 引用:
これはまさにヘビサイドの展開定理そのものであるのだが、これに基づいて駆動点インピーダンスの式を部分分数展開しようとしたのが問題だった。良く見れば、この展開定理は分子の多項式の次数が分母の多項式の次数よりも低いことが前提である。今回の駆動点インピーダンスの式は分子の方が分母よりも次数が1つ高いので、そのまま使うと誤った結果を招いてしまう。 それでは分子の次数が分母の次数よりも高い場合にはどうすればいいのか、公式集のその章にはそのケースについては書かれていない。では多項式の一般的な割り算(除法)はどうなっているのかというと、これはずっと後の"J. 整数論"という章に 引用:
と書いてあるだけである。所謂割り算の商(q)と余り(r)についての話であるが、部分分数展開の定理もEuclidの互除法に続いて書いてある以下の定理群から自明であるとも感じ取られる。 引用:
実は多項式と分数の関係は歴史が古く、数学史の中でも古代から存在しているのと、既に現在では"終わった"領域であるという点である。従って最も古い古典数学とも言える。しかし数学の発展上欠くことができないのは言うまでもない。多項式は方程式の解法という問題と密接に絡んでいるし、様々の基数の数の表現はまさに多項式そのものである。複素解析に至っては多公式の分数で表される有理型関数が重要な振る舞いをするのは回路網合成理論でも同じこと。 なぜそれだけ重要な様々な分野で同時発生している数学的な対象がまともに関連づけて体系的に説明されていないのかが疑問として出てくる。数学は蟻の巣穴のようで様々な意図で別々の場所から掘り進んだ穴が偶然かもしくは起こるべくして起こるように一カ所でつながるということはあり得るが、およそ多項式と分数については、時空を通り越して別空間でまったく離れた場所でつながりあっているようにしか見えない。それを納得いくように理解するには自分で理論を再構成するしかない。 実際にいろいろ調べてみると、部分分数展開については、やはりそれが登場する複素解析の有理型関数の積分のところで、著名なテキストではそれぞれ著者が独自に再構成した証明や導出手順を載せているのを見つけることができる。代数学では単に最新の抽象代数理論でEuclidの互除法の定義を再構成しているだけにすぎない。従って代数学の本を読んでもわからないわけである。 手元にある「A COURSE OF MODERN ANALYSIS」では"5.64 Functions with the essential singularities"に、Liouville's Theoremによって孤立特異点を持つ有理型一変数複素関数が以下の式で表されることを導いている。 また代数的整数論講義とかの著者で知られる高木貞治の「解析概論」の"66. 有理関数の積分の理論"でも独自の構成で有理関数 がαをf(z)のk次の極であるとすると、f(z)の主要部が(z-α)^kf(z)のαにおけるTaylor展開の最初のk項 を(z-α)^kで割って が得られるのでφ(z)をψ(z)で割った商をQ(z)、剰余をφ0(z)とすれば で表されることを示している。これらは同一の結論に至る、それぞれの著者が納得している解釈を示しているに過ぎず厳密な証明にはなっていない。おそらく自明だし、部分分数分解は数学的にも"終わった"話なのでこの程度の説明で十分だろうと思っている節がある。 厳密な証明の形をした最も数学者的な部分分数展開の定義は共立出版から現在出版されている「代数方程式のガロア理論」"Galois'Theory of Algebraic Equation" Jean-Pierre Tignol著にある"第5章 多項式の現代的解釈"の"付録:有理式の部分分数への分解"が最も厳密で現代的な形をしている。元々は大学生向けの講義内容であるが、代数方程式の歴史を紀元前2000年に既に分数を扱っていたバビロニア人の粘土板の記述からはじまる話は一般人にも面白く読める。インターネットでも分数で検索するとエジプト人が同様に分数を扱っていて建築物や構造物がすべて分数で表されることを知っていたらしいことがわかる。合理的な分数で表すことのできない不合理な無理数を発見した人物が謀殺された話とかは驚きである。これらを読んで、ようやく部分分数展開の定理がEuclidの互除法から導くことが出来るというのを確認した次第である。 既に歴史上忘れ去られようとしているリアクタンス関数がこんなにも長い議論を招くとは思っても見なかったが、ようやくここまでたどり着いた感じがする。 結論を言うと、最初侵した間違いというのは商を考えていなかったという点である。分子の次数が分母の次数より1高い場合には一次式が商として現れるのである。これが駆動点インピーダンスがω=∞で極を持つためには無くてはならない点だったということである。言うなれば常識なのだが。今の小学生は二学年で分数を習うらしい。昔は確か4学年と中途半端な時に習ったので、良く憶えていないし、学生になってからもちょっと自信が無かった憶えがある。 分数はおそらく人類が暦や時間の概念を使い経済活動を始めたのと同時進行で考案された数学であると思われる。それだけに歴史が古い。数学専攻の学生は代数学でこうした古い数の概念を抽象理論で再構成しおさらいすることになるが、これがまた難しい。本当は小学二年生でそうした数への疑問を持てば、天才的な数学者が現れるかもしれないが、天下り的に教えるので、さっぱり憶えないという弊害があるかもしれない。やはり学ぶモチベーションを高めるのは自分が納得が行かない疑問を追求することが一番である。 さてなんの話だったっけ。 あ、そうだ駆動点インピーダンス関数の零点の近傍における微係数が正であることを証明しないといけない。そのために部分分数展開の話に迷い込んだのである。 ここでようやく以下の様に展開された駆動点インピーダンスの式の導関数を求めることになる。 ここでs=jωを代入すると であることが自明である。 これらがFoster's Reactance Theoremである。 著者はたった数行に要約しているだけだが、それだけではなんのことかさっぱりわからないのである。今日的にはこの理論はあまり活躍する機会が無い、というのも損失の無いLとCだけの回路というのが理想的すぎるので現実の素子の損失係数が無視できる低周波領域のみに適用範囲が絞られるのと、低周波領域では能動素子を使ったアクティブフィルタ回路かデジタル信号処理によるデジタルフィルタが今日の設計の主流であるためである、アナログフィルタの基礎を知るには後のCauerの損失を含む合成理論を学ぶ必要がある。今日でも高周波回路では未だに受動素子のみから成るフィルター回路が使われる。高周波のフロントエンドなど低損失かつ低ノイズが要求される部分は依然としてパッシブフィルタしか選択肢が無い。デジタルフィルタではサンプリング速度が追いつかないしノイズを発生する。マイクロ波とかではなおさらである。それでも基本の出発点はここにある。すっ飛ばして今日的なフィルタ理論とか先へ進んでも良いが、それらはFoster理論を理解していることを前提としているので、最後はここに戻って来ることになる。 P.S 賢明な読者であれば、複素解析理論の有理型関数の部分分数展開とヘビサイドの展開定理、それにFoster展開に関してmissing linkがあることに気づくであろう。Foster展開の分母が二次式である項は以下の様に共役複素数からなる2つの部分分数に更に分解されるはずである。この議論については次ぎのFoster展開で詳しく扱うことにする。 |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| |
webadm | 2009-10-15 7:06 |
| |
webadm | 2009-10-15 19:22 |
| |
webadm | 2009-10-15 21:47 |
| |
webadm | 2009-10-16 1:11 |
| » |
webadm | 2009-10-22 7:47 |
| |
webadm | 2009-11-11 19:00 |
| |
webadm | 2009-11-12 1:04 |
| |
webadm | 2009-12-20 2:36 |
| |
webadm | 2009-12-2 4:14 |
| |
webadm | 2009-12-24 19:18 |
| |
webadm | 2009-12-25 18:57 |
| |
webadm | 2009-12-25 21:21 |
| 投稿するにはまず登録を | |

