Gan's blog - フォーラム

メイン > > 電気回路理論おもちゃ箱 > 2端子対回路演習問題

投稿者	スレッド
webadm	投稿日時: 2010-5-23 17:58
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3087	Zobel変換次ぎの問題は今まで登場してきたT形回路とπ形回路をそれぞれ等価変換(Zobel変換）する問題。ただしL1C1=L2C3が成り立つものとする。これも以前の問題の結果を利用して著者とは別解でやってみよう。最初に見通しがよくなるようにT形回路とπ形回路を以下のように表す。 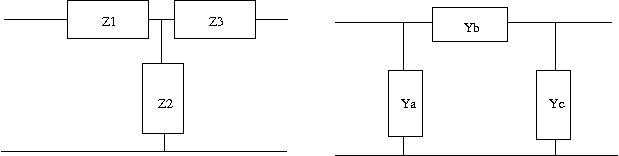T形回路のインピーダンス行列は以前の問題の解より $\begin{eqnarray}<br />\left[\begin{array}<br />Z_{11} & Z_{12}\\<br />Z_{21} & Z_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />Z_1+Z_2 & Z_2\\<br />Z_2 & Z_2+Z_3<br />\end{array}\right]<br />\end{eqnarray}$ 同様にπ形回路のアドミッタンス行列も以前の問題の解より $\begin{eqnarray}<br />\left[\begin{array}<br />Y_{11} & Y_{12}\\<br />Y_{21} & Y_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />Y_a+Y_b & -Y_b\\<br />-Y_b & Y_b+Y_c<br />\end{array}\right]<br />\end{eqnarray}$ 一方各回路をそれぞれのパラメータで表すと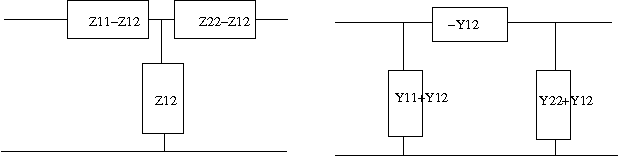次にT形回路のアドミッタンス行列をZ1,Z2,Z3で表すと $\begin{eqnarray}<br />\left[\begin{array}<br />Y_{11} & Y_{12}\\<br />Y_{21} & Y_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />Z_{11} & Z_{12}\\<br />Z_{21} & Z_{22}<br />\end{array}\right]^{-1}\\<br />&=&\left[\begin{array}<br />Z_1+Z_2 & Z_2\\<br />Z_2 & Z_2+Z_3<br />\end{array}\right]^{-1}\\<br />&=&\left[\begin{array}<br />\frac{Z_2+Z_3}{Z_1 Z_2+Z_2 Z_3+Z_1 Z_3} & -\frac{Z_2}{Z_1 Z_2+Z_2 Z_3+Z_1 Z_3}\\<br />-\frac{Z_2}{Z_1 Z_2+Z_2 Z_3+Z_1 Z_3} & \frac{Z_1+Z_2}{Z_1 Z_2+Z_2 Z_3+Z_1 Z_3}<br />\end{array}\right]<br />\end{eqnarray}$ 従ってπ形回路のYa,Yb,Ycを等価なT形回路のZ1,Z2,Z3で表すと $\begin{eqnarray}<br />Y_a&=&Y_{11}+Y_{12}\\<br />&=&\frac{Z_3}{Z_1 Z_2+Z_2 Z_3+Z_1 Z_3}\\<br />Y_b&=&-Y_{12}\\<br />&=&\frac{Z_2}{Z_1 Z_2+Z_2 Z_3+Z_1 Z_3}\\<br />Y_c&=&Y_{22}+Y_{12}\\<br />&=&\frac{Z_1}{Z_1 Z_2+Z_2 Z_3+Z_1 Z_3}<br />\end{eqnarray}$ ここで題意よりT形回路のZ1,Z2,Z3は $\begin{eqnarray}<br />Z_1&=&\frac{1}{j\omega C_1+\frac{1}{j\omega L_1}}\\<br />&=&\frac{j\omega L_1}{1-{\omega}^2 L_1 C_1}\\<br />Z_2&=&j\omega L_2\\<br />Z_3&=&\frac{1}{j\omega C_3}\\<br />&=&-\frac{j}{\omega C_3}<br />\end{eqnarray}$ これを先のYa,Yb,Ycの式にそれぞれ代入するとL1C1=L2C3が成り立つ場合 $\begin{eqnarray}<br />Y_a&=&\frac{Z_3}{Z_1 Z_2+Z_2 Z_3+Z_1 Z_3}\\<br />&=&-\frac{j}{\omega C_3\left(-\frac{{\omega}^2L_1 L_2}{1-{\omega}^2L_1 C_1}+\frac{L_2}{C_3}+\frac{L_1}{C_3\left(1-{\omega}^2L_1 C_1\right)}\right)}\\<br />&=&-\frac{j\cancel{\left({\omega}^2L_1 C_1-1\right)}}{\omega\left(L_1\cancel{\left({\omega}^2L_2 C_3-1\right)}+L_2\cancel{\left({\omega}^2L_1 C_1-1\right)}\right)}\\<br />&=&-\frac{j}{\omega\left(L_1+L_2\right)}\\<br />Y_b&=&\frac{Z_2}{Z_1 Z_2+Z_2 Z_3+Z_1 Z_3}\\<br />&=&\frac{j\omega L_2}{-\frac{{\omega}^2L_1 L_2}{1-{\omega}^2L_1 C_1}+\frac{L_2}{C_3}+\frac{L_1}{C_3\left(1-{\omega}^2L_1 C_1\right)}}\\<br />&=&\frac{j\omega L_2 C_3\cancel{\left({\omega}^2L_1 C_1-1\right)}}{L_1\cancel{\left({\omega}^2L_2 C_3-1\right)}+L_2\cancel{\left({\omega}^2L_1 C_1-1\right)}}\\<br />&=&\frac{j\omega L_2 C_3}{L_1+L_2}\\<br />Y_c&=&\frac{Z_1}{Z_1 Z_2+Z_2 Z_3+Z_1 Z_3}\\<br />&=&\frac{j\omega L_1}{\left(1-{\omega}^2L_1 C_1\right)\left(-\frac{{\omega}^2L_1 L_2}{1-{\omega}^2L_1 C_1}+\frac{L_2}{C_3}+\frac{L_1}{C_3\left(1-{\omega}^2L_1 C_1\right)}\right)}\\<br />&=&-\frac{j\omega L_1 C_3}{L_1\left({\omega}^2L_2 C_3-1\right)+L_2\left({\omega}^2L_1 C_1-1\right)}\\<br />&=&-\frac{j\omega L_1 C_3}{\left(L_1+L_2\right)\left({\omega}^2L_1 C_1-1\right)}<br />\end{eqnarray}$ 従って等価なπ形回路は $\begin{eqnarray}<br />Z_a&=&\frac{1}{Y_a}\\<br />&=&-\frac{1}{\frac{j}{\omega\left(L_1+L_2\right)}}\\<br />&=&j\omega\left(L_1+L_2\right)\\<br />&=&j\omega L_a\\<br />L_a&=&L_1+L_2\\<br />Z_b&=&\frac{1}{Y_b}\\<br />&=&\frac{1}{\frac{j\omega L_2 C_3}{L_1+L_2}}\\<br />&=&-\frac{j\left(L_1+L_2\right)}{\omega\left(L_2 C_3\right)}\\<br />&=&\frac{1}{j\omega\left(\frac{L_2 C_3}{L_1+L_2}\right)}\\<br />&=&\frac{1}{j\omega C_b}\\<br />C_b&=&\frac{L_2 C_3}{L_1+L_2}=\frac{C_3}{\frac{L_1}{L_2}+1}=\frac{C_3}{\frac{C_3}{C_1}+1}=\frac{C_1 C_3}{C_1+C_3}\\<br />Z_c&=&\frac{1}{Y_c}\\<br />&=&-\frac{1}{\frac{j\omega L_1 C_3}{\left(L_1+L_2\right)\left({\omega}^2L_1 C_1-1\right)}}\\<br />&=&-\frac{\left(L_1+L_2\right)\left({\omega}^2L_1 C_1-1\right)}{j\omega L_1 C_3}\\<br />&=&\frac{L_1+L_2}{j\omega L_1 C_3}-\frac{\left(L_1+L_2\right){\omega}^2\cancel{L_1} C_1}{j\omega \cancel{L_1} C_3}\\<br />&=&\frac{1}{j\omega\left(\frac{L_1 C_3}{L_1+L_2}\right)}+j\omega\frac{\left(L_1+L_2\right)C_1}{C_3}\\<br />&=&\frac{1}{j\omega C_c}+j\omega L_c\\<br />C_c&=&\frac{L_1 C_3}{L_1+L_2}=\frac{C_3}{1+\frac{L_2}{L_1}}=\frac{C_3}{1+\frac{C_1}{C_3}}=\frac{{C_3}^2}{C_1+C_3}\\<br />L_c&=&\frac{\left(L_1+L_2\right)C_1}{C_3}=\frac{\left(L_1+L_2\right)L_2}{L_1}<br />\end{eqnarray}$ ということになる。今度は逆にπ形回路のインピーダンス行列をYa,Yb,Ycで表すと $\begin{eqnarray}<br />\left[\begin{array}<br />Z_{11} & Z_{12}\\<br />Z_{21} & Z_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />Y_{11} & Y_{12}\\<br />Y_{21} & Y_{22}<br />\end{array}\right]^{-1}\\<br />&=&\left[\begin{array}<br />Y_a+Y_b & -Y_b\\<br />-Y_b & Y_b+Y_c<br />\end{array}\right]^{-1}\\<br />&=&\left[\begin{array}<br />\frac{Y_c+Y_b}{Y_a Y_b+Y_a Y_c+Y_b Y_c} & \frac{Y_b}{Y_a Y_b+Y_a Y_c+Y_b Y_c}\\<br />\frac{Y_b}{Y_a Y_b+Y_a Y_c+Y_b Y_c} & \frac{Y_a+Y_b}{Y_a Y_b+Y_a Y_c+Y_b Y_c}<br />\end{array}\right]<br />\end{eqnarray}$ 従ってT形回路のインピーダンスZ1,Z2,Z3をπ形回路のYa,Yb,Ycで表すと $\begin{eqnarray}<br />Z_1&=&Z_{11}-Z_{12}\\<br />&=&\frac{Y_c}{Y_a Y_b+Y_a Y_c+Y_b Y_c}\\<br />Z_2&=&Z_{12}\\<br />&=&\frac{Y_b}{Y_a Y_b+Y_a Y_c+Y_b Y_c}\\<br />Z_3&=&Z_{22}-Z_{12}\\<br />&=&\frac{Y_a}{Y_a Y_b+Y_a Y_c+Y_b Y_c}<br />\end{eqnarray}$ 題意よりπ形回路のYa,Yb,Ycは $\begin{eqnarray}<br />Y_a&=&\frac{1}{j\omega L_1+\frac{1}{j\omega C_1}}\\<br />&=&\frac{j\omega C_1}{1-{\omega}^2L_1 C_1}\\<br />Y_b&=&\frac{1}{j\omega L_2}\\<br />&=&-\frac{j}{\omega L_2}\\<br />Y_c&=&j\omega C_3<br />\end{eqnarray}$ これを先のZ1,Z2,Z3の式に代入するとL1C1=L2C3が成り立つ場合 $\begin{eqnarray}<br />Z_1&=&\frac{Y_c}{Y_a Y_b+Y_a Y_c+Y_b Y_c}\\<br />&=&\frac{j\omega C_3}{\frac{C_1}{L_2\left(1-{\omega}^2L_1 C_1\right)+\frac{C_3}{L_2}-\frac{{\omega}^2C_1 C_3}{1-{\omega}^2L_1 C_1}}}\\<br />&=&\frac{j\omega L_2 C_3\cancel{\left({\omega}^2L_1 C_1-1\right)}}{C_1\cancel{\left({\omega}^2L_2 C_3-1\right)}+C_3\cancel{\left({\omega}^2L_1 C_1-1\right)}}\\<br />&=&\frac{j\omega L_2 C_3}{C_1+C_3}\\<br />&=&j\omega L^{\'}_1\\<br />L^{\'}_1&=&\frac{L_2 C_3}{C_1+C_3}=\frac{L_2}{\frac{C_1}{C_3}+1}=\frac{L_2}{\frac{L_2}{L_1}+1}=\frac{L_1 L_2}{L_1+L_2}\\<br />Z_2&=&\frac{Y_b}{Y_a Y_b+Y_a Y_c+Y_b Y_c}\\<br />&=&-\frac{j}{\omega L_2\left(\frac{C_1}{L_2\left(1-{\omega}^2L_1 C_1\right)}+\frac{C_3}{L_2}-\frac{{\omega}^2C_1 C_3}{1-{\omega}^2L_1 C_1}\right)}\\<br />&=&-\frac{j\cancel{\left({\omega}^2L_1 C_1-1\right)}}{\omega\left(C_1\cancel{\left({\omega}^2L_2 C_3-1\right)}+C_3\cancel{\left({\omega}^2L_1 C_1-1\right)}\right)}\\<br />&=&-\frac{j}{\omega\left(C_1+C_3\right)}\\<br />&=&\frac{1}{j\omega C^{\'}_2}\\<br />C^{\'}_2&=&C_1+C_3\\<br />Z_3&=&\frac{Y_a}{Y_a Y_b+Y_a Y_c+Y_b Y_c}\\<br />&=&\frac{j\omega C_1}{\left(1-{\omega}^2L_1 C_1\right)\left(\frac{C_1}{L_2\left(1-{\omega}^2L_1 C_1\right)}+\frac{C_3}{L_2}-\frac{{\omega}^2C_1 C_3}{1-{\omega}^2L_1 C_1}\right)}\\<br />&=&-\frac{j\omega L_2 C_1}{C_1\left({\omega}^2L_2 C_3-1\right)+C_3\left({\omega}^2L_1 C_1-1\right)}\\<br />&=&-\frac{j\omega L_2 C_1}{\left(C_1+C_3\right)\left({\omega}^2L_1 C_1-1\right)}\\<br />&=&\frac{1}{\left(C_1+C_3\right)\left(j\omega\frac{L_1}{L_2}+\frac{1}{j\omega L_2 C_1}\right)}\\<br />&=&\frac{1}{j\omega\frac{L_1\left(C_1+C_3\right)}{L_2}+\frac{C_1+C_3}{j\omega L_2 C_1}}\\<br />&=&\frac{1}{j\omega C^{\'}_3+\frac{1}{j\omega L^{\'}_3}}\\<br />C^{\'}_3&=&\frac{L_1\left(C_1+C_3\right)}{L_2}=\frac{C_3\left(C_1+C_3\right)}{C_1}\\<br />L^{\'}_3&=&\frac{L_2 C_1}{C_1+C_3}=\frac{L_2}{1+\frac{C_3}{C_1}}=\frac{L_2}{1+\frac{L_1}{L_2}}=\frac{{L_2}^2}{L_1+L_2}<br />\end{eqnarray}$ ということになる。ちなみにC'3の値が著者の解答とは違っているが、こちらが正しい。著者の解はL2/L1をL1/L2と転記ミスしている。それぞれ回路図に表すと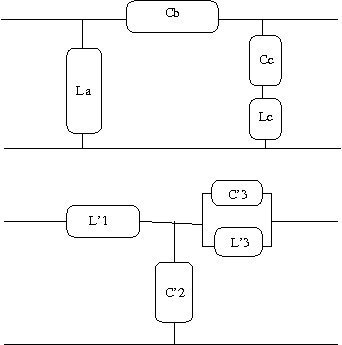と言う結果になる。 P.S. ふう、ほとんどが計算で大変だった。最初T形回路とπ形回路の素子定数の添字を一緒にして混乱したので、改めてπ形回路由来はa,b,cでT形回路由来は1,2,3とした。途中の式の操作はMaximaを使って確認するも、入力ミスがあったりして更に頭が混乱してしまった。最後に著者の解答に驚愕の誤記があるというどんでん返しで寝込むかと思った。結局CならCだけから、LならLだけから成るように式を整えるのは人間が意図的にやらないとどうしようもなかった。そういえばZobel変換というのは検索してもまったくひっかからない。おそらくΔ-Y等価変換と同じだと思われるが、Valkenburgによると1899年に既にA.E.KennelyがElectric World and Engineering誌の記事"The equivalence of triangles and three-point stars in conducting networks"で示しているのでZobel由来と言う人はほとんど居ないのだろう。Zobelが二端子対回路で同じことを示したのはそれからずっと後のことだし。

フラット表示

前のトピック | 次のトピック

題名	投稿者	日時
2端子対回路演習問題	webadm	2010-5-20 4:53
インピーダンスパラメータ	webadm	2010-5-20 5:54
インピーダンスパラメータとアドミッタンスパラメータ	webadm	2010-5-22 23:43
インピーダンスパラメータとハイブリッドパラメータ	webadm	2010-5-23 1:32
インピーダンス行列とアドミッタンス行列	webadm	2010-5-23 10:12
T形回路	webadm	2010-5-23 16:25
続：T形回路	webadm	2010-5-23 16:33
π形回路	webadm	2010-5-23 17:20
» Zobel変換	webadm	2010-5-23 17:58
ハイブリッドパラメータ	webadm	2010-5-24 17:53
アドミッタンスパラメータと４端子定数	webadm	2010-5-26 11:41
伝送行列	webadm	2010-5-26 14:34
T形回路の伝送行列	webadm	2010-5-26 15:14
4端子定数	webadm	2010-5-27 3:18
続：伝送行列	webadm	2010-5-27 13:50
続：４端子定数	webadm	2010-5-27 22:14
続々：４端子定数	webadm	2010-5-29 3:39
インピーダンス行列	webadm	2010-5-29 11:27
アドミッタンス行列	webadm	2010-5-29 11:57
またまた：４端子定数	webadm	2010-5-30 11:15
二端子対回路の並列接続	webadm	2010-5-30 12:37
もうひとつの：４端子定数	webadm	2010-5-30 12:45
アドミッタンスパラメータ	webadm	2010-6-3 12:42
まだまだ：４端子定数	webadm	2010-6-5 13:04
影像パラメータと４端子定数	webadm	2010-6-5 13:44
影像パラメータ	webadm	2010-6-12 22:30
続：影像パラメータ	webadm	2010-6-13 5:07
続々：影像パラメータ	webadm	2010-6-17 5:13
影像インピーダンス	webadm	2010-6-17 16:21
続：影像インピーダンス	webadm	2010-6-17 19:40
まだまだ：影像パラメータ	webadm	2010-6-22 18:50
もうひとつの：影像パラメータ	webadm	2010-6-25 21:54
４端子定数と影像インピーダンス	webadm	2010-6-26 0:45
インピーダンス整合	webadm	2010-6-26 11:27
もうひとつの：影像インピーダンス	webadm	2010-6-26 21:55
反復インピーダンスと４端子定数	webadm	2010-6-27 0:05
反復パラメータ	webadm	2010-6-28 21:04
影像インピーダンスと反復インピーダンス	webadm	2010-6-29 18:16
π形回路の伝送行列、影像パラメータ、反復パラメータ	webadm	2010-7-8 21:06
相互誘導回路と理想変成器	webadm	2010-7-28 6:11
Norton変換	webadm	2010-8-17 10:44
続：Norton変換	webadm	2010-8-17 20:48
容量性変成器	webadm	2010-8-18 3:42
抵抗性変成器	webadm	2010-8-21 10:11
理想ジャイレーター	webadm	2010-10-31 3:26
続：理想ジャイレータ	webadm	2010-11-19 2:41
続々：ジャイレータ	webadm	2010-11-23 21:29
対称回路	webadm	2010-11-25 9:18
続：対称回路	webadm	2010-11-30 0:01
続々：対称回路	webadm	2010-11-30 9:27
またまた：対称回路	webadm	2010-11-30 23:28
軸対称二端子対回路	webadm	2010-12-3 8:26
一方向性回路	webadm	2010-12-8 9:13
続：一方向性回路	webadm	2010-12-8 10:37
Zパラメータ	webadm	2010-12-9 22:51
続：Zパラメータ	webadm	2010-12-10 0:17
４端子定数	webadm	2010-12-14 6:51
理想オペアンプ	webadm	2010-12-14 7:03
続々：Zパラメータ	webadm	2010-12-20 10:10
reactance回路	webadm	2010-12-20 22:52
全域通過回路	webadm	2010-12-23 13:53
最小位相推移回路	webadm	2010-12-23 21:54
続：最小位相推移回路	webadm	2011-4-22 7:02
続々：最小位相推移回路	webadm	2011-4-22 9:38

投稿するにはまず登録を