| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2011-6-10 5:50 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
複合フィルタ(composite filter) フィルタの章に関してはこれまでメインテキストとしていた「詳解 電気回路演習(下)」に代えて、M. E. VAN VALKENBURGの半世紀前の著書「NETWORK ANALYSIS」の"CHAPTER 13, TWO-TERMINAL-PAIR REACTIVE NETWORKS(FILTERS)"をテキストとして学ばさせて頂いている。前者のフィルタの章は他の電気回路本と同様に逆L字回路での解析結果だけを示すだけでその導出については触れられていない。
今日的には古典フィルタを設計する機会は少ないかもしれないが、先人はここから学んできているため、近代のフィルタ理論もそうしたバックグラウンドがあってこそ優位点を理解できるはずである。 古典フィルタの定K形、誘導M形はどちらも特性に一長一短があるが、2種類を併用すると互いの長所が互いの欠点を補い合う、また誘導M形の半回路(逆L字)を端に使用すると公称インピーダンスを持つ定抵抗で終端しても通過域でのインピーダンス不整合を最小にすることができる。従ってこれらの3種類の基本フィルタ回路を縦続接続することによる複合フィルタ(composite filter)設計をどうしても学ばないと意味が無い。 これまで結合フィルタと勝手に訳していたが、専門用語辞書を見るとどうやらcomposite filterの正式な訳は複合フィルタだったらしい。以前に書いた箇所をこっそり修正したのは内緒だ。 複合フィルタでは、これまで学んだ、 ・定K形フィルタ回路(T字、π形) ・定K形フィルタ半回路(T字の半回路、π形の半回路) ・誘導M形フィルタ回路(T字、π形) ・誘導M形フィルタ半回路(T字の半回路、π形の半回路) の8種をプロトタイプ(prototype)フィルタと呼び、それらを複数縦続接続してラダー形フィルタを構成する。 複合フィルタをこれらのプロトタイプフィルタを組み合わせて構成するために守るべきことは (1)それぞれのプロトタイプフィルタ間で映像インピーダンスが整合すること (2)それぞれのプロトタイプフィルタの減衰特性は目的とする複合フィルタ全体での減衰特性を満足するように選択すること の2点である。 具体例から考えよう。定K形プロトタイプフィルタをひとつと誘導M形プロトタイプフィルタをひとつを縦続接続した以下の様な低域通過フィルタを構成するものとする。 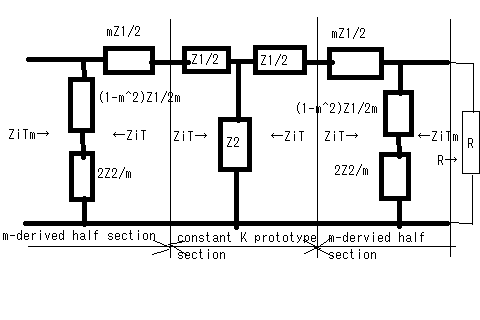 定K形プロトタイプが中央に、誘導M形プロトタイプは通過域でのインピーダンス整合をよくするためにT字回路を二分割して裏側を外向きに接続し、入出力端は公称インピーダンスRをもった定抵抗で終端できるようにする。プロトタイプフィルタ間は映像インピーダンス整合がとれている。入出力端が定抵抗終端なので厳密には整合がとれていないが、映像インピーダンスで終端した場合とおおよそ近い。x=ω/ω0に対してプロットすると 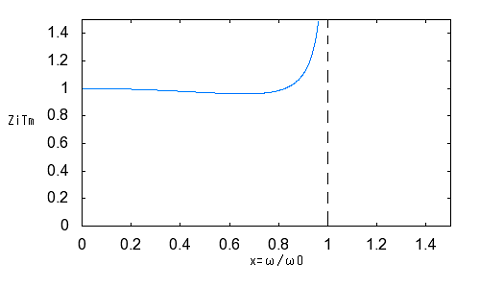 複合フィルタ全体での減衰定数は、それぞれのプロトタイプフィルタの減衰定数の和となる。 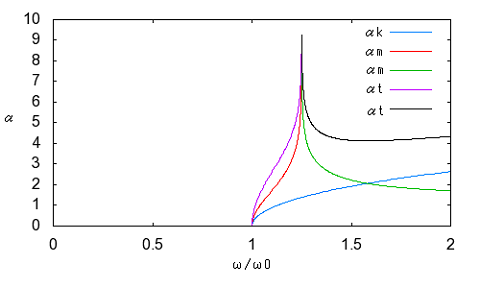 位相定数も同様に 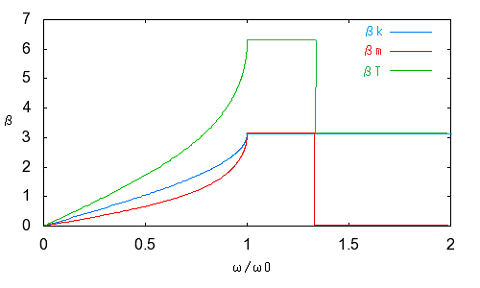 複合フィルタの入力インピーダンスと減衰特性は定K形フィルタや誘導M形フィルタ単独よりも凌いでいる。定K形フィルタと誘導M形フィルタのそれぞれの直列インピーダンスが共に減衰を強める方向に働くからである。 一部のケースでは、上の構成でも遮断周波数近辺での傾きが足らず十分な減衰特性が得られない場合がある。このケースでは2つ以上の誘導M形フィルタを映像インピーダンス整合と併せて使用する。回路図で表すと 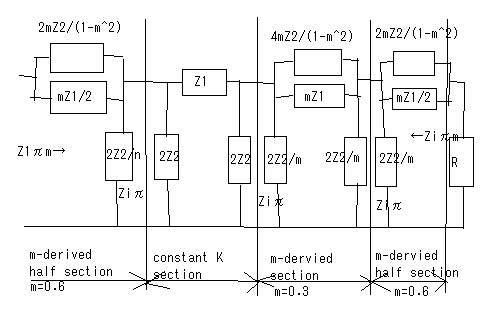 プロトタイプとなる定K形(π)フィルタとm=0.3の誘導M形(π)フィルタが中段に、初段と終段はm=0.6の誘導M形(π)を二分割した半回路をインピーダンス整合のために内向きに接続されている。 このフィルタの減衰定数はそれぞれのフィルタの減衰定数の総和となるので ということになる。同様に特性をプロットしてみると 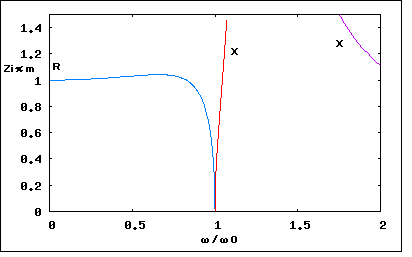 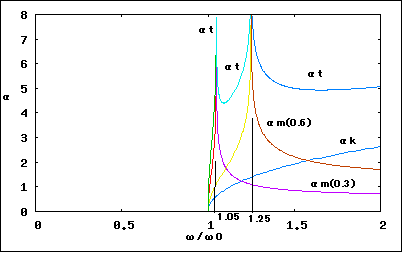 ということになる。位相定数に関してプロットするのは読者の課題としよう( ´∀`) 厳密には終段が映像インピーダンスではなく定抵抗Rで終端されているため、上記のプロットは映像インピーダンスで終端した場合の理想特性ということになる。 終端を定抵抗Rとすることによる影響については後ほど議論する。 ここまでの解析結果から複合フィルタの設計手法に関して (1)最初に、周波数の関数としての減衰定数に対する要求仕様を決めなければならない。減衰定数の仕様は以下の式の様に定K形フィルタと誘導M形フィルタのいくつかの組み合わせで満足される可能性がある。 ここでAは定K形回路の数、Bjは特定のmを持った誘導M形回路の数、nは異なるmの数である。通常、必要とされる定K形回路の数や誘導M形回路の数を決定する一意的な方法は無いので、試行錯誤が要求を満たす答えを得るのに必要とされる。 (2)定K形回路プロトタイプを選択し、素子定数を求める。この素子定数から、残りすべての誘導M形回路の素子定数を求める。 (3)少なくともm=0.6を持つひとつの誘導M形フィルタ回路をフィルタの初段と終段に入れる。これによって最適な映像インピーダンス特性が得られる。 (4)選択したプロトタイプのタイプと使用される回路の数は通常コスト面の配慮で制限される。 と言える。 終端の問題 定K形フィルタや誘導M形フィルタおよびそれらの半回路は互いに共通の映像インピーダンスで整合した形で接続することが出来る。しかしそれは前段と後段がそれぞれ映像インピーダンスで終端されることを前提としている。そうした映像インピーダンスと同じ特性を持つように複合フィルタの前後に接続される回路の入力インピーダンスや出力インピーダンスを設計することは困難である。一番簡単なのは定抵抗で終端することである。定K形フィルタや誘導M形フィルタの映像インピーダンスは で表される。xが0に近づくといずれもRに収束するのと、誘導M形ではm=0.6で通過域の映像インピーダンスがRとして近似出来ることから定抵抗終端の値Rは定K形フィルタの条件より で定まる。 Valkenburgは著書の注釈で、誘導M形π半回路ではRりも若干小さく、誘導M形T半回路ではRよりも若干大きくするとより良い近似となると書いている。その理由を考えるのは読者の課題としよう( ´∀`) 問題は定抵抗Rで以下の図の様にこれまで学んで来た複合フィルタを終端すると映像インピーダンスの前提が崩れてしまうのでこれまで議論してきた特性がどうなってしまうのだろうかという点である。 ここまでの理論では(1)回路中の素子値は乖離が無い、(2)互いに映像インピーダンスで整合している、ことを前提としてきた。実際の回路では素子は理想的なinductanceやcapacitanceから乖離して損失(抵抗)を伴う。その場合どうなのだろうか?また終端を映像インピーダンスではなく公称インピーダンスRで置き換えることによる影響は? 最初の疑問に関しては乖離が有限範囲にとどまる限りにおいて特性上の大きな乖離は生じないことが判っている(素子感度が低い、という)。たとえばinductanceの抵抗分によってQが低下しても15を超えるならば実用上許容範囲内である。実際に確かめるのは読者の課題としよう( ´∀`) 第二の疑問に関しては先の信号源と負荷の間にフィルタを挿入した場合にもたらされる損失、挿入損失(insertion loss)を定義する必要がある。挿入損失は以下の式で定義される。 ここでNは挿入損失で単位はネーパー、I2'は信号源に直接負荷を接続した場合に流れる電流、I2はフィルタを挿入した場合に負荷に流れる電流とする。挿入損失を数値計算する際に、I2'=I1とする。すなわち、信号源から流れ出す電流はフィルタを挿入してもしなくても変化ないものと仮定する。そうすると挿入損失は回路全体の電流伝達比から導くことができる。 最初に登場した複合フィルタを例に実際に挿入損失を計算しプロットしてみよう。 回路全体の伝送行列をFとすると、短絡電流伝達比は ということになる。 (2011/7/17) ふう、あっという間に一ヶ月以上間が開いてしまった。研究も勉強も進まなくても継続して考え続けることが大事で、一端まったく休止してしまうと休止する前に戻るのが億劫になる。毎日問題だけでも忘れないように記憶をリフレッシュする時間を作って後退だけはさせないようにすべきだ。 ここでValkenburgは誘導m型と定K形から成る同じ低域通過フィルタの両端を影像インピーダンスで終端した場合と、公称インピーダンス(R)で終端した場合の挿入損失のグラフをプロットして比較している。 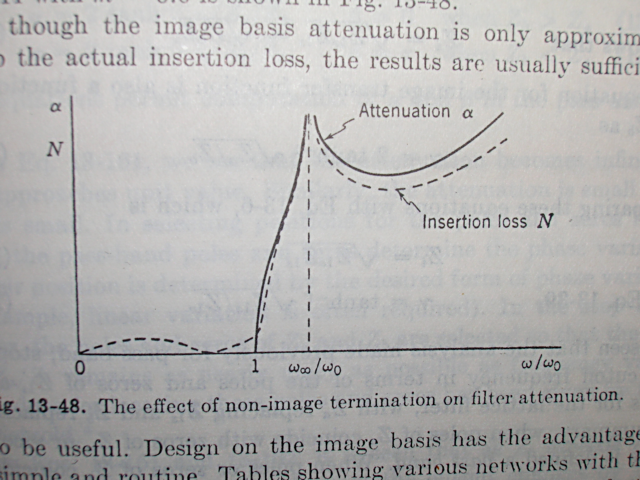 自分でプロットしてみると公称インピーダンスで終端した場合のプロットがValkenburgのと異なる点にだいぶ嵌ってしまっているためだ。 通過領域ではインピーダンス不整合によってわずかであるがリップルが生じている点は合っている。通過領域だけを拡大プロットし直してみると 確かにω/ω0=0.5あたりに減衰のピークがあり、その右に零点があって、今度は減衰ではなくゲインのピークが現れている。 ピークゲインが存在すること、減衰域での減衰定数と挿入損失との優劣関係が交代する周波数があることが、それらが無く挿入損失Nが全般的に減衰定数よりも特定的に劣化している(通過領域で挿入損失があり、阻止領域で挿入損失が減衰定数を下回ることを示している)Valkenburgのプロットとは異なっている。 全般的に公称インピーダンス(R)で複合フィルタの両端を終端しても特性として致命的な乖離が生じることは無いことがこれで確かめられる。 さてこのプロットの仕方が間違っているのか、それともValkenburgのプロットとやり方が違うのか釈然としない点が残る。おそらくValkenburgの執筆年代では計算機が無かったので、挿入損失の式の零点を求めて原点と途中の零点と極を結ぶ高次の曲線を雲形定規で適当に補間しながら描いたのではないかと思われる。 挿入損失Nのプロットに使用した式は、回路から伝送行列を求め、その短絡伝達係数Dの絶対値を対数変換したものを使用し、影像インピーダンスで終端した場合の減衰定数αは複合フィルタの両端に影像インピーダンスをシリーズに接続した対称二端子対回路の伝送行列の短絡伝達係数Dの絶対値を対数変換したものを使用した。式の導出およびプロットにはMaximaを使用した。読者自身で式をたててプロットしてみることを推奨するので、ここでは具体的な式は伏せておくことにしよう( ´∀`) 影像インピーダンスで両端を終端した場合の減衰定数αは複合フィルタの伝送行列の固有値の絶対値そのものである。Maximaで複合フィルタの伝送行列の固有値をMaximaで求めて、その絶対値の対数をプロットする方法でも同じ結果が得られた。実際に読者が手を使って確かめてみることを強く推奨する( ´∀`) グラフの極の数が1つの場合はまだ式が簡単だが、上の例にある誘導m形フィルタを二種類使ったものは式が複雑となり、Maximaでも簡単にはプロットできない。こちらはまだ逆双曲線関数を使ってプロットする方法が簡単である。昔の人は計算機こそもってなかったが知恵があった。 さすがにそれでも極や零点が複数ある楕円関数フィルターとなると手計算では困難となる。これらの応用は計算機の登場を待たねばならなかった。 |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| |
webadm | 2011-5-3 7:21 |
| |
webadm | 2011-5-4 9:24 |
| |
webadm | 2011-5-24 5:11 |
| |
webadm | 2011-6-1 5:49 |
| » |
webadm | 2011-6-10 5:50 |
| |
webadm | 2011-7-18 1:22 |
| 投稿するにはまず登録を | |

