| フラット表示 | 前のトピック | 次のトピック |
| 投稿者 | スレッド |
|---|---|
| webadm | 投稿日時: 2011-9-4 22:16 |
Webmaster   登録日: 2004-11-7 居住地: 投稿: 3113 |
続:3素子フィルタ 次の問題も3素子フィルタに関するもの。
上記の回路の遮断周波数をfl,fhとしたいとき、L,C1,C2をどのように選べばよいか、ただしf0=√(fl・fh)のときの終端抵抗をRとする。 というもの。一見すると前問の回路の逆回路のように思えるが、実は違う。前問の回路もそうだったが、定K形フィルタ回路から一素子(Lを)省いたような回路である。この話は昔Cauerの人となりと業績を紹介をした際に"従来知られているものよりもLがひとつ少なくてすむ"とかそのまま伝えられるまま書いた憶えがある。もしかしてそのことかもしれない。Cauerの著書や特許で出てきたものかもしれない。その追跡は読者の自由研究課題としよう( ´∀`) さて、問題であるが、題意が前問の逆問題である。今度は遮断周波数を与えられて、素子定数を求めるもの。同じようにはいかない。 ストラテジーとしては ・回路の影像インピーダンスから遮断周波数と素子定数の関係式を導く ・上記関係式と題意で与えられた条件から素子定数を解く というのが考えられる。と思ったらこれはすでに著者がやっている。 なので別のアプローチを考えよう。 ・回路の影像伝達定数から遮断周波数と素子定数の関係式を導く ・上記関係式と題意で与えられた条件から素子定数を解く というのをやってみよう。 影像インピーダンスと違って、影像伝達定数はどちらの方向でも同値なのでこちらの方が楽かもしれない。 回路の伝送行列をまず求めると 従って影像伝達定数は ということになる。従って通過域と減衰域の境界点が遮断周波数なので、影像伝達定数が純虚数(通過域)から複素数(減衰域)の境界角周波数(ω1,ω2)が遮断角周波数なので という関係式が得られる。 これだけでは未知数(C1.C2.L)に対して方程式がひとつ足らないのでまだ解けない。 わがんねー(ノД`) 著者の解は自分でも確認して魔法的に式の中から虚数単位が消滅するのを確認。 やっぱりf0で影像インピーダンスがRと同値になる条件を使うしかないのかな。 こっから余談。前問の逆回路のように見えるこの問題の回路は、実は前問の回路と同じく帯域通過特性を持っている。顕著な違いと言えば片方の影像インピーダンスがちょうど逆数になっていて、flとfhが前問では零点なのに対してこの問題の回路では極である。反対方向の影像インピーダンスはどちらも同じ様な特性で、flが零点、fhが極と共通している。 それが判ったからといってヒントが得られるわけではないけど、たった3素子の回路でも紙の上で解析すると1ページの計算用紙の裏と表を使っても足らない。それくらい面倒である。それだから大学では古典フィルタ理論を教えなくなってきたのかもしれない。教えてもついていけない学生ばかりだとすればなおさら。人の事は言えないが。 しかし本当に影像インピーダンスを計算しないと解けない問題なのだろうか、そこが問題だ。 しばらく見てなかったドイツの古い理論電気学の教科書に確かいろいろなフィルタ回路の周波数特性の一覧表が書いてあったと思い出し、開いてみたら同じところで3素子フィルタの元ネタが あった( ´∀`) 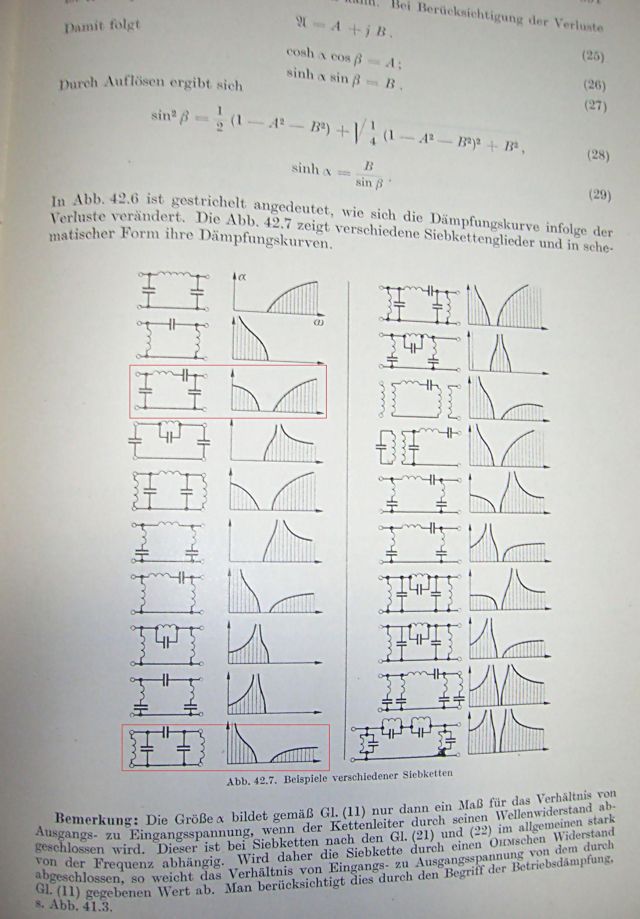 この教科書の巻末の参考文献リストはドイツ人によるドイツ語の書物だけだが、そこに戦後になってからようやく出版された有名なCauerの線型フィルタ理論の書や、線型フィルタを発見しドイツで先駆的な役割を果たしたWagnerの文献も載っている。おそらくそのどちらかから引用したものとおもわれる。つまりWagnerの頃に後のCauerやZobelのように意図的に導出できないにしろLBF,HPF,BPF,BEFがリアクタンス回路で構成できることが判っていたのである。理論的な裏付けはCauerをはじめ後生の人たちによってドイツと北米とで独自に行われていった様子がうかがい知れる。その間に第二次世界大戦があった。 対称π形回路なのですぐに気づかなかったが、一覧表の中に様々な対称形フィルタ回路の減衰特性があり、問題の回路と同じ帯域通過特性を持ち逆L字回路に二等分可能である。 良く考えたら、3素子フィルタ回路は誘導M形フィルタのZ1とZ2を入れ替えたような回路でもある。ということは3素子フィルタというのは実は誘導M形フィルタの帯域通過版なのだろうか。すなわち3素子フィルタは帯域通過形の定Kフィルタをプロトタイプとする誘導M形フィルタではなかろうかという仮説である。それを調べるのは読者の課題としよう( ´∀`) 前は記述が難しいので良く読んでなかったが、以前の問題で発見したような事が視点や表現は異なるものの解説されていた。 そこでアイデアが思いついた、対称回路にしてしまえば、両端で同じ影像インピーダンスになるのだから 2つの半回路を接続し対称π形回路にすればf0で影像インピーダンスZiがRに等しくなるのなら、反対側から見た駆動点インピーダンスもそれと等しくなるはずである。そこからもうひとつの条件式が導かれる。 ずいぶんと見通しが良い方法じゃないか( ´∀`) 厳密的な意味では影像インピーダンスを用いていないとは言えないのだが、アプローチとしては異なるのでよしとしよう。 上の回路図の電源から見た駆動点インピーダンスを求めると ということになる。これをRに関して解くと という驚くべき関係が成り立つことになる。この時点でもうLについて解けたも同然( ´∀`) 先のω1、ω2,の関係式に順次代入して残りの素子定数について解くと ということになる。 やったよママン(ノД`) 諦めずに続けた甲斐があったよ。長い便秘が解消した気分( ´∀`) P.S 著者は影像インピーダンスの条件式から最初にLを導いているが、こちらのアプローチではLについて解くよりも暗算でも出来る程度に楽であったからだ。 |
| フラット表示 | 前のトピック | 次のトピック |
| 題名 | 投稿者 | 日時 |
|---|---|---|
| |
webadm | 2011-7-18 22:55 |
| |
webadm | 2011-7-18 23:12 |
| |
webadm | 2011-7-18 23:53 |
| |
webadm | 2011-7-19 4:48 |
| |
webadm | 2011-7-20 9:12 |
| |
webadm | 2011-7-25 5:11 |
| |
webadm | 2011-7-28 4:35 |
| |
webadm | 2011-7-28 8:42 |
| |
webadm | 2011-7-28 20:30 |
| |
webadm | 2011-7-29 8:25 |
| |
webadm | 2011-7-29 8:37 |
| |
webadm | 2011-7-31 0:28 |
| |
webadm | 2011-8-6 9:22 |
| |
webadm | 2011-8-29 2:14 |
| |
webadm | 2011-8-30 16:35 |
| |
webadm | 2011-8-31 17:17 |
| » |
webadm | 2011-9-4 22:16 |
| |
webadm | 2011-9-10 19:28 |
| |
webadm | 2011-9-12 4:11 |
| |
webadm | 2011-9-17 9:39 |
| |
webadm | 2011-9-17 19:18 |
| |
webadm | 2011-9-18 0:41 |
| |
webadm | 2011-9-18 5:37 |
| |
webadm | 2011-9-18 18:57 |
| |
webadm | 2011-9-18 21:23 |
| |
webadm | 2011-9-18 22:01 |
| |
webadm | 2011-9-20 1:09 |
| |
webadm | 2011-9-20 5:11 |
| |
webadm | 2011-9-20 6:06 |
| |
webadm | 2011-9-20 6:18 |
| 投稿するにはまず登録を | |

