| �ե�å�ɽ�� | ���Υȥԥå� | ���Υȥԥå� |
| ��Ƽ� | ����å� |
|---|---|
| webadm | �������: 2011-9-24 22:12 |
Webmaster   ��Ͽ��: 2004-11-7 �サ��: ���: 3089 |
���������ϩ�β��ϸ��ݲ��� ��˽Ҥ٤��̤ꡢ���Ū�ˤ�Thomson��Heaviside���Ԥä��褦�˳��쥱���֥��Ĺ��Υ���ſ���ϩ�Τ褦�ʺ����Ǹ���ʬ�������ϩ�β������꤬�����������˺ǽ餫�����Ȥ�ˤϿ���Ū���μ��ν��������ʤ�ɬ�פʤΤǡ������˽��äƸ�ˤ���������ʤ������̤Ϥ������ܻؤ��Τ��Ȥ�������١��������ݤĤ����ˤȤɤ�褦��
����Ū�˲��ϸ��ݲ��ϤϤ���ޤǤⰷ�äƤ������������ϩ�ˤĤ��Ƹ��椹�뤳�Ȥˤʤ롣���������ϩ�Ǥ���л���t�������ѿ��˻��İ��ѿ��ؿ��������Ф褤�Τ����Ū�ϡ��ɥ뤬�㤤�� �ۤȤ�ɤ��ŵ���ϩ�ζ��ʽ���ɼԤ�������ʬ�������β�ˡ���μ���ͭ���뤳�Ȥ�����˲���������ʤ�dy/dt�ʤɤε�����о줵���Ƥ����ʤ���ʬ��������Ҳ𤷤Ƥ��롣�������ٸ��ΤäƤ��Ƥ⤳��������롣 ���⤽����ؤ�����ʬ���ܤǤ���dy/dt�ʳ��ˤ�Ʊ����ǰ�ΰۤʤ�ɽ�����о줹��Τ�Ƭ�����𤹤롣���ä����ɤ��ʤäƤ������ȿ��ؤθ�����䤤�����������Ȥ����Ǥ��뤬���ȶ�˵�ʤ��ΤǼ긵�δ��ȡֿ��ػ�ŵ�פ�Ҥ�Ȥ������ʤ��������ˤ���ʬˡ�ˤĤ��Ƥ��������Ƥ��롣 ���ѡ�
�ʤ���ǽ餫�麮�𤷤Ƥ뤸���ʡ��������� ��ʬ�˴ؤ��Ƥϰʲ��Τ褦�˽�Ƥ��� ���ѡ�
�Ȥ��������Ĥ����餷��������ʴ����Dz��Ǥ⤢�������ʤΤ�Ĺ�����ؤ����Ū�ʻ���ˤ�롣��ʬ���������Ǿ����о줷���Τ�Newton�� ������ؤ�����ʬ�Ǥϸ�̩������¸�ߤ�Ƚ��Ȥ������κ����˴ؤ����ʬ���濴�Ǥ��ꡢ���ѤˤϿ���ʤ����ޤ����Τ������ǰ¿����Ʊ��ѽ����櫓�ǤϤ��뤬�� ���Ʋ����ä����ä����� ���������������ϩ�β��ϸ��ݲ��Ϥ͡� ���������ϩ�β��ϸ��ݲ��Ϥϻ��֤��ѿ��Ȥ���ؿ����Ȥ���쳬�⤷���Ϲⳬ����������ʬ�������������˵��夹�롣����ϸ�ŵ���Ϥλ�����͡��ʲ�ˡ�������Ƥ��ơ����������̤���Ѥ��Ʋ��Ȥ�����롣 �����������Ǥ����Ҳ𤹤�Ȥ����ʤ���ʬ���椬���˸���뤳�Ȥˤʤ�Τǡ�ĩ��٤�������������Ƥ���ɬ�פ����롣 ���⤽�⽸�������ϩ�β��ϸ��ݲ��Ϥ���������Τϲ��ʤΡ� ��ʬ�ζ���ʹ���Ƥߤ뤷���ʤ����������ʤ��Ρ� �����������֤����ϩ���֤��Ѳ��������˰������Ű�����ή���ɤΤ褦���Ѳ����뤫�� ���Ƥ������֤�����夯�Τˤɤ�����λ��֤��פ��뤫�� �Ȥ������Ȥˤʤ롣 �ǽ����ϡ��Ÿ�����³����Ƥ��ʤ���ϩ���Ÿ������(t=0)�ǤĤʤ������˲���Ū�˲�ϩ����ή���Ű����ɤΤ褦���Ѳ�����Τ����狼��ʤ��Ȥ�����̣�ˤʤ롣Ʊ�ͤ˴�����³����Ƥ��ƽ�ʬĹ�����֤��вᤷ�������֤�����夤�Ƥ����ϩ�����Ÿ�������������˲���������Τ���狼��ʤ�������Ū��ȯ�������Ű�����ή����������ǻҤ����줿������������ξ����Ρ���ư��˷Ҥ��뤪���줬���롣�Ÿ������줿�곰���Ƥ�¨�¤˼��������֤��Ѳ�����Τ��Τߤ��������ϩ�����ǡ����ͥ륮�����ߤ��륭��ѥ����䥤���������ޤ��ϩ�ǤϤ����ʤ�ʤ����Ȥ��Ť������Τ��Ƥ��롣�ºݤΤȤ������������ϩ�Ǥ��ϩ���Ű�����ή�Ͻֻ������ꤹ�뤬�����Ϥζ��֤��ż��������Ѥ��뤿��줬�ż��ȡ����ȡˤȤʤäƱ����¤��Ƥ��������Ѥ�⤿�餹�������Ȼפ��ʤ�AM�饸����ʹ���Ƥ�����֤Ǽ¸����Ƥߤ���ɤ�����ϩ���Ÿ���Ĥʤ������ȳ��������˥饸������Υ�����ʹ������Ϥ����� �����ܤϡ������ܤβ���Ū�ʤФ��Ĥ����ɤ줯�餤Ĺ��³���Τ��Τꤿ���Ȥ�����Ρ����̤�����Ȥ��Ǥ�������֤Ȥ�������Ȥ������Ƥ����Τ��������롣 �����������䤬���Ϸ�̤ˤ���ä���뤳�Ȥ���Ū�Ȥ��������ĩ�ळ�Ȥˤ���Х���١�������ݤƤ롣 ��������ǽ������椹�뤳�Ȥˤ��褦��������������Ū�ʥ��ץ������ǤϺǽ�˰���Ū����������ʬ�������β���Τä���ǿʤ��ΤǤϤʤ����������Τ�ʤ��Ȥ�������ǻϤ�뤳�Ȥˤ��롣���ʤ��������ޤdzؤ���褿���Ȱʳ��ο������μ���ڤ����ˤ����̤����դ�ʧ���Ȥ������ȤǤ��롣�����Heaviside�λ���˴����Τ��Ƥ����μ������ǹͤ��Ƥߤ褦�Ȥ������ȤǤ��롣�������ǽ�Ū�ˤϺ����Τ��Ƥ�����ʬ�������β�ˡ�Τɤ줫��Ȥ�ɬ�פ����뤬���ǽ餫�餽�줬���뤳�Ȥ�����ȤϤ��ʤ��Ȥ������ȤǤ��롣����ϲ��Ϥ�ĩ�ि��Υ���١�������⤯�ݤĤ����ɬ�פʤ��ȤǤ��롣������Ƥ����ܤϤ���ޤ�˻����Ǥ��ޤäƤ��롣 ����Ū�ˤ�Valkenburg������ˤ����̤�����꤫��ʤ�Ƥ������Ȥ�����ʤ��Ȼפ���L��R��ľ���ϩ�Ǥ��롣�������������Ǥ϶���Ū������ʬ���μ���ե���Ѥ���ΤǤϤʤ������ޤdzؤ���μ������Dz��Ϥ��뤳�Ȥˤ��롣 ��β�ϩ��LRľ���ϩ�ˣ��Ĥ��Ÿ��ʤҤȤĤ�E���⤦�ҤȤĤ������ʭ�E)��ľ�����³���줿��ϩ�����β�ϩ�Ϻ��ޤdzؤ���Ť�碌������ȤäƲ��ϤǤ������Ǥ��롣���ʤ��E��������³�������˲�ϩ��ή��������֤Ǥ���ή��I�Ȥ�����E��ä���������ή���Ѳ��̤��I�Ȥ���ΤǤ��롣 �����ǭ�E���������֭�t�δ֤��Ѳ����������̤��Ȥ��ơ���I�������֤Ǥϭ�E�����㤹��Ȥ��Ƥ����Ū�ˤ�L�αƶ��ǻ��֤ȶ����Ѳ����뤳�Ȥ�ͽ�ۤ���롣L��ξü���Ű��߲���ή�����ή���Ѳ�®�٤����㤹�뤳�ȤǤ˾崬�dzؤ�Ǥ���Τǡ��ֻ�Ū�ˤϰʲ��δط�������Ω�Ĥ��Ȥˤʤ롣 �ޤ� �Ǥ���ΤǤ������������� �Ȥ������Ȥˤʤ롣������I/��t�˴ؤ������������ ���줫����ήI�λ��֤˴ؤ���ؿ������ˤϤɤ�������ʡ��������� �����ʤ����ƤϤޤä��� Valkenburg���ܤ�ȡ������ˤϡ��ޤ� �֤��� �Ȥ��Ƥ���ξ�դ�e^Pt��褸��� ������Ie^Pt����ʬ��ͤ���� �Ȥ������Ȥˤʤ롣����ϸ�����ʬ�������α��դ�Ʊ�ͤʤΤ� �Ȥ������Ȥˤʤ롣����ʤ�ξ�դ���֤���ʬ����Ф褯 �Ȳ롣���줬��ξ���ʬ�������ΰ��̲�Ǥ��롣 ������t����Ȥ���� �Ȥ������Ȥˤʤ뤳�Ȥ��顢���̲�����ब����ǡ�����ब���֤ȤȤ�˾ü�������ϲ�ȸƤФ���ΤǤ��뤳�Ȥ��狼�롣 �ʤ����ñ����ʤ����ʡ��ϡ����� �Ȥ�����K����ʬ��������������ͤϤɤ���äƷ�ޤ�Τ������� �����Ÿ������äƤ��ʤ����֤���ִ�Ū�˲ä������ˤ�t=0��I=0�ʤ櫓�����顢K=-E/R�Ȥ������Ȥˤʤ롣 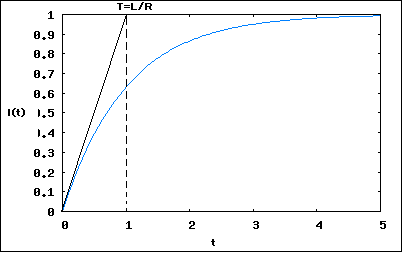 ���٤ϴ����Ÿ�E�����äƤ������(I=E/R)�����Ű���E1�˽ִ�Ū���Ѥ������Ϥɤ���������������(t��0)����ή��E1/R�Ȥʤ�Ϥ��Ǥ��뤫�顢K=E/R-E1/R�Ȥ������Ȥˤʤ롣 ��μ���ꡢE1=0�Ȥʤä������Ÿ��������줿���� �Ȥ������Ȥˤʤ롣  ���ϲ�λؿ����ϻ����T=L/R���������� ��ɽ����롣�����T�Σ��ܤλ��֤��в᤹��Ȥۤ������֤Ȥߤʤ��뤳�Ȥ�t=0��t=5T�λ���e^{t/T}�����������餫�� �ɤ��ܤˤ�Ƥʤ������֤Ǥ��Ÿ�E����ήI���ߤ����Ѳ�ʬ�έ�E��ͤ�����ͳ�ϡ��ɤ��ܤˤ����������˽�Ƥ�����ʬ��������Ω�������´��Τ����Τ��ä�����Ǥ��롣�ǽ�ɤ��˰��´������뤫�狼��ʤ��ä���������ή�Dz��Ϥ��ƤߤƤ�����ͳ���狼�ä��� Newton��Leibniz�λ������ʬˡ���Ѳ��̤�ͭ���ͤ�Ȥꤽ����ʬ��Ϣ³�Ƕ����Ǥ��٤���ʬ��ǽ�Ǥ��뤳�Ȥ�����Ȥ��Ƥ��롣���θ�θ�ŵ���ϤǤ⤳��������Ѥ�äƤ��ʤ���������Ф���Heaviside��ĩ����ſ���ϩ�Ǥ�ľή��ON/OFF�Ȥ�����Ϣ³���������������ʬ������Ǥ������Ǥ���ʬ�Բ�ǽ�ʴؿ���ɬ�פ����ä��������Ǥ�ʤ�ï�⤳�Τ��ȤˤĤ��ƤϿ��줺�˸�ŵ���Ϥ����̤�ή�Ѥ��Ƥ������������Ȱ��´����Ƥ����Τ��ä��� Heaviside���ȼ��ˤ�������˼���Ȥ�������κݤ˳��ʴؿ��ȸƤФ�볬�ʾ��˼�ꤦ���ͤ���������Ķ�ؿ���Ƴ������ɬ�פ����ä��� Heaviside��Ʊ����α��ѿ��ؼ�Bromwich��Heaviside�ȿ�̩�˼�������Ϥ����ʤ��顢Heaviside�α黻��ˡ��Ĵ�²����ǤȤ�������Laplace�Ѵ��Ȥ����Τ���ʣ����ʬ(Bromwich��ʬ�ˤ�¸�ߤ�õ�����Ƥ���Bromwich�Τ�����ʸ�ϴ��˴������Ƥ�������Heaviside�λ��˽��Ǥ����ޤ�ȯɽ����ʤ��ä��ʸ��ߤ⤽����"An introduction to the theory of infinite series."�����Τ���Ƥ���ˡ����κݤ�Heaviside�������˽Ĥ���"Campbridge�ο��ؼԤǤ����ʱ黻��ˡ�Ρ�������������Ǥ��ʤ��Ǥ�����..."�Ȥ������դ�����礤�ˤ��Ƥ�ä������ʸ��ܤ��Ƥ��롣Ʊν�ο��ؼԤ���Heaviside�Ȥζ�Ʊ�����̤Ǥ���ˤ�ؤ�餺���ˤ����Ф����Τ褦�ʤ��Ȥ�ΤϿ�ƻ��ȿ������������������Ӥ�������������Ū���ɤ����ޤ줿Bromwich�ϲ�²�ȻҶ���Ĥ��Ƽ������������������� �ä��ˤ�ɤ����� �ŵ���ϩ���Ÿ���ON/OFF�Τ褦����Ϣ³���Ϥ˴ؤ����ư����Ϥ��뤿��˸�ŵ���Ϥμ�ˡ���٤��٤��Ȥ��Τϴ��ʤä������Ȥ������Ȥ���ͳ��ޤ�Ƥ���Ǥ狼�ä��Ȼפ���t=0�����Ȥ�Ϣ³����ͤ��뤿��ˤ��Ÿ���ON/OFF�Τ褦����Ϣ³�ؿ���Ϣ³�ؿ���̵�¤νŤ�碌��ɽ����Ф褤�櫓�Ǥ��롣��������Ф��줾���Ϣ³�ؿ�����Ÿ����б������ƽŤ�碌�����Dz��ϲ�ǽ�Ǥ��롣������̵�¤ο��νŤ�碌�ҤȤĤҤȤĤˤĤ��Ʋ��Ϥ���ΤǤ�̵�¤λ��֤������롣�ʤΤǸ�ŵ���Ϥ�Ȥ��Τ�����ۤ����褤�Ȥ���������ã���롣����������Ϥ�ͭ�¿���Ϣ³�ؿ��Ǥ���Ф���ɬ�פϤʤ����⤷��ʤ��� ���Ǥ˾崬��Fourier�����Fourier�Ѵ���ؤ��������Ĵ�²��Ϥμ�ˡ���ΤäƤ���櫓�ǡ�����Ǥ���и�ŵ���Ϥ�����Ф����Ȥʤ��ǽ餫��Ĵ�²��Ϥ�Ȥ��Ф褤�ΤǤ��롣�ºݼ긵���ŵ��ز���ǤΡֲ��ϲ�ϩ���ϡפǤϸ�ŵ���ϤϽ��Ϥ����ǡ�����Ϥ���黻��ˡ�ʼºݤˤ�Laplace�Ѵ��ˤ����⤵��ʹߤϤ���Τߤ��Ѥ��Ƥ��롣 �ǽ�˰��´����븶���Ǥ������t=0������Ǥδط��ؿ�����Ϣ³���Ǥ��롣���Τ����ŵ���Ϥμ�ˡ��Ȥ����ˤϡ�t>0�ˤĤ��ƤΤ߹ͤ���ɬ�פ����롣����������ϰ��´������롣ľ��Ū�ˤϻ��ּ����t=0�Ǥ��Ѳ���̵�뤷�Ƥ���ľ��ξ��֤���������Ω�Ƥʤ���йԤ��ʤ�����ï���������Ƥ��ʤ������ؤȸ��äƤ��ޤ��Ф���ޤǤ������⤦�����ޤȤ�ʸ��̤��Τ褤�ͤ����Τ��ʤ��Τ��� ���礦�ɳ��äפ����ؤˤ��ơַ������Ϻ��䤬Ω�äƤ�����֤�����˹Ԥ��ʤ��褦�ˡ������ƺ����Ƥ�������������ͤ���褦�ˡ����ä���ȿ��¦���֤ä���夺���ꤷ�ƤϤ����ʤ��פȶ����Ƥ����ʤ�ޤ����⡢������鷺�˳��äפ��ն��Ĵ�٤�褦�ˤȸ������ï�������鳳���������˷�ޤäƤ���ʡ��ϡ����� (2011/9/25) youTube��MIT��differential Equation�ιֵ��ļ��֤��Ƥ褦�䤯RCľ���ϩ���ä�������äȽФƤ����Ȥ��ˤϤ����������������ޤ�����Τˣ����֤�ιֵ���ɬ�פʤΤ��Ȥ����Τ˶ä����긵�Τɤο��ؤ��ܤˤ�Ƥʤ�����Ū�������μ����֤������Ƥ�����٤ǡ���������������ʤ��Ȥ���ʬ��������ʬ�θ����Τ������Ĥ��ΤäƤ��뤳�Ȥ�����Ȥ������Ȥ��ǧ����ؤ�ʪ���إ������Ȥ��Ǥϡ���ʬ����ʬ�θ������֤��ɥ��Ǵ�����Ƭ�ȼ�˲�����������ˡ��ȤäƤ���Ȥ����⤢��餷������������ʪ���ؼ�Landau�⥻�ߥʡ����ô�˾�γ����ˤϤޤ���ʬ�������Ϳ���ơ�����Τ������������Ƥ����� ����ʤΤ˺���������ʬ�ν�ʪ�����ƤϤ�������롣 ����������������RCľ���ϩ�ˤĤ��Ƥ��ä�����ɤ�������Dz��Ϥ��Ƥߤ褦 RLľ���ϩ�λ��Ȱ�äơ��Ÿ���E(t)�Ȼ��֤δؿ��ˤ��������Τۤ���Ǥ�դν������Ϳ�����롣���Ȥϲ�ϩ��ή�����ή��Ф����櫓���� C��ξü���Ű���C���ߤ���줿�Ų�(��ή�λ�����ʬ�ˤ���������C�dz�ä��ͤ��Ű��ʤΤǡ����줬�ФƤ��롣��R��ξü���Ű��߲���ή�����ήI(t)�����㤹�롣C��R��ξü���Ű��߲��ι�פ��Ÿ�e(t)�Ⱦ�˶ѹդ��Ƥ���Ȥ����������Ƥ��롣 ��ʬ�ब�ޤޤ�Ƥ���Τ���ʬ�������ˤʤäƤ��뤬������ϻ��֤�ξ�դ���ʬ���뤳�Ȥˤ�äư쳬����ʬ�������ˤʤ� �����RLľ���ϩ�λ���Ʊ�ͤ�ɸ�������������� �Ȥ������Ȥˤʤ롣 ������Ʊ�ͤ�integral factor(e^{Pt})��ξ�դ˾褸����������� �Ȥ������Ȥˤʤ롣���Ȥ�ξ�դ���֤���ʬ����Ф褯 �Ȥ������Ȥˤʤ롣 ��ʬ��ʬ�ब�ä��ʤ��ΤǤ������ɤ������餤���Ǥ����ʡ��������� ������� �Ȥ����t��0�ϴ��������֤�I=0�Ǥ���Ȥ���С�������ʬ���ϰϤ�0+(0�����+���ζ�˵�ˤ���t���ϰϤ����Ǥ褤�Τ� �Ȥ������Ȥˤʤ롣 ��ʬ���K���Ĥ�ΤǤ����ɤ�����Ф褤�Ǥ����ʡ��������� t��0�Ǥ������֤Ǥ���Ȥ����Τǡ��Ÿ��Ű���E1���Ѥ�ä��ݤν����ήI0�� �Ȥ������Ȥˤʤ롣���ä�t=0+��I=I0�Ȥ������ʬ���K�� �Ȥ������Ȥˤʤ롣 ���äƤ���β����������� �Ȥ������Ȥˤʤ롣 �㤨��E0=0��E1=1��C=R=1�Ȥ�������I��ץ��åȤ���� 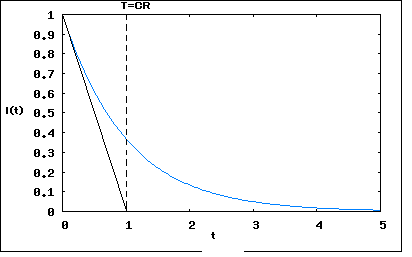 �Ȥ������Ȥˤʤ롣 �դ�E0=1��E1=0�Ȥ������ˤ� 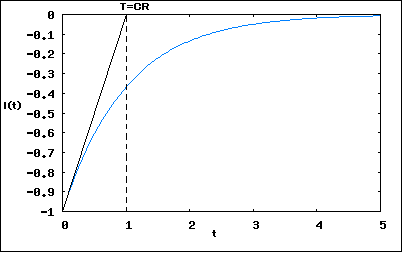 �Ȥ������Ȥ�Ƴ�Ф����ʤ����ݤǥȥ�å��������Ű���ä����ݤȼ��ʧ�ä��ݤΤɤ���β��ޤ�Ǥ������ǤϤɤ��ܤˤ��Ƥ��ʤ������Ǥ��롣 �Ű�E�������ϡ���ήI��®�٤��ɤ��ؤ���ȡ�RLľ���ϩ�ξ����Ƥ֡�RCľ���ϩ�ϥХͤߤ����ʤ�ΤǤ��뤳�Ȥ��狼�롣 ������äƤߤƤ狼��Τϡ����������쳬�ξ���ʬ��ʬ�������Ǥ��äƤ�ΤˤϽ�ʬ�����դ�ʧ��ɬ�פ��Ȥ������Ȥȡ�ʣ���Υ������ҤȤĤβ��ɽ�����ȤϺ���ȼ���Ȥ������ȤǤ��롣����Ū�˰��̲�¸�ߤ����Ȥ��Ƥ⡢��Ū�ν�������������ü���ǽ�Ū������ɬ�פ����롣 �¤Ϥ��Τ褦�ʽ���Ū����ʬ�������β�Ǥϡ�Heaviside��ĩ����褦���ſ���ϩ�β��ϤˤϤϤʤϤ��Խ�ʬ�Ǥ��롣�Ȥ����Τ��������ſ��ϸ��ɸ��Ȥʤä��⡼�륹���Τ褦����ή��ñ�����³�ǤϤʤ���¿�������Ǥ��ä�����������礦�ɸ����Gigabit Ethernet�Τ褦�ˤҤȤĤ�����ϩ��Ϳ�����Ű���٥��ʣ���ʳ��ߤ��ơ����줾��˰ۤʤ뿮����ͤ�⤿���Ƥ����ΤǤ��롣����¦�Ǥϸ�ή�פοˤο�����Ƥɤ��ͤ������Ƥ��Ƥ��뤫�ſ����դ��и�Ū��Ƚ�̤��Ƥ����ΤǤ��롣���줬Heaviside���ȼ��γ��ʴؿ���Ƴ������ɬ�פ����ä���ͳ�Ǥ⤢�롣�ä�������ϩ�Ͻ��������ϩ�ǤϤʤ�ʬ�������ϩ�Ǥ��롣ʬ�������ϩ�β��ϸ��ݲ��Ϥϲ����κǽ��Ϥdzؤ֤��Ȥˤʤ�Ǥ����ʥơ��ޤǤ��롣 ��δ�ñ��RLľ���ϩ��RCľ���ϩ����Ǥ��Ű����Ѳ�ľ���������֤Ȥ��Ƥ������������֤Ǥʤ������Ѳ����������ˤϤ��β�Ȥϰۤʤ��ΤȤʤ롣�ſ�����γ��쥱���֥��Ȥä��̿��Ǥϰ���δֳ֤��֤��ƿ�����Ѳ�������ɬ�פ����ä�����������ο����Ѳ��ˤ����ϸ��ݤ���ʬ���ꤹ�����˼����ο��������Ȳ��ϱ��������蘆�äƼ���¦��Ƚ�̤������������꤬������ˤ���Ǥ��롣���Τ��᳤�쥱���֥��Ĥ��ä��ſ���ʸ�����äƤ���������Τ�¿��ʻ��֤��פ������ɤ���Τˤ�¿��ʻ��֤��פ����Τ��ºݤǤ��롣����Ǥ����Ǽ����Ϥ���Τ����������ä��� ����Ū���Ű��Υ��ƥå��Ѳ������Ǥ��Ѳ������ΰ����ˤĤ��Ƥ��ܤˤ�äƤޤ��ޤ��Ǥ��롣�����ο��ؤǤϴؿ�����Ϣ³����ͭ�¤Ǥ������ʬ��ǽ�Ȥ���Ƥ���Τϡ���Ϣ³���������Ϣ³���ϰϤ���ʬ�����¤��뤳�Ȥ�Cauchy�μ��ͤ�������Ȥ��뤫��Ǥ��롣�����Riemann��ʬ�Ǥ�����Ѥ���Ƥ��롣�������Ѳ������������ʬ����Ȥ������Ȥ��ۤȤ�ɤ��ŵ���ϩ�β��ϲ��Ϥ������ǤϻȤ��Ƥ��롣���������Τ��˹ֵ����֤⾯�ʤ��Ƥ��ष�����ּԤ���ô�⾯�ʤ��ƺѤ�Ȥ������åȤ�⤿�餷����������������ܼ����Ƥ��ޤ��Ȥ���»����⤿�餷�Ƥ��롣 �ɤ��ܤˤ�Ƥ�����ϸ��ݲ��Ϥ���ˡ�Ͼ���ʬ�������β�ˡ���ŵ���ϩ�˱��Ѥ�����ΤǤ��롣���Τ�����Ͽ��ڡ����β�����ɤ������Ǥ����ΤǤϤʤ����������λ��Υɥ��Τ褦�˰פ�����Τ����ʡ�������Τر齬���Ѥ߽ŤͤƤ��ä��ΤdzФ��뤷���ʤ������ϤDz�����ʤ���������ϤDz��Ȥ�ҤȤĤ���ɸ���֤��Τ�����ǡ�����ˤ�ä�Ĺ������١��������ݤĤ��Ȥ�����롣��ͤζ�ϫ�����θ��Ǥ⤢�롣��ˤ���ɴǯ�����Ƥ��ɤäƤ���ƻ���ԥ��ԡ��ɤ����θ����뤳�Ȥˤʤ�Τ�����и礬ɬ�פǤ��롣 �����Ǥɤ����Ƥ����ʬ�������β�ˡ�ˤĤ����η�Ū���μ���������뤳�Ȥ����ʤ�������������ǤϤ��뤬�����̵�����Ʋ��ϸ��ݲ��Ϥ��������Ȥ����Τϡ����ϸ��ݲ��Ϥ��˷�̤����Τꤿ�����ߤ��Ƥ���Τ�Ʊ���Ǥ��롣��ϩ���ߥ�졼�������Ϥ�����������������Ƥ���뤿��ʣ�����ŻҲ�ϩ�ǤϤ������뤳�Ȥ�¿��������̤��ɤ���������������뤫Ƚ�Ǥ���ˤϤ�Ϥ�����ˤ����Ϥ��Բķ�Ǥ������� P.S ���ɤ��ɤ������ϤˤʤäƤ��ޤä�������ɤϾ���ʬ����������Ȥˤʤ롣����Ū�ʲ�ˡ���Ȥ���äȴ��ʤä������Τǡ���äȴ��ؤǴְ㤤�ξ��ʤ���ˡ��Ȥ��Τ�˾�ޤ������������� ���̤�Ǻ�ߤ˲��Ū����ˡ�������Τ�Heaviside�Ǥ��ä����쳬����ʬ���������٤Ǥ���п��ؤΤ����餤�ΤĤ��Ƕ��ʽ�Ū�˲����Ƥ�褤���⤷��ʤ����ⳬ����ʬ�������ˤʤä������Ȥ������Ȥ��Τ��ɤ��������� |
| �ե�å�ɽ�� | ���Υȥԥå� | ���Υȥԥå� |
| ��̾ | ��Ƽ� | ���� |
|---|---|---|
| |
webadm | 2011-9-22 13:23 |
| » |
webadm | 2011-9-24 22:12 |
| |
webadm | 2011-10-10 3:34 |
| |
webadm | 2011-10-10 10:09 |
| ��Ƥ���ˤϤޤ���Ͽ�� | |

