Gan's blog - フォーラム

« 1 2 (3) 4 5 6 7 »

投稿者	スレッド
webadm	投稿日時: 2010-5-30 12:37
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3090	二端子対回路の並列接続次ぎの問題は二端子対回路を並列接続した場合の問題点について。これは理論の時に既にやってしまったので割愛。共通帰線を持たない二端子対回路を並列接続する場合には、端子対に理想変成器を挿入すれば解決できるというもの。

webadm	投稿日時: 2010-5-30 12:45
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3090	もうひとつの：４端子定数次ぎは再び４端子定数の問題。既知の４端子定数を持つ２つの異なる二端子対回路を並列接続した場合の４端子定数をもとめよというもの。図で表すと４端子定数の縦列接続は計算し易いが、並列接続はそうではない。著者はYパラメータに変換して並列接続の計算を行い、それを４端子定数に変換しているが、別の方法でやってみよう。以下の様に各端子対の電圧と電流を定義するそれぞれの端子対の電圧と電流を座標とするベクトルを考えると、以下の関係が成り立つここから解法の見通しを立てることになる。 Fは回路全体の４端子定数で構成される伝送行列でベクトルPをベクトルQに線形変換する。 F',F''は個々の回路の４端子定数で構成される伝送行列でそれぞれP'をQ'へ、P''をQ''へ線形変換する。 $\begin{eqnarray}<br />Q&=&F P=\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]P\\<br />Q^{\'}&=&F^{\'} P^{\'}=\left[\begin{array}<br />A_1 & B_1\\<br />C_1 & D_1<br />\end{array}\right]P^{\'}\\<br />Q^{\'\'}&=&F^{\'\'} P^{\'\'}=\left[\begin{array}<br />A_2 & B_2\\<br />C_2 & D_2<br />\end{array}\right]P^{\'\'}<br />\end{eqnarray}$ 以下に示す通りにPはP'とP''、QはQ'とQ''の以下のような線形結合で表される。 $\begin{eqnarray}<br />P&=&\left[\begin{array}<br />E_2\\<br />I_2<br />\end{array}\right]=\left[\begin{array}<br />\frac{1}{2} & 0\\<br />0 & 1<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />I^{\'}_2<br />\end{array}\right]+\left[\begin{array}<br />\frac{1}{2} & 0\\<br />0 & 1<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />I^{\'\'}_2<br />\end{array}\right]=\left[\begin{array}<br />\frac{1}{2} & 0\\<br />0 & 1<br />\end{array}\right]P^{\'}+\left[\begin{array}<br />\frac{1}{2} & 0\\<br />0 & 1<br />\end{array}\right]P^{\'\'}=\left[\begin{array}<br />\frac{1}{2} & 0\\<br />0 & 1<br />\end{array}\right]\left(P^{\'}+P^{\'\'}\right)\\<br />Q&=&\left[\begin{array}<br />E_1\\<br />I_1<br />\end{array}\right]=\left[\begin{array}<br />\frac{1}{2} & 0\\<br />0 & 1<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />I^{\'}_1<br />\end{array}\right]+\left[\begin{array}<br />\frac{1}{2} & 0\\<br />0 & 1<br />\end{array}\right]\left[\begin{array}<br />E_1\\<br />I^{\'\'}_1<br />\end{array}\right]=\left[\begin{array}<br />\frac{1}{2} & 0\\<br />0 & 1<br />\end{array}\right]Q^{\'}+\left[\begin{array}<br />\frac{1}{2} & 0\\<br />0 & 1<br />\end{array}\right]Q^{\'\'}=\left[\begin{array}<br />\frac{1}{2} & 0\\<br />0 & 1<br />\end{array}\right]\left(Q^{\'}+Q^{\'\'}\right)<br />\end{eqnarray}$ だめだ熱が出てきた(;´Д`) いきなり演繹的に考えても見通しがつかない。ここはGauss大先生に習って帰納法でやってみよう。まず簡単な回路を並列接続して４端子定数がどうなるか見てみよう。最初に以下の回路を考えよう２つの小回路の４端子定数は以前の問題の解答で既出であるし、並列にした場合、Z1とZ2が並列になるだけなので $\begin{eqnarray}<br />F^{\'}&=&\left[\begin{array}<br />A_1 & B_1\\<br />C_1 & D_1<br />\end{array}\right]=\left[\begin{array}<br />1 & Z_1\\<br />0 & 1<br />\end{array}\right]\\<br />F^{\'\'}&=&\left[\begin{array}<br />A_2 & B_2\\<br />C_2 & D_2<br />\end{array}\right]=\left[\begin{array}<br />1 & Z_2\\<br />0 & 1<br />\end{array}\right]\\<br />F&=&\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]=\left[\begin{array}<br />1 & \frac{Z_1 Z_2}{Z_1+Z_2}\\<br />0 & 1<br />\end{array}\right]<br />\end{eqnarray}$ 従って伝達インピーダンス(B)は２つの小回路の伝達インピーダンス(B1,B2)を並列にしたものになることがわかる。次ぎに以下の回路を見てみようこれも以前の問題の解答で既出なので $\begin{eqnarray}<br />F^{\'}&=&\left[\begin{array}<br />A_1 & B_1\\<br />C_1 & D_1<br />\end{array}\right]=\left[\begin{array}<br />1 & 0\\<br />\frac{1}{Z_1} & 1<br />\end{array}\right]\\<br />F^{\'\'}&=&\left[\begin{array}<br />A_2 & B_2\\<br />C_2 & D_2<br />\end{array}\right]=\left[\begin{array}<br />1 & 0\\<br />\frac{1}{Z_2} & 1<br />\end{array}\right]\\<br />F&=&\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]=\left[\begin{array}<br />1 & 0\\<br />\frac{Z_1+Z_2}{Z_1 Z_2} & 1<br />\end{array}\right]=\left[\begin{array}<br />1 & 0\\<br />\frac{1}{Z_1}+\frac{1}{Z_2} & 1<br />\end{array}\right]<br />\end{eqnarray}$ 従って伝達アドミッタンス(C)はそれぞれの伝達アドミッタンス(C1,C2)の並列したものと変わらないということがわかる。この事実から伝達インピーダンスと伝達アドミッタンスについての一般化した場合の以下の予想を立てることができる。 $\begin{eqnarray}<br />B&=&\frac{B_1 B_2}{B_1+B_2}\\<br />C&=&C_1+C_2<br />\end{eqnarray}$ 数学的にはこれは証明を待つ命題ということになる。証明さえできれば即時に定理となる。証明を考える前に、もう少し複雑なケースを考えてみよう。これはπ形回路の各素子がそれぞれ並列接続されるのでπ形回路の４端子定数が解れば結果は自明である。 π形回路のアドミッタンス行列は以前の問題の解答で以下の通り導出済み $\begin{eqnarray}<br />\left[\begin{array}<br />Y_{11} & Y_{12}\\<br />Y_{21} & Y_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />\frac{1}{Z_2}+\frac{1}{Z_1} & -\frac{1}{Z_2}\\<br />-\frac{1}{Z_2} & \frac{1}{Z_2}+\frac{1}{Z_3}<br />\end{array}\right]<br />\end{eqnarray}$ またアドミッタンス行列の４端子定数への変換も以前の問題で以下の通り導出している $\begin{eqnarray}<br />\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]&=&\left[\begin{array}<br />-\frac{Y_{22}}{Y_{21}} & -\frac{1}{Y_{21}}\\<br />-\frac{Y_{11}Y_{22}-Y_{12}Y_{21}}{Y_{21}} & -\frac{Y_{11}}{Y_{21}}<br />\end{array}\right]<br />\end{eqnarray}$ 従ってπ形回路の４端子定数は $\begin{eqnarray}<br />\left[\begin{array}<br />Y_{11} & Y_{12}\\<br />Y_{21} & Y_{22}<br />\end{array}\right]&=&\left[\begin{array}<br />\frac{1}{Z_2}+\frac{1}{Z_1} & -\frac{1}{Z_2}\\<br />-\frac{1}{Z_2} & \frac{1}{Z_2}+\frac{1}{Z_3}<br />\end{array}\right]\\<br />\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]&=&\left[\begin{array}<br />-\frac{Y_{22}}{Y_{21}} & -\frac{1}{Y_{21}}\\<br />-\frac{Y_{11}Y_{22}-Y_{12}Y_{21}}{Y_{21}} & -\frac{Y_{11}}{Y_{21}}<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />\frac{\frac{1}{Z_2}+\frac{1}{Z_3}}{\frac{1}{Z_2}} & \frac{1}{\frac{1}{Z_2}}\\<br />\frac{\left(\frac{1}{Z_2}+\frac{1}{Z_1}\right)\left(\frac{1}{Z_2}+\frac{1}{Z_3}\right)-\frac{1}{Z_2}\frac{1}{Z_2}}{\frac{1}{Z_2}} & \frac{\frac{1}{Z_2}+\frac{1}{Z_1}}{\frac{1}{Z_2}}<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />1+\frac{Z_2}{Z_3} & Z_2\\<br />\frac{Z_1+Z_2+Z_3}{Z_1 Z_3} & 1+\frac{Z_2}{Z_1}<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。途中で以前の問題で導いた式に転記ミスがあって嵌った。訂正しやり直した。この結果からπ形回路の並列接続時の４端子定数は、各素子が並列接続されたπ形回路になることから $\begin{eqnarray}<br />\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]&=&\left[\begin{array}<br />1+\frac{Z_2}{Z_3} & Z_2\\<br />\frac{Z_1+Z_2+Z_3}{Z_1 Z_3} & 1+\frac{Z_2}{Z_1}<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />1+\frac{\frac{Z^{\'}_2 Z^{\'\'}_2}{Z^{\'}_2+Z^{\'\'}_2}}{\frac{Z^{\'}_3 Z^{\'\'}_3}{Z^{\'}_3+Z^{\'\'}_3}} & \frac{Z^{\'}_2 Z^{\'\'}_2}{Z^{\'}_2+Z^{\'\'}_2}\\<br />\frac{\frac{Z^{\'}_1 Z^{\'\'}_1}{Z^{\'}_1+Z^{\'\'}_1}+\frac{Z^{\'}_2 Z^{\'\'}_2}{Z^{\'}_2+Z^{\'\'}_2}+\frac{Z^{\'}_3 Z^{\'\'}_3}{Z^{\'}_3+Z^{\'\'}_3}}{\frac{Z^{\'}_1 Z^{\'\'}_1}{Z^{\'}_1+Z^{\'\'}_1} \frac{Z^{\'}_3 Z^{\'\'}_3}{Z^{\'}_3+Z^{\'\'}_3}} & 1+\frac{\frac{Z^{\'}_2 Z^{\'\'}_2}{Z^{\'}_2+Z^{\'\'}_2}}{\frac{Z^{\'}_1 Z^{\'\'}_1}{Z^{\'}_1+Z^{\'\'}_1}}<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />1+\frac{\frac{Z^{\'}_2 Z^{\'\'}_2}{Z^{\'}_2+Z^{\'\'}_2}}{\frac{Z^{\'}_3 Z^{\'\'}_3}{Z^{\'}_3+Z^{\'\'}_3}} & \frac{Z^{\'}_2 Z^{\'\'}_2}{Z^{\'}_2+Z^{\'\'}_2}\\<br />\frac{Z^{\'}_1 Z^{\'\'}_1\left(Z^{\'}_3+Z^{\'\'}_3\right)+Z^{\'}_3 Z^{\'\'}_3\left(Z^{\'}_1+Z^{\'\'}_1\right)+\frac{Z^{\'}_2 Z^{\'\'}_2\left(Z^{\'}_1+Z^{\'\'}_1\right)\left(Z^{\'}_3+Z^{\'\'}_3\right)}{Z^{\'}_2+Z^{\'\'}_2}}{Z^{\'}_1 Z^{\'\'}_1 Z^{\'}_3 Z^{\'\'}_3} & 1+\frac{\frac{Z^{\'}_2 Z^{\'\'}_2}{Z^{\'}_2+Z^{\'\'}_2}}{\frac{Z^{\'}_1 Z^{\'\'}_1}{Z^{\'}_1+Z^{\'\'}_1}}<br />\end{array}\right]<br />\end{eqnarray}$ という複雑怪奇な結果になる。このことから先に立てた予想は以下の様に修正されなければならない。 $\begin{eqnarray}<br />B&=&\frac{B_1 B_2}{B_1+B_2}\\<br />\end{eqnarray}$ さてここからどうすんだ。A,C,Dについては謎のままである。T形回路の並列接続時は各素子の並列接続とはならないので簡単に回路全体の４端子定数を見いだすことは容易ではなく、もはや一般的な解法を必要とする。もうひとつL形回路の並列接続を考えておこう。それぞれの小回路の４端子定数は４端子定数が既出の回路の縦続接続として導くことができるので $\begin{eqnarray}<br />\left[\begin{array}<br />A_1 & B_1\\<br />C_1 & D_1<br />\end{array}\right]&=&\left[\begin{array}<br />1 & 0\\<br />\frac{1}{Z^{\'}_1} & 1<br />\end{array}\right]\left[\begin{array}<br />1 & Z^{\'}_2\\<br />0 & 1<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />1 & Z^{\'}_2\\<br />\frac{1}{Z^{\'}_1} & 1+\frac{Z^{\'}_2}{Z^{\'}_1}<br />\end{array}\right]\\<br />\left[\begin{array}<br />A_2 & B_2\\<br />C_2 & D_2<br />\end{array}\right]&=&\left[\begin{array}<br />1 & Z^{\'\'}_2\\<br />0 & 1<br />\end{array}\right]\left[\begin{array}<br />1 & 0\\<br />\frac{1}{Z^{\'\'}_3} & 1<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />1+\frac{Z^{\'\'}_2}{Z^{\'\'}_3} & Z^{\'\'}_2\\<br />\frac{1}{Z^{\'\'}_3} & 1<br />\end{array}\right]<br />\end{eqnarray}$ ということになる。全体の回路はZ2がZ2'とZ2''の並列接続になったπ形回路であるので $\begin{eqnarray}<br />\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]&=&\left[\begin{array}<br />1+\frac{Z_2}{Z_3} & Z_2\\<br />\frac{Z_1+Z_2+Z_3}{Z_1 Z_3} & 1+\frac{Z_2}{Z_1}<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />1+\frac{\frac{Z^{\'}_2 Z^{\'\'}_2}{Z^{\'}_2 +Z^{\'\'}_2}}{Z^{\'\'}_3} & \frac{Z^{\'}_2 Z^{\'\'}_2}{Z^{\'}_2 +Z^{\'\'}_2}\\<br />\frac{Z^{\'}_1+\frac{Z^{\'}_2 Z^{\'\'}_2}{Z^{\'}_2 +Z^{\'\'}_2}+Z^{\'\'}_3}{Z^{\'}_1 Z^{\'\'}_3} & 1+\frac{\frac{Z^{\'}_2 Z^{\'\'}_2}{Z^{\'}_2 +Z^{\'\'}_2}}{Z^{\'}_1}<br />\end{array}\right]<br />\end{eqnarray}$ 上記の結果から注目すべきは、 $\begin{eqnarray}<br />C&=&\frac{Z^{\'}_1+\frac{Z^{\'}_2 Z^{\'\'}_2}{Z^{\'}_2 +Z^{\'\'}_2}+Z^{\'\'}_3}{Z^{\'}_1 Z^{\'\'}_3}\\<br />&=&\frac{1}{Z^{\'}_1}+\frac{1}{Z^{\'\'}_3}+\frac{\frac{Z^{\'}_2 Z^{\'\'}_2}{Z^{\'}_1 Z^{\'\'}_3}}{Z^{\'}_2 +Z^{\'\'}_2}\\<br />&=&C_1+C_2+\frac{\left(A_2-A_1\right)\left(D_1-D_2\right)}{B_1+B_2}<br />\end{eqnarray}$ ということである。従ってここまでの結果から以下の予想が得られる $\begin{eqnarray}<br />B&=&\frac{B_1 B_2}{B_1+B_2}\\<br />C&=&C_1+C_2+\frac{\left(A_2-A_1\right)\left(D_1-D_2\right)}{B_1+B_2}<br />\end{eqnarray}$ あとA,Dが残っている。ここで気残りなのが一端C=C1+C2という予想をたてたものの、π形回路の並列問題でそれが否定されたわけだが、修正されたCの関係式はπ形回路の並列接続でも成り立つのだろうかという点である。 π形回路の並列接続時は重複するが再掲するとこうだった $\begin{eqnarray}<br />\left[\begin{array}<br />A_1 & B_1\\<br />C_1 & D_1<br />\end{array}\right]&=&\left[\begin{array}<br />1+\frac{Z^{\'}_2}{Z^{\'}_3} & Z^{\'}_2\\<br />\frac{Z^{\'}_1+Z^{\'}_2+Z^{\'}_3}{Z^{\'}_1 Z^{\'}_3} & 1+\frac{Z^{\'}_2}{Z^{\'}_1}<br />\end{array}\right]\\<br />\left[\begin{array}<br />A_2 & B_2\\<br />C_2 & D_2<br />\end{array}\right]&=&\left[\begin{array}<br />1+\frac{Z^{\'\'}_2}{Z^{\'\'}_3} & Z^{\'\'}_2\\<br />\frac{Z^{\'\'}_1+Z^{\'\'}_2+Z^{\'\'}_3}{Z^{\'\'}_1 Z^{\'\'}_3} & 1+\frac{Z^{\'\'}_2}{Z^{\'\'}_1}<br />\end{array}\right]\\<br />\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]&=&\left[\begin{array}<br />1+\frac{\frac{Z^{\'}_2 Z^{\'\'}_2}{Z^{\'}_2+Z^{\'\'}_2}}{\frac{Z^{\'}_3 Z^{\'\'}_3}{Z^{\'}_3+Z^{\'\'}_3}} & \frac{Z^{\'}_2 Z^{\'\'}_2}{Z^{\'}_2+Z^{\'\'}_2}\\<br />\frac{\frac{Z^{\'}_1 Z^{\'\'}_1}{Z^{\'}_1+Z^{\'\'}_1}+\frac{Z^{\'}_2 Z^{\'\'}_2}{Z^{\'}_2+Z^{\'\'}_2}+\frac{Z^{\'}_3 Z^{\'\'}_3}{Z^{\'}_3+Z^{\'\'}_3}}{\frac{Z^{\'}_1 Z^{\'\'}_1}{Z^{\'}_1+Z^{\'\'}_1} \frac{Z^{\'}_3 Z^{\'\'}_3}{Z^{\'}_3+Z^{\'\'}_3}} & 1+\frac{\frac{Z^{\'}_2 Z^{\'\'}_2}{Z^{\'}_2+Z^{\'\'}_2}}{\frac{Z^{\'}_1 Z^{\'\'}_1}{Z^{\'}_1+Z^{\'\'}_1}}<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />1+\frac{\frac{Z^{\'}_2 Z^{\'\'}_2}{Z^{\'}_2+Z^{\'\'}_2}}{\frac{Z^{\'}_3 Z^{\'\'}_3}{Z^{\'}_3+Z^{\'\'}_3}} & \frac{Z^{\'}_2 Z^{\'\'}_2}{Z^{\'}_2+Z^{\'\'}_2}\\<br />\frac{Z^{\'}_1 Z^{\'\'}_1\left(Z^{\'}_3+Z^{\'\'}_3\right)+Z^{\'}_3 Z^{\'\'}_3\left(Z^{\'}_1+Z^{\'\'}_1\right)+\frac{Z^{\'}_2 Z^{\'\'}_2\left(Z^{\'}_1+Z^{\'\'}_1\right)\left(Z^{\'}_3+Z^{\'\'}_3\right)}{Z^{\'}_2+Z^{\'\'}_2}}{Z^{\'}_1 Z^{\'\'}_1 Z^{\'}_3 Z^{\'\'}_3} & 1+\frac{\frac{Z^{\'}_2 Z^{\'\'}_2}{Z^{\'}_2+Z^{\'\'}_2}}{\frac{Z^{\'}_1 Z^{\'\'}_1}{Z^{\'}_1+Z^{\'\'}_1}}<br />\end{array}\right]<br />\end{eqnarray}$ Bに関する予想はあっているが、Cに関してはどうだろう？一見すると似て非なる結果になているが、予想式に小回路の４端子定数をそれぞれ代入して確認してみよう。 $\begin{eqnarray}<br />C&=&C_1+C_2+\frac{\left(A_2-A_1\right)\left(D_1-D_2\right)}{B_1+B_2}\\<br />&=&\frac{Z^{\'}_1+Z^{\'}_2+Z^{\'}_3}{Z^{\'}_1 Z^{\'}_3}+\frac{Z^{\'\'}_1+Z^{\'\'}_2+Z^{\'\'}_3}{Z^{\'\'}_1 Z^{\'\'}_3}+\frac{\left(1+\frac{Z^{\'\'}_2}{Z^{\'\'}_3}-1-\frac{Z^{\'}_2}{Z^{\'}_3}\right)\left(1+\frac{Z^{\'}_2}{Z^{\'}_1}-1-\frac{Z^{\'\'}_2}{Z^{\'\'}_1}\right)}{Z^{\'}_2+Z^{\'\'}_2}\\<br />&=&\frac{\left(Z^{\'}_1+Z^{\'}_2+Z^{\'}_3\right)Z^{\'\'}_1 Z^{\'\'}_3+\left(Z^{\'\'}_1+Z^{\'\'}_2+Z^{\'\'}_3\right)Z^{\'}_1 Z^{\'}_3}{Z^{\'}_1 Z^{\'}_3 Z^{\'\'}_1 Z^{\'\'}_3}+\frac{\left(\frac{Z^{\'}_3 Z^{\'\'}_2-Z^{\'}_2 Z^{\'\'}_3}{Z^{\'}_3 Z^{\'\'}_3}\right)\left(\frac{Z^{\'}_2 Z^{\'\'}_1-Z^{\'}_1 Z^{\'\'}_2}{Z^{\'}_1 Z^{\'\'}_1}\right)}{Z^{\'}_2+Z^{\'\'}_2}\\<br />&=&\frac{Z^{\'}_1 Z^{\'\'}_1\left(Z^{\'}_3+Z^{\'\'}_3\right)+Z^{\'}_3 Z^{\'\'}_3\left(Z^{\'}_1+Z^{\'\'}_1\right)+Z^{\'\'}_1 Z^{\'}_2 Z^{\'\'}_3+Z^{\'}_1 Z^{\'\'}_2 Z^{\'}_3+\frac{\left(Z^{\'}_3 Z^{\'\'}_2-Z^{\'}_2 Z^{\'\'}_3\right)\left(Z^{\'}_2 Z^{\'\'}_1-Z^{\'}_1 Z^{\'\'}_2\right)}{Z^{\'}_2+Z^{\'\'}_2}}{Z^{\'}_1 Z^{\'\'}_1 Z^{\'}_3 Z^{\'\'}_3}\\<br />&=&\frac{Z^{\'}_1 Z^{\'\'}_1\left(Z^{\'}_3+Z^{\'\'}_3\right)+Z^{\'}_3 Z^{\'\'}_3\left(Z^{\'}_1+Z^{\'\'}_1\right)+\frac{\cancel{Z^{\'\'}_1 {Z^{\'}_2}^2 Z^{\'\'}_3}+Z^{\'\'}_1 Z^{\'}_2 Z^{\'\'}_3 Z^{\'\'}_2+Z^{\'}_1 Z^{\'\'}_2 Z^{\'}_3 Z^{\'}_2 +\cancel{Z^{\'}_1 {Z^{\'\'}_2}^2 Z^{\'}_3}+Z^{\'}_3 Z^{\'\'}_2 Z^{\'}_2 Z^{\'\'}_1-\cancel{Z^{\'}_3 {Z^{\'\'}_2}^2 Z^{\'}_1}-\cancel{Z^{\'\'}_3 {Z^{\'}_2}^2 Z^{\'\'}_1}+Z^{\'}_2 Z^{\'\'}_3 Z^{\'}_1 Z^{\'\'}_2}{Z^{\'}_2+Z^{\'\'}_2}}{Z^{\'}_1 Z^{\'\'}_1 Z^{\'}_3 Z^{\'\'}_3}\\<br />&=&\frac{Z^{\'}_1 Z^{\'\'}_1\left(Z^{\'}_3+Z^{\'\'}_3\right)+Z^{\'}_3 Z^{\'\'}_3\left(Z^{\'}_1+Z^{\'\'}_1\right)+\frac{Z^{\'}_2 Z^{\'\'}_2\left(Z^{\'}_1 +Z^{\'\'}_1\right)\left(Z^{\'}_3+Z^{\'\'}_3\right)}{Z^{\'}_2+Z^{\'\'}_2}}{Z^{\'}_1 Z^{\'\'}_1 Z^{\'}_3 Z^{\'\'}_3}<br />\end{eqnarray}$ ということで一見違ってそうに見えて実は一致していた。Maximaではどうにもならなくて手で計算してようやく式が同じであることを確認した。さてあとA,Dだが相反回路ではAD-BC=1が成り立つので３つがわかれば残り一個は自動的に決まる。ちょうど仏典の般若心経に出てくる六波羅蜜のうｃい５つを得ると最後の一つ（智慧波羅蜜）が自動的に得られる（修行が完成する）というのと似ている。波羅蜜は仏典の原語であるサンスクリット語पारमिता Pāramitā パラミータにあてた漢字であるが、パラメータと良く似ている（全然意味が違うが）。４つのパラメータのうち３つを得ると残りは自動的に得られるという。なんとなく仏典には数学的なものを感じる。実際読んでみると証明論理的な記述もあったりして驚かされる。残念ながらホテルとかに置いてある仏典集の日本語文を読んでいていつくも意味不明な文があり、対訳の英文を読んだら明快明瞭、日本語の訳が基本的な誤訳か不適切な文になっているだけだった。おろらく英文がオリジナルで、それを日本語訳した人が英語を良く解っていなかったのだろう。英文でwithoutが使われている部分の訳が「煩悩なくして悟りを得ることはなかったのである」とでもすればわかるものを「煩悩はなく悟りもなかったのである」としてある辺りがひどすぎる。何の話しだったっけ。ああ、AとDね。もうひとつのケースを考えてみよう。それはLattice回路である。全体の回路の４端子定数は $\begin{eqnarray}<br />\left[\begin{array}<br />A_1 & B_1\\<br />C_1 & D_1<br />\end{array}\right]&=&\left[\begin{array}<br />1 & 2 Z_1\\<br />0 & 1<br />\end{array}\right]\\<br />\left[\begin{array}<br />A_2 & B_2\\<br />C_2 & D_2<br />\end{array}\right]&=&\left[\begin{array}<br />-1 & -2 Z_2\\<br />0 & -1<br />\end{array}\right]\\<br />\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]&=&\left[\begin{array}<br />\frac{1}{\frac{Z_2}{Z_1+Z_2}-\frac{Z_1}{Z_1+Z_2}} & \frac{1}{\frac{1}{2 Z_1}+\frac{1}{2 Z_2}}\\<br />\frac{1}{\frac{Z_2}{2}-\frac{Z_1}{2}} & \frac{\frac{1}{2 Z_1}+\frac{1}{2 Z_2}}{\frac{1}{2 Z_1}-\frac{1}{2 Z_2}}<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />\frac{Z_1+Z_2}{Z_2-Z_1} & \frac{2 Z_1 Z_2}{Z_1+Z_2}\\<br />\frac{2}{Z_2-Z_1} & \frac{Z_1+Z_2}{Z_2-Z_1}<br />\end{array}\right]<br />\end{eqnarray}$ 各４端子定数は電流分流則や電圧分圧則、重ね合わせの理を駆使して導いた。回路への入力電圧は同じで、電流が２つの回路に分かれ、出力側では電圧が同じで電流が合流するとわかれば比較的簡単である。そこからひとつの重要なヒントが得られた気がする。このLattice回路のケースとと前出のπ形回路のケースからA,Dに関してAはA1,A2,B1,B2の内容に、DはD1,D2,B1,B2の内容に依存する事実から最終的に以下の予想を導くことができる $\begin{eqnarray}<br />A&=&\frac{A_1 B_2+A_2 B_1}{B_1+B_2}\\<br />B&=&\frac{B_1 B_2}{B_1+B_2}\\<br />C&=&C_1+C_2+\frac{\left(A_2-A_1\right)\left(D_1-D_2\right)}{B_1+B_2}\\<br />D&=&\frac{D_1 B_2+D_2 B_1}{B_1+B_2}<br />\end{eqnarray}$ さてあとは証明するだけだ。Lattice回路のケースで気づいたヒントを元に、最初の線形代数によるアプローチを少し改良すれば見えてきそうである。命題を整理すると。以下の既知の４端子定数を持つ２つの小回路を並列接続した場合 $\begin{eqnarray}<br />\left[\begin{array}<br />E^{\'}_1\\<br />I^{\'}_1<br />\end{array}\right]&=&\left[\begin{array}<br />A_1 & B_1\\<br />C_1 & D_1<br />\end{array}\right]\left[\begin{array}<br />E^{\'}_2\\<br />I^{\'}_2<br />\end{array}\right]\\<br />\left[\begin{array}<br />E^{\'\'}_1\\<br />I^{\'\'}_1<br />\end{array}\right]&=&\left[\begin{array}<br />A_2 & B_2\\<br />C_2 & D_2<br />\end{array}\right]\left[\begin{array}<br />E^{\'\'}_2\\<br />I^{\'\'}_2<br />\end{array}\right]<br />\end{eqnarray}$ 全体の回路の４端子定数は以下の様に一意に定まる。 $\begin{eqnarray}<br />\left[\begin{array}<br />E_1\\<br />I_1<br />\end{array}\right]&=&\left[\begin{array}<br />A & B\\<br />C & D<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />I_2<br />\end{array}\right]\\<br />&=&\left[\begin{array}<br />\frac{A_1 B_2+A_2 B_1}{B_1+B_2} & \frac{B_1 B_2}{B_1+B_2}\\<br />C_1+C_2+\frac{\left(A_2-A_1\right)\left(D_1-D_2\right)}{B_1+B_2} & \frac{D_1 B_2+D_2 B_1}{B_1+B_2}<br />\end{array}\right]\left[\begin{array}<br />E_2\\<br />I_2<br />\end{array}\right]<br />\end{eqnarray}$ さて振り出しに戻って線形代数的手法でこれを証明することにしよう。それに先だって線形代数をちょっと勉強してくる(;´Д`) なにもそこまでしてというかもしれないが、粘着気質なのでなかなか諦められない。おそらくどっかの本にずばり同じような問題が扱われているということは期待できないだろう。自分で考えるしかない。ひとつの可能性は著者のように一度Y行列に変換して重ね合わせた後、再びF行列に戻すというのを途中Y行列を経由せずともショートカットして重ね合わせの理でF行列のまま導出できないかというもの。いちど全体の流れを描いてみて、ショートカットできる可能性を探るという手もある。I1=I1'+I1'',I2=I2'+I2''、E1=E1/2+E1/2,E2=E2/2+E2/2という風にすれば２つの電流源か２つの電圧源の重ね合わせと考えることもできる。これがヒントなのだが、そこから先が見通しがつかない。もうひとつはまだ知らない線形代数理論がうまく当てはまる可能性。最悪は前者でお茶を濁すことになりそう。手元の参考書で他にこれと同じ問題の解を示しているのは電気書院「電気回路」大坪昭著のみで、行列表記を一切使わず４端子定数による回路方程式から部分回路に流れる端子対電流をもとめ、それらから全体の回路の端子対を流れる電流(I1=I1'+I1'',I2=I2'+I2'')を重ね合わせの理で導き全体の４端子定数を簡潔に求めている。行列を使わない方が簡潔だ。それでもステップとしては複数段あるので見通しが良くない。そこで思いついたのが、それとも違う独自のアプローチ。なんのことはない、今まで部分回路側からボトムアップでアプローチしようとして挫折していたのだが、ふと全体回路からトップダウンで下りてくれば見通しよく証明できることに気づいた。やってみたらうまくいった。基本的に全体回路をアドミッタンス行列表現に直すと、部分回路も４端子定数で与えられているので、すぐに全体のアドミッタンス行列が求まる。それを４端子定数に変換するだけである。まず回路全体のアドミッタンス行列を以下のように導く $\begin{eqnarray}<br />X&=&\left[\begin{array}E_1\\E_2\end{array}\right]\\<br />Y&=&\left[\begin{array}I_1\\-I_2\end{array}\right]\\<br />P&=&\left[\begin{array}E_2\\I_2\end{array}\right]=\left[\begin{array}0&1\\0&0\end{array}\right]X+\left[\begin{array}0&0\\0&-1\end{array}\right]Y\\<br />Q&=&\left[\begin{array}E_1\\I_1\end{array}\right]=\left[\begin{array}1&0\\0&0\end{array}\right]X+\left[\begin{array}0&0\\1&0\end{array}\right]Y\\<br />&=&\left[\begin{array}A&B\\C&D\end{array}\right]P\\<br />&=&\left[\begin{array}A&B\\C&D\end{array}\right]\left(\left[\begin{array}0&1\\0&0\end{array}\right]X+\left[\begin{array}0&0\\0&-1\end{array}\right]Y\right)\\<br />&&\left(\left[\begin{array}0&0\\1&0\end{array}\right]-\left[\begin{array}A&B\\C&D\end{array}\right]\left[\begin{array}0&0\\0&-1\end{array}\right]\right)Y=\left(\left[\begin{array}A&B\\C&D\end{array}\right]\left[\begin{array}0&1\\0&0\end{array}\right]-\left[\begin{array}1&0\\0&0\end{array}\right]\right)X\\<br />Y&=&\left(\left[\begin{array}0&0\\1&0\end{array}\right]-\left[\begin{array}A&B\\C&D\end{array}\right]\left[\begin{array}0&0\\0&-1\end{array}\right]\right)^{-1}\left(\left[\begin{array}A&B\\C&D\end{array}\right]\left[\begin{array}0&1\\0&0\end{array}\right]-\left[\begin{array}1&0\\0&0\end{array}\right]\right)X\\<br />&=&\left(\left[\begin{array}0&0\\1&0\end{array}\right]-\left[\begin{array}0&B\\0&D\end{array}\right]\right)^{-1}\left(\left[\begin{array}0&A\\0&C\end{array}\right]-\left[\begin{array}1&0\\0&0\end{array}\right]\right)X\\<br />&=&\left[\begin{array}0&-B\\1&-D\end{array}\right]^{-1}\left[\begin{array}-1&A\\0&C\end{array}\right]X\\<br />&=&\left[\begin{array}-\frac{D}{B}&1\\ \frac{1}{B}&0\end{array}\right]\left[\begin{array}-1&A\\0&C\end{array}\right]X\\<br />&=&\left[\begin{array}\frac{D}{B}&C-\frac{A D}{B}\\-\frac{1}{B}&\frac{A}{B}\end{array}\right]X\\<br />&=&\left(\left[\begin{array}\frac{D_1}{B_1}&C_1-\frac{A_1 D_1}{B_1}\\-\frac{1}{B_1}&\frac{A_1}{B_1}\end{array}\right]+\left[\begin{array}\frac{D_2}{B_2}&C_2-\frac{A_2 D_2}{B_2}\\-\frac{1}{B_2}&\frac{A_2}{B_2}\end{array}\right]\right)X\\<br />&=&\left[\begin{array}\frac{D_1}{B_1}+\frac{D_2}{B_2}&C_1+C_2-\frac{A_1 D_1}{B_1}-\frac{A_2 D_2}{B_2}\\-\frac{1}{B_1}-\frac{1}{B_2}&\frac{A_1}{B_1}+\frac{A_2}{B_2}\end{array}\right]X\\<br />&=&\left[\begin{array}Y_{11}&Y_{12}\\Y_{21}&Y_{22}\end{array}\right]X<br />\end{eqnarray}$ 最後に上記で導いた回路全体のアドミッタンス行列を回路全体の４端子定数に変換すると $\begin{eqnarray}<br />X&=&\left[\begin{array}1&0\\0&0\end{array}\right]Q+\left[\begin{array}0&0\\1&0\end{array}\right]P\\<br />Y&=&\left[\begin{array}0&1\\0&0\end{array}\right]Q+\left[\begin{array}0&0\\0&-1\end{array}\right]P\\<br />Y&=&\left[\begin{array}Y_{11}&Y_{12}\\Y_{21}&Y_{22}\end{array}\right]X\\<br />&=&\left[\begin{array}\frac{D_1}{B_1}+\frac{D_2}{B_2}&C_1+C_2-\frac{A_1 D_1}{B_1}-\frac{A_2 D_2}{B_2}\\-\frac{1}{B_1}-\frac{1}{B_2}&\frac{A_1}{B_1}+\frac{A_2}{B_2}\end{array}\right]X\\<br />&=&\left[\begin{array}\frac{D_1}{B_1}+\frac{D_2}{B_2}&C_1+C_2-\frac{A_1 D_1}{B_1}-\frac{A_2 D_2}{B_2}\\-\frac{1}{B_1}-\frac{1}{B_2}&\frac{A_1}{B_1}+\frac{A_2}{B_2}\end{array}\right]\left(\left[\begin{array}1&0\\0&0\end{array}\right]Q+\left[\begin{array}0&0\\1&0\end{array}\right]P\right)\\<br />&&\left(\left[\begin{array}0&1\\0&0\end{array}\right]-\left[\begin{array}\frac{D_1}{B_1}+\frac{D_2}{B_2}&C_1+C_2-\frac{A_1 D_1}{B_1}-\frac{A_2 D_2}{B_2}\\-\frac{1}{B_1}-\frac{1}{B_2}&\frac{A_1}{B_1}+\frac{A_2}{B_2}\end{array}\right]\left[\begin{array}1&0\\0&0\end{array}\right]\right)Q=\left(\left[\begin{array}\frac{D_1}{B_1}+\frac{D_2}{B_2}&C_1+C_2-\frac{A_1 D_1}{B_1}-\frac{A_2 D_2}{B_2}\\-\frac{1}{B_1}-\frac{1}{B_2}&\frac{A_1}{B_1}+\frac{A_2}{B_2}\end{array}\right]\left[\begin{array}0&0\\1&0\end{array}\right]-\left[\begin{array}0&0\\0&-1\end{array}\right]\right)P\\<br />Q&=&\left(\left[\begin{array}0&1\\0&0\end{array}\right]-\left[\begin{array}\frac{D_1}{B_1}+\frac{D_2}{B_2}&C_1+C_2-\frac{A_1 D_1}{B_1}-\frac{A_2 D_2}{B_2}\\-\frac{1}{B_1}-\frac{1}{B_2}&\frac{A_1}{B_1}+\frac{A_2}{B_2}\end{array}\right]\left[\begin{array}1&0\\0&0\end{array}\right]\right)^{-1}\left(\left[\begin{array}\frac{D_1}{B_1}+\frac{D_2}{B_2}&C_1+C_2-\frac{A_1 D_1}{B_1}-\frac{A_2 D_2}{B_2}\\-\frac{1}{B_1}-\frac{1}{B_2}&\frac{A_1}{B_1}+\frac{A_2}{B_2}\end{array}\right]\left[\begin{array}0&0\\1&0\end{array}\right]-\left[\begin{array}0&0\\0&-1\end{array}\right]\right)P\\<br />&=&\left[\begin{array}-\frac{D_2}{B_2}-\frac{D_1}{B_1}&1\\ \frac{1}{B_2}+\frac{1}{B_1}&0\end{array}\right]^{-1}\left[\begin{array}-\frac{A_2 D_2}{B_2}-\frac{A_1 D_1}{B_1}+C_2+C_1&0\\ \frac{A_2}{B_2}+\frac{A_1}{B_1} & 1\end{array}\right]P\\<br />&=&\left[\begin{array}0 & -\frac{1}{-\frac{1}{B_2}-\frac{1}{B_1}}\\ 1 & \frac{-\frac{D_2}{B_2}-\frac{D_1}{B_1}}{-\frac{1}{B_2}-\frac{1}{B_1}}\end{array}\right]\left[\begin{array}-\frac{A_2 D_2}{B_2}-\frac{A_1 D_1}{B_1}+C_2+C_1&0\\ \frac{A_2}{B_2}+\frac{A_1}{B_1} & 1\end{array}\right]P\\<br />&=&\left[\begin{array}-\frac{\frac{A_2}{B_2}+\frac{A_1}{B_1}}{-\frac{1}{B_2}-\frac{1}{B_1}} & -\frac{1}{-\frac{1}{B_2}-\frac{1}{B_1}}\\ \frac{\left( \frac{A_2}{B_2}+\frac{A_1}{B_1}\right) \left( -\frac{D_2}{B_2}-\frac{D_1}{B_1}\right) }{-\frac{1}{B_2}-\frac{1}{B_1}}-\frac{A_2 D_2}{B_2}-\frac{A_1 D_1}{B_1}+C_2+C_1 & \frac{-\frac{D_2}{B_2}-\frac{D_1}{B_1}}{-\frac{1}{B_2}-\frac{1}{B_1}}\end{array}\right]P\\<br />&=&\left[\begin{array}\frac{A_1 B_2+A_2 B_1}{B_2+B_1} & \frac{B_1 B_2}{B_2+B_1}\\ C_1+C_2+\frac{\left( A_2-A_1\right) \left( D_1-D_2\right) }{B_2+B_1} & \frac{B_1 D_2+B_2 D_1}{B_2+B_1}\end{array}\right]P\\<br />&=&\left[\begin{array}A&B\\C&D\end{array}\right]P<br />\end{eqnarray}$ ということになる。 Q.E.D P.S すくなくとも著者のよりは見通しが良い。一見も面倒そうに見えるが行列の計算はよく見れば単純なものばかりだった。各変換の前半部分に頻繁に現れる2行２列の定係数行列は線形代数ではなんと呼ぶのだろう？　パラメータ間変換公式に代入する方法よりも線形代数を使った方がはるかに簡単で間違いなくパラメータ変換ができる。何よりも変換公式を完全に忘れてしまっていても良いのが嬉しい。少なくともこの方法によるパラメータ変換はどの参考書やインターネット上でも見かけない。もしかしてオリジナルかもしれないし、単に誰もやろうとしないアホな方法かもしれない。後者の様な気がする(;´Д`) P.S 証明の前半で回路全体のアドミッタンスパラメータを導いた段階で以下の関係が得られていることを賢明な読者は見逃さないだろう。 $\begin{eqnarray}<br />\left[\begin{array}\frac{D}{B}&C-\frac{A D}{B}\\-\frac{1}{B}&\frac{A}{B}\end{array}\right]&=&\left[\begin{array}\frac{D_1}{B_1}+\frac{D_2}{B_2}&C_1+C_2-\frac{A_1 D_1}{B_1}-\frac{A_2 D_2}{B_2}\\-\frac{1}{B_1}-\frac{1}{B_2}&\frac{A_1}{B_1}+\frac{A_2}{B_2}\end{array}\right]<br />\end{eqnarray}$ これをA,B,C,Dに関する４元連立方程式として解けば同じ結果が得られる。以前の問題にも出くわしたように二次形式が伴うので手計算で解くのは意外に大変であるが、その確認は読者の課題としよう(´∀` )。証明の後半はその方程式を解いているのに等しい。代数的に面白い関係である。 P.S 手元の古書を眺めていたら以前も紹介した「回路網理論I」尾崎弘、黒田一之著の付録A-4 "２端子対回路と４次元ベクトル"に同じ様なことが書かれていた。Vitold Belevitchが1954年6月号のIRE. Transactions on Circuit Theory, Vol CT-4 P.P. 105-111で発表したと出典がある。ページにはこの本の以前の持ち主だった人が油紙のしおりを差し込んである。特別目をひいた内容だったのかもしれない。確かに他では見たことがない。V. Belevitchは卓越した数学的観点での回路網理論や多方面の研究で業績があった人のようだ。Cauerと同時代の人で戦後Cauerの功績を広めたことでも知られる。歴史的に二端子対回路を最初に考えたのは Franz Breisigであることを見いだしたのは彼である。数え上げればきりがない。ちょっと教わりたかった気がする。生まれるのがあまりにも遅すぎた。せめて回路網理論のバイブルである著書の"Classical Network Theory"を読んでみたい。入手困難だが。こちらも遅ればせながら独自に同じ着想に到達したというだけで満足である。

webadm	投稿日時: 2010-6-3 12:42
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3090	アドミッタンスパラメータ次ぎの問題は下記の回路のアドミッタンスパラメータを求めよというもの。普通にアドミッタンスパラメータの条件を適用して駆動点アドミッタンスや伝達アドミッタンスを解析して求めるのは既にこの規模の回路で大変である。従って部分回路に分けてそれらの並列接続として全体回路のアドミッタンスパラメータを求めるのが簡単である。著者とは異なる部分回路構成でやってみよう。既にこれまでの問題で登場した３種類の部分回路の並列接続として考える。それぞれの部分回路のアドミッタンス行列は $\begin{eqnarray}<br />Y^{\'}&=&\left[\begin{array}\frac{1}{Z_2}&-\frac{1}{Z_2}\\-\frac{1}{Z_2}&\frac{1}{Z_2}\end{array}\right]\\<br />Y^{\'\'}&=&\left[\begin{array}\frac{1}{Z_1}&0\\0&\frac{1}{Z_3}\end{array}\right]\\<br />Y^{\'\'\'}&=&\left[\begin{array}\frac{Z_5+Z_6}{Z_4 Z_5+Z_4 Z_6+Z_5 Z_6}&-\frac{Z_5}{Z_4 Z_5+Z_4 Z_6+Z_5 Z_6}\\-\frac{Z_5}{Z_4 Z_5+Z_4 Z_6+Z_5 Z_6}&\frac{Z_4+Z_5}{Z_4 Z_5+Z_4 Z_6+Z_5 Z_6}\end{array}\right]<br />\end{eqnarray}$ 従って回路全体のアドミッタンス行列は $\begin{eqnarray}<br />Y&=&Y^{\'}+Y^{\'\'}+Y^{\'\'\'}\\<br />&=&\left[\begin{array}\frac{1}{Z_2}&-\frac{1}{Z_2}\\-\frac{1}{Z_2}&\frac{1}{Z_2}\end{array}\right]+\left[\begin{array}\frac{1}{Z_1}&0\\0&\frac{1}{Z_3}\end{array}\right]+\left[\begin{array}\frac{Z_5+Z_6}{Z_4 Z_5+Z_4 Z_6+Z_5 Z_6}&-\frac{Z_5}{Z_4 Z_5+Z_4 Z_6+Z_5 Z_6}\\-\frac{Z_5}{Z_4 Z_5+Z_4 Z_6+Z_5 Z_6}&\frac{Z_4+Z_5}{Z_4 Z_5+Z_4 Z_6+Z_5 Z_6}\end{array}\right]\\<br />&=&\left[\begin{array}\frac{1}{Z_1}+\frac{1}{Z_2}+\frac{Z_5+Z_6}{Z_4 Z_5+Z_4 Z_6+Z_5 Z_6}&-\left(\frac{1}{Z_2}+\frac{Z_5}{Z_4 Z_5+Z_4 Z_6+Z_5 Z_6}\right)\\-\left(\frac{1}{Z_2}+\frac{Z_5}{Z_4 Z_5+Z_4 Z_6+Z_5 Z_6}\right)&\frac{1}{Z_2}+\frac{1}{Z_3}+\frac{Z_4+Z_5}{Z_4 Z_5+Z_4 Z_6+Z_5 Z_6}\end{array}\right]<br />\end{eqnarray}$ ということになる。

webadm	投稿日時: 2010-6-5 13:04
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3090	まだまだ：４端子定数次ぎも４端子定数の問題。理論の時にやった気もするが、４端子定数A,B,C,Dで表される２端子対回路の入出力を入れ替えた場合に４端子定数がD,B,C,Aとなることを証明せよというもの。電流の極性の違いに注意すれば、I1=-I1',I2=-I2'であり、また線形受動回路ではAD-BC=1であることから $\begin{eqnarray}<br />P^{\'}&=&\left[\begin{array}E_1\\I^{\'}_1\end{array}\right]\\<br />Q^{\'}&=&\left[\begin{array}E_2\\I^{\'}_2\end{array}\right]\\<br />P&=&\left[\begin{array}E_2\\I_2\end{array}\right]=\left[\begin{array}1&0\\0&-1\end{array}\right]Q^{\'}\\<br />Q&=&\left[\begin{array}E_1\\I_1\end{array}\right]=\left[\begin{array}1&0\\0&-1\end{array}\right]P^{\'}\\<br />Q&=&\left[\begin{array}A&B\\C&D\end{array}\right]P\\<br />\left[\begin{array}1&0\\0&-1\end{array}\right]P^{\'}&=&\left[\begin{array}A&B\\C&D\end{array}\right]\left[\begin{array}1&0\\0&-1\end{array}\right]Q^{\'}\\<br />Q^{\'}&=&\left(\left[\begin{array}A&B\\C&D\end{array}\right]\left[\begin{array}1&0\\0&-1\end{array}\right]\right)^{-1}\left[\begin{array}1&0\\0&-1\end{array}\right]P^{\'}\\<br />&=&\left[\begin{array}A & -B\\C & -D\end{array}\right]^{-1}\left[\begin{array}1&0\\0&-1\end{array}\right]P^{\'}\\<br />&=&\left[\begin{array}-\frac{D}{B C-A D} & \frac{B}{B C-A D}\\-\frac{C}{B C-A D} & \frac{A}{B C-A D}\end{array}\right]\left[\begin{array}1&0\\0&-1\end{array}\right]P^{\'}\\<br />&=&\left[\begin{array}\frac{D}{A D-B C} & \frac{B}{A D-B C}\\ \frac{C}{A D-B C} & \frac{A}{A D-B C}\end{array}\right]P^{\'}\\<br />&=&\left[\begin{array}D&B\\C&A\end{array}\right]P^{\'}<br />\end{eqnarray}$ Q.E.D

webadm	投稿日時: 2010-6-5 13:44
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3090	影像パラメータと４端子定数次ぎの問題は影像パラメータと４端子定数の関係式を導出せよというもの。すなわち２端子対回路の影像パラメータを４端子定数で、また逆に４端子定数を影像パラメータでそれぞれ表せという意味になる。理論の時にも一度やったが見通しが悪かったので、見通しの良い線形代数的手法で再挑戦してみよう。理論の時に一通り導いたはずだが、別のやり方で同じ結果を導こうとすると実は良く解っていなかったということが判明する。前にやったやり方は理解していてすぐ同じように導出できるのだが、解っていないというのは、それが数学の対象としてどんな扱いになるのかという点である。別のやり方を考える場合にそれが解っていないと致命的である。影像パラメータは２つの影像インピーダンスと伝達定数の３つから成るが、４端子定数が変わればそれに依存して変わっていく、それは数学的対象として見た場合に４端子定数に対して幾何学的に何に相当するのかという点である。確かに影像インピーダンスも伝達定数も定数であり複素数であるのでベクトルとしても良いが、それら解の集合が存在する代数多様体はどんな形をしているのかといった点である。実はそんなことが解っていなかったというか知ろとしてなかったのである。単純に電気回路の基礎知識というのであればそんなことは気にせずに試験問題のパターンを暗記して短時間に答えを見いだせばよいのだが、実務で今まで誰も考えたことのないような視点で考え直す必要が生じる場合にはそういったスキルは微塵も役にたたない。理数系の人は本質を見抜くことに徹して、応用や重箱の隅（境界領域）の問題には興味を示さない。工学系は応用と重箱の隅が死活問題なのとは大違い。それだからこそ工学系も本質を見抜く力がないと袋小路に陥って抜け出せなくなる。要は影像パラメータの数学的な本質を知らないと見通しの良い形で関係式を導出することはできないということであった。この件についてはまだ時間を要するので、先に残りの問題をしばらく並行して進めることにする。これは試験問題ではないので、時間的な制約は設ける必要がないのである。いずれにしても線形代数的手法は信号処理や先端の工学理論ではもはや避けて通れないため身に付ける必要がある。したがって「理論の時にやってしまったので割愛する」ということでお茶を濁すことにはしたくないつもりである。ようやく光明が見えた(2010/06/08) 数学者は問題解決の経緯を明かすことめったにないが、ここはおもちゃ箱なので経緯も楽しむ。最初に上の図の回路を以下の様に行列表記をしてみることからはじめよう。 $\begin{eqnarray}<br />Q=\left[\begin{array}E_1\\I_1\end{array}\right]&=&\left[\begin{array}Z_{01}I_1\\I_1\end{array}\right]=I_1\left[\begin{array}Z_{01}\\1\end{array}\right]\\<br />P=\left[\begin{array}E_2\\I_2\end{array}\right]&=&\left[\begin{array}Z_{02}I_2\\I_2\end{array}\right]=I_2\left[\begin{array}Z_{02}\\1\end{array}\right]\\<br />Q&=&\left[\begin{array}A&B\\C&D\end{array}\right]P\\<br />I_1\left[\begin{array}Z_{01}\\1\end{array}\right]&=&I_2\left[\begin{array}A&B\\C&D\end{array}\right]\left[\begin{array}Z_{02}\\1\end{array}\right]<br />\end{eqnarray}$ しかしひとつの式にZ01,Z02,I1,I2と４つの不定元を含むので結局行列を展開して以前やったようにZ01=E1/I1,Z02=E2/I2の式に代入して連立方程式として別途解くということになってしまう。これでは何も変わらない。一発でZ01なりZ02を見いだすアプローチはないものか。ここ数日の間、新しく購入した線形代数のテキストを読んだり、YoutubeでMITやインドの大学の線形代数の講義を眺めたりしているうちに今朝名案を思いついた。最初からZ01、Z02の片方を消去する方法があった。それは先の二端子対回路の入出力方向をひっくり返した鏡像回路を元の２端子回路に縦続接続すれば両端の影像インピーダンスがZ01になる。２つの二端子対回路を更にひっくり返せば両端の影像インピーダンスがZ02になる。これで式を立てればZ01かZ02のいずれかしか現れないことになる。図で表すとやってみよう、二端子対回路の鏡像回路の４端子定数はAとDが逆になるだけなので $\begin{eqnarray}<br />Q=\left[\begin{array}E_1\\I_1\end{array}\right]&=&\left[\begin{array}Z_{01}I_1\\I_1\end{array}\right]=I_1\left[\begin{array}Z_{01}\\1\end{array}\right]=E_1\left[\begin{array}1\\\frac{1}{Z_{01}}\end{array}\right]\\<br />P=\left[\begin{array}E_2\\I_2\end{array}\right]&=&\left[\begin{array}Z_{01}I_2\\I_2\end{array}\right]=I_2\left[\begin{array}Z_{01}\\1\end{array}\right]=E_2\left[\begin{array}1\\\frac{1}{Z_{01}}\end{array}\right]\\<br />Q&=&\left[\begin{array}A&B\\C&D\end{array}\right]\left[\begin{array}D&B\\C&A\end{array}\right]P\\<br />E_1\left[\begin{array}1\\\frac{1}{Z_{01}}\end{array}\right]&=&E_2\left[\begin{array}A&B\\C&D\end{array}\right]\left[\begin{array}D&B\\C&A\end{array}\right]\left[\begin{array}1\\\frac{1}{Z_{01}}\end{array}\right]\\<br />\left[\begin{array}A D+B C & 2 A B\\ 2 C D & A D+B C\end{array}\right]\left[\begin{array}1\\\frac{1}{Z_{01}}\end{array}\right]&=&\frac{E_1}{E_2}\left[\begin{array}1\\\frac{1}{Z_{01}}\end{array}\right]\\<br />Lx&=&\lambda x,\,\,x\ne0\\<br />L&=&\left[\begin{array}A D+B C & 2 A B\\ 2 C D & A D+B C\end{array}\right]\\<br />x&=&\left[\begin{array}1\\\frac{1}{Z_{01}}\end{array}\right]<br />\end{eqnarray}$ ということになる。これは線形代数の固有値ー固有ベクトル方程式(eigenvalue-eigenvector equation) である $\begin{eqnarray}<br />L x&=&\lambda x,\,\,x\ne0<br />\end{eqnarray}$ 影像インピーダンスを求める問題は固有ベクトル(eigenvector)を求める問題だったわけである。それを最初に教えてくれれば面倒くさい導出手順を暗記しなくて済むものを。ほとんどの電気回路理論の教科書がこの事実を言及しない(1)のはただでさえ難解な線形代数とつながってしまうと学生がついてこれなくなることを恐れてのことだろう。確かに学生の頃に線形代数は数学のカリキュラムに入っていたはずだが、準備的な行列と行列式の部分しか記憶に残っていない。固有値と固有ベクトルを身近に感じたのは今朝この発見が生まれて初めてだ。まあ固有値問題や固有ベクトル（主成分とかスペクトルとも呼ばれる）問題は最先端の工学領域ではありとあらゆるところに存在するので避けて通れない（Googleの検索エンジンの中心にあるPageRankアルゴリズムも固有ベクトル問題の一種のソルバーらしい）。最先端理論を必要としない業務にはそれらは既に解かれているので直面することはない。線形代数の主題はこの固有値ー固有ベクトル問題なのだが、それを学ぶための準備で大半の時間が費やされてしまって固有値ー固有ベクトル問題にたどり着かないか、最期の講義時間でちょっと出てくる程度だったりする。数学の授業は歴史的な順番ではなく構造的な順番で教えることになるので主題は一番最期に登場する（あるいは時間切れでそこまで進まずに終わってしまう）ことになる。本当は歴史を辿る意味で問題が先にあって、先人がどのようにそれを攻略していったかというのを学ぶやり方もあるのではないかと思う。いずれ別の機会に紹介するが、最近読んでいる線形代数のテキストはちくま学芸文庫からつい先日復刻されたSerge Langの「ラング線形代数学（上）（下）」である。注文して届いたら文庫本サイズで電車の中やホームでも立ったままいつでも読めるのが嬉しい。それと線形代数の本ではないが岩波文庫にある高木貞治の「近世数学史談」も文庫本なのでずっと持ち歩いて面白く何度も読み返している。高木貞治は数学歴史話の講談師のごとく、まるで１８世紀や１９世紀の西欧の数学界を見てきたような語り口で生き生きと伝えている（高木貞治は事実戦前ドイツの最先端数学界隈に居て西洋数学の血脈を受け継いで日本に帰国した人と言える）。読む物を１９世紀にタイムワープして大数学者と隣り合わせて居るような不思議な体験をさせてくれる。名作で抱腹絶倒、涙無くして読めないそんな本である。かのフェルマー予想を解く鍵となった谷山・志村予想に名を残す谷山豊はこの本を読んだことから数学者を志したらしい。なんの話しだったったけ。ああ線形代数のテキストね。というわけで市販の入門書では上記の固有値ー固有ベクトル方程式を解く方法についてはページを割いていない。実はこの分野は未だに終わっていない分野ですべてを書ききれない程ある。固有値問題についてはそれだけのために書かれた専門書がまた別にある。当然ながらそれらも入手済みであるが、紹介はまた別の機会にしよう。さて次ぎは先の方程式を解いて固有ベクトルの値であるZ01を求めなければならない。線形代数まだ勉強中なのに、どうすんだこれ(;´Д`) 実はMaximaには変換行列を与えれば固有値ー固有ベクトル方程式を解いてくれる機能が備わっている。実際にやってみると $\begin{verbatim}<br />matrix([A,B],[C,D]).matrix([D,B],[C,A]);<br />\end{verbatim}\\<br />\left[\begin{array}A D+B C & 2 A B\\ 2 C D & A D+B C\end{array}\right]\\<br />\begin{verbatim}<br />eigenvectors(%);<br />\end{verbatim}<br />\left[\left[\left[-2 \sqrt{A B C D}+A D+B C,2 \sqrt{A B C D}+A D+B C\right],\left[1,1\right]\right],\left[1,-\frac{\sqrt{A B C D}}{A B}\right],\left[1,\frac{\sqrt{A B C D}}{A B}\right]\right]$ 結果の最初の２つは固有値を表し、次ぎの２つがその多重度、それに固有値に対する固有ベクトルが並んでいる。固有ベクトルは２つあるが、線形受動回路ではZ01の実数部が常に正の値であることから、 $\begin{eqnarray}<br />\left[1,\frac{\sqrt{A B C D}}{A B}\right]&=&\left[1,\sqrt{\frac{ C D}{A B}}\right]=\left[1,\frac{1}{Z_{01}}\right]<br />\end{eqnarray}$ ということになる。従ってZ01は $\begin{eqnarray}<br />Z_{01}&=&\sqrt{\frac{A B}{ C D}}<br />\end{eqnarray}$ と導かれる。またこの時の固有値に注目すると $\begin{eqnarray}<br />2\theta&=&\ln \lambda=\ln\left(2 \sqrt{A B C D}+A D+B C\right)\\<br />&=&\ln\left(\sqrt{A D}+\sqrt{B C}\right)^2\\<br />&=&2\ln\left(\sqrt{A D}+\sqrt{B C}\right)<br />\theta&=&\ln\left(\sqrt{A D}+\sqrt{B C}\right)<br />\end{eqnarray}$ つまり伝達定数を求める問題は固有値を求める問題である。すなわち影像パラメータを求める問題は固有値ー固有ベクトル問題に帰着する。 Z02についても変換行列の順序を交換すればよいので $\begin{verbatim}<br />matrix([D,B],[C,A]).matrix([A,B],[C,D]);<br />\end{verbatim}\\<br />\left[\begin{array}A D+B C & 2 B D\\ 2 A C & A D+B C\end{array}\right]\\<br />\begin{verbatim}<br />eigenvectors(%);<br />\end{verbatim}<br />\left[\left[\left[-2 \sqrt{A B C D}+A D+B C,2 \sqrt{A B C D}+A D+B C\right],\left[1,1\right]\right],\left[1,-\frac{\sqrt{A B C D}}{B D}\right],\left[1,\frac{\sqrt{A B C D}}{B D}\right]\right]$ $\begin{eqnarray}<br />\left[1,\frac{\sqrt{A B C D}}{B D}\right]&=&\left[1,\sqrt{\frac{ A C}{B D}}\right]=\left[1,\frac{1}{Z_{02}}\right]<br />\end{eqnarray}$ 従ってZ02は $\begin{eqnarray}<br />Z_{02}&=&\sqrt{\frac{B D}{ A C}}<br />\end{eqnarray}$ ということになる。なんだ簡単じゃないか(´∀` ) これだとMaximaがどうやって固有値や固有ベクトルを導いているか皆目わからないので、先の固有ベクトル方程式を自分で解いてみよう。それに先だって線形代数を固有値問題まで勉強しないと(;´Д`) 固有値問題は数学的にはかなり事前準備と関連定理や補題が山ほどあるので後回しにして、他に発見された重要な事実について述べておく。・非対称な二端子対回路をその鏡像回路と縦続接続すると全体としては対称な二端子対回路になる。・この対称な二端子対回路の両端の影像インピーダンスは反復インピーダンスそのものである。・縦続接続された二端子対回路が対称回路なら対称回路を縦続接続しても対称な二端子対回路になるから伝搬定数は元の二端子回路の伝搬定数の２倍になる（非対称の場合には２つの異なる方向の伝達定数の和となるのでその平均値が伝達定数となる）。・これらのことから反復パラメータ（反復インピーダンス、伝搬定数）を求める問題もまた固有値問題に帰着する理論の時に影像パラメータと反復パラメータが同じ物であることを直感したのだが、まんざら間違っていなかったようだ。どちらも回路そのものが生来持つ固有値と固有ベクトルで表される。線形代数の本はどれも数学者が書いたものなので数学的な厳密性や伝統（メンツ）を保っているため、手っ取り早く固有値問題だけ理解したいという工学系の輩には理解不能である。電気回路ではn次元とか一般的な問題は当座は必要なく、二次元行列の固有値問題だけで良いのだが、それだと数学的には意味が無いので講義の時に受講者の関心を引くためのネタに使うことはあってもそれを書物で扱うことはない。あっても帰納法でn=2から順番に試してnが任意の自然数でも成り立つというのを証明するぐらいである。n=2だけでとりあえず十分なんだけど、どうしてもnが任意の一般形を扱う形になってしまう。それと交流回路では複素数が基本だが数学的には複素数を扱うと実数の場合と同じではないので更に余計な拡張定理を証明していかないといけない。なので入門書の類ではページ数の制約から実数に限定したものも少なくない。実際実数だけで済む応用分野（経済とか統計、ファイナンスとか）も多いのでそれでもそこそこ本が売れる。しかし複素数を元とする場合にそれらがそのまま成り立つかというと厳密には否であるわけで。なんとも微妙なところである。それと専門的な固有値問題の本では主に代数的に解けない５次元以上の行列を扱う方法が中心的となる。５次元以上の変換行列では特性方程式の次数が５以上になるため代数的には解けない（解の公式が存在しない）ためである。従ってなんらかの反復アルゴリズムによってケースバイケースで解を求めないといけない。それをなるべく有限で短い時間で行う方法が今日まで様々なものが考案されていてその紹介に多くのページが必要となる。これも今のところ二端子対回路では要らない。なので結局自分でゼロからn=2の行列で複素数を元とする固有値問題の解法を考える必要がある。そんなのは理数系から見ると中途半端な仕事なので誰からも評価されないのは明らかで手を付けないわけだよね。工学系は必要なので各自自分で考えるしかないと。さてここから影像パラメータを固有値と固有ベクトルから導出してみよう。数学的に厳密な証明を抜きに要点だけをプロットすることにする。線形代数の本では様々なケースについて検討されているが当面今の問題を解く上で必要なもの以外はとりあえず無視する。最初に疑問に上がるのが固有値や固有ベクトルって何？という点である。これについても一応自分なりに当座納得できる解釈を図で示そう。先の問題では入力端子対条件を数ベクトルQ、出力端子対条件を数ベクトルPで表したが、元の二端子対回路とその鏡像回路の縦続接続点の端子対条件をR(E3,I3)としよう。元の二端子対回路のF行列をF,その鏡像回路のF行列をFiとするとそれらを縦続接続した回路全体のF行列はL=F.Fiとなる。これらの関係を幾何学的に図で表すと出力ベクトルPは後段の鏡像回路の変換行列FiによってRに写像され、Rは前段の二端子対回路の変換行列FによってQに写像される。一般にはPとQは変換によって異なる（互いの駆動点インピーダンスがZ01と異なる）ものになると考えられる。ところが駆動点インピーダンスが他方の端子対に接続されたZ01と等しくなるようにZ01をうまく選ぶことが出来るとすれば、この時のλ=E1/E2=I1/I2が固有値、Z01が固有ベクトルの構成要素に該当する。λとZ01はE1,I1,E2,I2の大きさによらず一意的に回路パラメータから決まることになる。交流回路ではE1,I1,E2,I2は複素数なのでZ01,λも当然ながら複素数定数となるので、実数での固有値と固有ベクトルのようにP,Qが同じ方向を持ちスケール（λ）だけ違うというようにはならないが実数だとすると図のような関係になる。複素数だと説明に苦慮する部分だ。次ぎの疑問ははたしてそういったZ01が存在するのだろうか？という点である先の固有値ー固有ベクトル方程式を変形すると $\begin{eqnarray}<br />\left(\lambda I-L x\right)&=&0,\,\,x\ne0<br />\end{eqnarray}$ を満たす非自明な解が存在しなければならないことを意味する。ここで自明な解とはx=0である。係数行列に逆行列が存在すると上の式の両辺にその逆行列を乗じると $\begin{eqnarray}<br />\left(\lambda I-L \right)^{-1}\left(\lambda I-L \right)x&=&0\\<br />x&=&0,\,\,x\ne0\\<br />\end{eqnarray}$ ということになりx=0以外の解は存在しないことになり非自明な解が存在するという前提と矛盾する。したがって非自明な解が存在するには係数行列の逆行列が存在しないことが必要条件となる。逆行列が存在しないとはどういうことか？それは線形代数の行列と行列式を学んでいればわかる通り、行列式が0となる特異行列(singular matrix)には逆行列が存在しないということである。逆行列の要素の分母は元の行列の行列式となるのでそれが0だと要素が不定となり逆行列が得られないことになる。その係数行列とその行列式は $\begin{eqnarray}<br />L&=&\left[\begin{array}A D+B C & 2 A B\\ 2 C D & A D+B C\end{array}\right]\\<br />\left(\lambda I-L\right)&=&\lambda\left[\begin{array}1&0\\0&1\end{array}\right]-\left[\begin{array}A D+B C & 2 A B\\ 2 C D & A D+B C\end{array}\right]\\<br />&=&\left[\begin{array}\lambda&0\\0&\lambda\end{array}\right]-\left[\begin{array}A D+B C & 2 A B\\ 2 C D & A D+B C\end{array}\right]\\<br />&=&\left[\begin{array}\lambda-\left(A D+B C\right)&-2 A B\\-2 C D&\lambda-\left(A D+B C\right)\end{array}\right]\\<br />\left\|\lambda I-L\right\|&=&\left( \lambda-\left(A D+B C\right)\right)^2-4 A B C D\\<br />&=&\left(\lambda-\left(A D+B C\right)+2\sqrt{A B C D}\right)\left(\lambda-\left(A D+B C\right)-2\sqrt{A B C D}\right)\\<br />&=&\left(\lambda-\left(A D+B C-2\sqrt{A B C D}\right)\right)\left(\lambda-\left(A D+B C+2\sqrt{A B C D}\right)\right)<br />&=&0<br />\end{eqnarray}$ ということになる。従って行列式の値が0（特異行列）となるλは $\begin{eqnarray}<br />\lambda_1&=&A D+B C-2\sqrt{A B C D}=\left(\sqrt{A D}-\sqrt{B C}\right)^2\\<br />\lambda_2&=&A D+B C+2\sqrt{A B C D}=\left(\sqrt{A D}+\sqrt{B C}\right)^2<br />\end{eqnarray}$ ということになる。これがこの縦続接続回路の固有値である。先の固有値ー固有ベクトル方程式でλが既知となって不定元でなくなると残る不定元xに関する斉次方程式となるので固有ベクトルxを解くことができるはずである λ1,λ2についてそれぞれ固有ベクトルxを解くと $\begin{eqnarray}<br />x&=&\left[\begin{array}1\\\frac{1}{Z_{01}}\end{array}\right]\\<br />\left(\lambda_1 I-L\right)x&=&\left[\begin{array}\lambda_1-\left(A D+B C\right)&-2 A B\\-2 C D&\lambda_1-\left(A D+B C\right)\end{array}\right]x\\<br />&=&\left[\begin{array}\cancel{A D+B C}-2\sqrt{A B C D}-\cancel{\left(A D+B C\right)}&-2 A B\\-2 C D&\cancel{A D+B C}-2\sqrt{A B C D}-\cancel{\left(A D+B C\right)}\end{array}\right]x\\<br />&=&\left[\begin{array}-2 \sqrt{A B C D} & -2 A B\\ -2 C D & -2 \sqrt{A B C D}\end{array}\right]x\\<br />&=&\left[\begin{array}-2 \sqrt{A B C D} & -2 A B\\ -2 C D & -2 \sqrt{A B C D}\end{array}\right]\left[\begin{array}1\\\frac{1}{Z_{01}}\end{array}\right]\\<br />&=&\left[\begin{array}-\frac{2 A B}{Z_{01}}-2 \sqrt{A B C D}\\ -\frac{2 \sqrt{A B C D}}{Z_{01}}-2 C D\end{array}\right]=\left[\begin{array}0\\0\end{array}\right]\\<br />Z_{01}&=&-\frac{A B}{\sqrt{A B C D}}=-\frac{\sqrt{A B C D}}{C D}=-\sqrt{\frac{A B}{C D}}<br />\end{eqnarray}$ ということになる。これは実数部が負なので線形受動回路の影像インピーダンスとしてはあり得ない。同様にλ2に対する固有ベクトルを解くと $\begin{eqnarray}<br />\left(\lambda_2 I-L\right)x&=&\left[\begin{array}\lambda_2-\left(A D+B C\right)&-2 A B\\-2 C D&\lambda_2-\left(A D+B C\right)\end{array}\right]x\\<br />&=&\left[\begin{array}\cancel{A D+B C}+2\sqrt{A B C D}-\cancel{\left(A D+B C\right)}&-2 A B\\-2 C D&\cancel{A D+B C}+2\sqrt{A B C D}-\cancel{\left(A D+B C\right)}\end{array}\right]x\\<br />&=&\left[\begin{array}2 \sqrt{A B C D} & -2 A B\\ -2 C D & 2 \sqrt{A B C D}\end{array}\right]x\\<br />&=&\left[\begin{array}2 \sqrt{A B C D} & -2 A B\\ -2 C D & 2 \sqrt{A B C D}\end{array}\right]\left[\begin{array}1\\\frac{1}{Z_{01}}\end{array}\right]\\<br />&=&\left[\begin{array}-\frac{2 A B}{Z_{01}}+2 \sqrt{A B C D}\\ \frac{2 \sqrt{A B C D}}{Z_{01}}-2 C D\end{array}\right]=\left[\begin{array}0\\0\end{array}\right]\\<br />Z_{01}&=&\frac{A B}{\sqrt{A B C D}}=\frac{\sqrt{A B C D}}{C D}=\sqrt{\frac{A B}{C D}}<br />\end{eqnarray}$ ということになり、今度は実数部が正なのでこれが影像インピーダンスの片割れということになる。同様に伝達定数θもλ2の自然対数を二分の１したものとして求めることができるのはMaximaで得た結果で既に示した通り。同様にZ02はもう片割れの縦続接続回路（変換行列の順番を入れ替えたもの）の影像インピーダンスを求めればMaximaで解いたのと同じ結果が得られる。なんとなく狐につままれた気がしないでもないが。とりあえず今日の時点ではここまでにしておこう。数学的に厳密にこれが影像パラメータと同値かどうかというのを証明していないので仕方がない。ただ固有値ー固有ベクトルとして憶えたほうが導出の見通しが良いのは確かだ。憶えておく必要があるのは「影像パラメータは固有値と固有ベクトルから成る」の一つだけだから。さてあと残るは４端子定数を影像パラメータで表すという問題。理論を学んだ時になんとか姑息な手段で導くことはできたが、もっと見通しの良い方法はないものだろうか？すでに影像パラメータを４端子定数で表した以下の関係式を得ているので、これを４端子定数に関する連立方程式として解けばよさそうに一見思える $\begin{eqnarray}<br />Z_{01}&=&\sqrt{\frac{A B}{ C D}}\\<br />Z_{02}&=&\sqrt{\frac{B D}{ A C}}\\<br />exp{\theta}&=&\sqrt{A D}+\sqrt{B C}\\<br />A D-B C&=&\left(\sqrt{A D}-\sqrt{B C}\right)\left(\sqrt{A D}+\sqrt{B C}\right)=1<br />\end{eqnarray}$ しかしこれをMaximaに与えて解かせてみると解けない。理論の時にやったようにヒューリスティックな思考錯誤方法なら解は見いだせる。しかしやってみないと解らない方法では見通しが悪すぎる。別のアプローチとして固有値ー固有ベクトル方程式を以下の様に行列展開すると $\begin{eqnarray}<br />\left(L-\lambda I\right) x&=&\left(L-exp{2\theta}I\right)x=0\\<br />\left[\begin{array}A D+B C-exp{2\theta} & 2 A B\\ 2 C D & A D+B C-exp{2\theta}\end{array}\right]\left[\begin{array}1\\\frac{1}{Z_{01}}\end{array}\right]&=&\left[\begin{array}-exp{2\theta}+\frac{2 A B}{Z_{01}}+A D+B C\\ \frac{-exp{2\theta}+A D+B C}{Z_{01}}+2 C D\end{array}\right]=0\\<br />\left[\begin{array}-exp{2\theta}+A D+B C & 2 B D\\ 2 A C & -exp{2\theta}+A D+B C\end{array}\right]\left[\begin{array}1\\\frac{1}{Z_{02}}\end{array}\right]&=&\left[\begin{array}-exp{2\theta}+\frac{2 B D}{Z_{02}}+A D+B C\\ \frac{-exp{2\theta}+A D+B C}{Z_{02}}+2 A C\end{array}\right]=0<br />\end{eqnarray}$ これらの結果から以下の連立方程式が得られる $\begin{eqnarray}<br />\left(A D+B C-exp{2\theta}\right)Z_{01}+2 A B&=&0\\<br />2 C D Z_{01}+A D+B C-exp{2\theta}&=&0\\<br />\left(A D+B C-exp{2\theta}\right)Z_{02}+2 B D&=&0\\<br />2 A C Z_{02}+A D+B C-exp{2\theta}&=&0\\<br />A D-B C&=&1<br />\end{eqnarray}$ これをMaximaに与えて解くと $\begin{eqnarray}<br />&&\left[A=-\frac{{e}^{-\theta} \left( {e}^{2 \theta}+1\right) \sqrt{Z_{01}}}{2 \sqrt{Z_{02}}},B=-\frac{{e}^{-\theta} \left( {e}^{2 \theta}-1\right) \sqrt{Z_{01}} \sqrt{Z_{02}}}{2},C=-\frac{{e}^{-\theta} \left( {e}^{2 \theta}-1\right) }{2 \sqrt{Z_{01}} \sqrt{Z_{02}}},D=-\frac{{e}^{-\theta} \left( {e}^{2 \theta}+1\right) \sqrt{\frac{Z_{02}}{Z_{01}}}}{2} \right],\\<br />&&\left[A=\frac{{e}^{-\theta} \left( {e}^{2 \theta}+1\right) \sqrt{Z_{01}}}{2 \sqrt{Z_{02}}},B=\frac{{e}^{-\theta} \left( {e}^{2 \theta}-1\right) \sqrt{Z_{01}} \sqrt{Z_{02}}}{2},C=\frac{{e}^{-\theta} \left( {e}^{2 \theta}-1\right) }{2 \sqrt{Z_{01}} \sqrt{Z_{02}}},D=\frac{{e}^{-\theta} \left( {e}^{2 \theta}+1\right) \sqrt{\frac{Z_{02}}{Z_{01}}}}{2}\right]<br />\end{eqnarray}$ という結果が得られる。Maximaではさすがに複素双曲線関数で置き換えるところまではやってくれないので、自分で整理すると $\begin{eqnarray}<br />&&\frac{{e}^{-\theta} \left( {e}^{2 \theta}+1\right)}{2}=\frac{{e}^{ \theta}+{e}^{-\theta}}{2}=\cosh(\theta)\\<br />&&\frac{{e}^{-\theta} \left( {e}^{2 \theta}-1\right)}{2}=\frac{{e}^{ \theta}-{e}^{-\theta}}{2}=\sinh(\theta)\\<br />&&\left[A=-\sqrt{\frac{Z_{01}}{Z_{02}}}\cosh(\theta),B=-\sqrt{Z_{01} Z_{02}}\sinh(\theta),C=-\frac{1}{ \sqrt{Z_{01} Z_{02}}}\sinh(\theta),D=-\sqrt{\frac{Z_{02}}{Z_{01}}}\cosh(\theta) \right],\\<br />&&\left[A=\sqrt{\frac{Z_{01}}{Z_{02}}}\cosh(\theta),B=\sqrt{Z_{01} Z_{02}}\sinh(\theta),C=\frac{1}{ \sqrt{Z_{01} Z_{02}}}\sinh(\theta),D=\sqrt{\frac{Z_{02}}{Z_{01}}}\cosh(\theta)\right]<br />\end{eqnarray}$ 線形受動回路ではB,Cの実数部は常に正でなければならないので後者が解となる。題意では影像インピーダンスを４端子定数で表すことだけ求めていたのでこれは余分だったかもしれない。 Maximaは簡単に解いてしまうが、手計算で解こうとするとA,B,C,Dに関する二次形式になるため、線形代数的にそっからどうすればいいかわからない。これは読者の課題としよう(´∀` ) P.S 実はMaximaで固有値ー固有ベクトルを求めた結果の形式と合わせるために固有ベクトルの形式を意図的に変形している。自分で計算する分にはx=matrix([Z01],[1])のままで良いのだが、Maximaはx=matrix([1],[1/Z01])の形にしてしまうようだ。固有ベクトルの標準化とか正規化のたぐいだと思われるがそれ以上詳しいことは現時点ではわからない。 P.S 片方の端子対に接続されたZ01を変化させた場合に他方の端子対から見た駆動点インピーダンスがどのように変化するのかプロットしてみたかったが、Z01は複素平面のあらゆる点を取り得るので、駆動点インピーダンスは複素平面そのものの等角写像となりRiemann面を考える必要がある。時間があったら簡単な非対称２端子対回路を例にやってみたい。どこかでZ01と駆動点インピーダンスがぴったり一致する点が現れるはずである。 P.S (1)後で良く見たら何度も登場している「回路網理論I」の反復パラメータのところで以下の通りしっかり書いてあった...orz　そうだよね。Sパラメータが先に出てきてイメージパラメータと反復パラメータをそこから導出している難しいとこだったので読み飛ばしていた。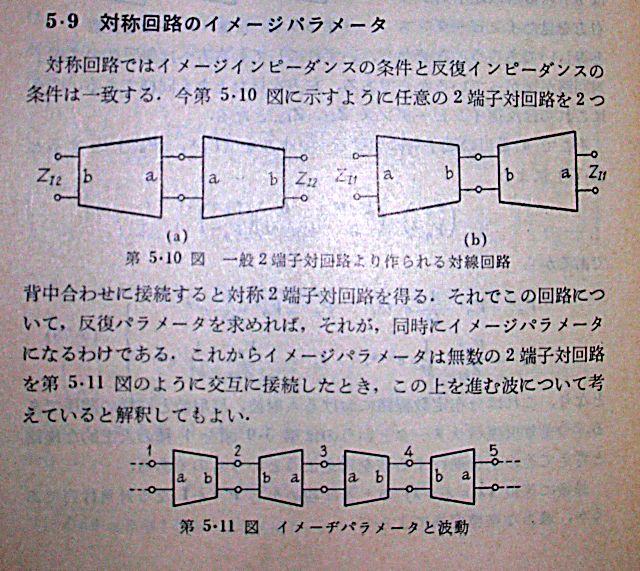これも独力で同じ着想に到達したのだから良しとしよう。 P.S その後の大学課程「電気回路(2)改訂第３版」では「回路網理論I」にあった固有値や固有ベクトルに関する記述は一切消えている。その間になにか支障があったのだろうか。確かに複素数の固有値ー固有ベクトルは実数のそれと比べて難しく直感的に捉えにくい。特に電気回路では固有ベクトルがそのまま端子対条件とはならないので更に説明がややこしくなる。

webadm	投稿日時: 2010-6-12 22:30
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3090	影像パラメータふう、前問で一週間も費やしてしまった。次ぎの問題も影像パラメータ関連。２つの異なる影像パラメータ(Z01,θ1,Z02とZ02,θ2,Z03)を持つ二端子対回路を縦続接続した場合に、全体の回路の影像パラメータがZ01,θ1+θ2,Z03となることを証明せよというもの。またこのような二端子対回路がn段縦続接続される場合はどうなるかというもの。図に描くと縦続接続された回路の４端子定数を求めてみると $\begin{eqnarray}<br />F_1&=&\left[\begin{array}\sqrt{\frac{Z_{01}}{Z_{02}}}\,\cosh(\theta_1)&\sqrt{Z_{01}Z_{02}}\,\sinh(\theta_1)\\\frac{1}{\sqrt{Z_{01}Z_{02}}}\,\sinh(\theta_1)&\sqrt{\frac{Z_{02}}{Z_{01}}}\,\cosh(\theta_1)\end{array}\right]\\<br />F_2&=&\left[\begin{array}\sqrt{\frac{Z_{02}}{Z_{03}}}\,\cosh(\theta_2)&\sqrt{Z_{02}Z_{03}}\,\sinh(\theta_2)\\\frac{1}{\sqrt{Z_{02}Z_{03}}}\,\sinh(\theta_2)&\sqrt{\frac{Z_{03}}{Z_{02}}}\,\cosh(\theta_2)\end{array}\right]\\<br />F&=&F_1 F_2\\<br />&=&\left[\begin{array}\sqrt{\frac{Z_{01}}{Z_{02}}}\cosh(\theta_1)&\sqrt{Z_{01}Z_{02}}\,\sinh(\theta_1)\\\frac{1}{\sqrt{Z_{01}Z_{02}}}\,\sinh(\theta_1)&\sqrt{\frac{Z_{02}}{Z_{01}}}\,\cosh(\theta_1)\end{array}\right]\left[\begin{array}\sqrt{\frac{Z_{02}}{Z_{03}}}\,\cosh(\theta_2)&\sqrt{Z_{02}Z_{03}}\,\sinh(\theta_2)\\\frac{1}{\sqrt{Z_{02}Z_{03}}}\,\sinh(\theta_2)&\sqrt{\frac{Z_{03}}{Z_{02}}}\,\cosh(\theta_2)\end{array}\right]\\<br />&=&\left[\begin{array}\frac{\sinh( \theta_1) \,\sinh( \theta_2) \sqrt{Z_{01} \cancel{Z_{02}}}}{\sqrt{\cancel{Z_{02}} Z_{03}}}+\cosh(\theta_1) \,\cosh(\theta_2) \sqrt{\frac{Z_{01}}{\cancel{Z_{02}}}}\sqrt{\frac{\cancel{Z_{02}}}{Z_{03}}} & \cosh( \theta_1) \,\sinh( \theta_2) \sqrt{\frac{Z_{01}}{\cancel{Z_{02}}}}\sqrt{\cancel{Z_{02}} Z_{03}}+\sinh( \theta_1) \,\cosh( \theta_2) \sqrt{Z_{01} \cancel{Z_{02}}}\sqrt{\frac{Z_{03}}{\cancel{Z_{02}}}}\\ \frac{\cosh( \theta_1) \,\sinh( \theta_2) \sqrt{\frac{\cancel{Z_{02}}}{Z_{01}}}}{\sqrt{\cancel{Z_{02}} Z_{03}}}+\frac{\sinh( \theta_1) \,\cosh( \theta_2) \sqrt{\frac{\cancel{Z_{02}}}{Z_{03}}}}{\sqrt{Z_{01} \cancel{Z_{02}}}} & \frac{\sinh( \theta_1) \,\sinh( \theta_2) \sqrt{\cancel{Z_{02}} Z_{03}}}{\sqrt{Z_{01} \cancel{Z_{02}}}}+\cosh( \theta_1) \,\cosh( \theta_2) \sqrt{\frac{\cancel{Z_{02}}}{Z_{01}}} \sqrt{\frac{Z_{03}}{\cancel{Z_{02}}}}\end{array}\right]\\<br />&=&\left[\begin{array}\frac{\cosh( \theta_1+\theta_2) \sqrt{Z_{01}}}{\sqrt{Z_{03}}} & \sinh( \theta_1+\theta_2) \sqrt{Z_{01}}\sqrt{Z_{03}}\\ \frac{\sinh( \theta_1+\theta_2) }{\sqrt{Z_{01}}\sqrt{Z_{03}}} & \frac{\cosh( \theta_1+\theta_2) \sqrt{Z_{03}}}{\sqrt{Z_{01}}}\end{array}\right]\\<br />&=&\left[\begin{array}\sqrt{\frac{Z_{01}}{Z_{03}}}\,\cosh( \theta) & \sqrt{Z_{01}Z_{03}}\,\sinh( \theta) \\ \frac{1}{\sqrt{Z_{01} Z_{03}}}\,\sinh( \theta) & \sqrt{\frac{Z_{03}}{Z_{01}}}\,\cosh( \theta) \end{array}\right]\\<br />\theta&=&\theta_1+\theta_2<br />\end{eqnarray}$ 従って影像パラメータはZ01,θ1+θ2,Z03ということになる。またn段縦続接続される場合には帰納的に $\begin{eqnarray}<br />F&=&\prod_{k=1}^{n}F_k\\<br />&=&\left[\begin{array}\sqrt{\frac{Z_{01}}{Z_{n+1}}}\,\cosh( \theta) & \sqrt{Z_{01}Z_{n+1}}\,\sinh( \theta) \\ \frac{1}{\sqrt{Z_{01} Z_{n+1}}}\,\sinh( \theta) & \sqrt{\frac{Z_{n+1}}{Z_{01}}}\,\cosh( \theta) \end{array}\right]\\<br />\theta&=&\sum_{k=1}^{n}\theta_k=\theta_1+\theta_2+\cdots+\theta_n<br />\end{eqnarray}$ となることから影像パラメータはZ01,θ1+θ2+...+θn,Zn+1ということになる。

webadm	投稿日時: 2010-6-13 5:07
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3090	続：影像パラメータ次ぎは影像パラメータの応用問題。以下の二端子対回路の影像パラメータをZ01,Z02,θとするにはZ1,Z2,Z3をどのようにすればよいか求めよというもの。まず題意を理解する必要がある。これはこれまでの問題と趣旨が違って、解析的ではなく設計的な問題である。今までは影像パラメータを予め与えられた何かで表せというものだった、これは言い換えると影像パラメータが他の何かのパラメータから一意に決まる関数だということと、その関数の式を明らかにせよというものだったが、これは影像パラメータとそれを実現する回路の形が予め指定されていて、未知数である素子の定数を決定せよというもの。設計問題は解析問題の逆問題である。これまでに影像パラメータは以下の通り４端子定数の関数として表されることを知っている $\begin{eqnarray}<br />Z_{01}&=&f_1\left(A,B,C,D\right)=\sqrt{\frac{A B}{C D}}\\<br />Z_{02}&=&f_2\left(A,B,C,D\right)=\sqrt{\frac{B D}{A C}}\\<br />\theta&=&f_3\left(A,B,C,D\right)=\ln\left(A D+B C\right)<br />\end{eqnarray}$ 今度の問題は逆にT型回路のZ1,Z2,Z3が影像パラメータの関数で表されるとしたら、それはどういった関数になるかというもの $\begin{eqnarray}<br />Z_1&=&g_1\left(Z_{01},Z_{02},\theta\right)\\<br />Z_2&=&g_2\left(Z_{01},Z_{02},\theta\right)\\<br />Z_3&=&g_3\left(Z_{01},Z_{02},\theta\right)<br />\end{eqnarray}$ 考えられる解法のアプローチとしてはZ1,Z2,Z3を不定元としたままで影像パラメータをZ1,Z2,Z3の関数として導き、連立方程式としてZ1,Z2,Z3を解くことが考えられる。 $\begin{eqnarray}<br />Z_{01}&=&h_1\left(Z_1,Z_2,Z_3\right)\\<br />Z_{02}&=&h_2\left(Z_1,Z_2,Z_3\right)\\<br />\theta&=&h_3\left(Z_1,Z_2,Z_3\right)<br />\end{eqnarray}$ しかしこれは以前の問題でも４端子定数で表された影像パラメータの式から逆に４端子定数を影像パラメータで表す式を導出する際でも試みたが方程式は得られるがそれを解くのは人間がやっても容易ではないし、ましてやMaximaでは解けないことが判っている。本当かどうかは実際にやって確かめてみればよい。従ってこのアプローチは早々に捨てて別のアプローチを探る必要がある。既に４端子定数が以下の通り影像パラメータの関数として表されることを知っている $\begin{eqnarray}<br />A&=&u_1\left(Z_{01},Z_{02},\theta\right)=\sqrt{\frac{Z_{01}}{Z_{02}}}\,\cosh(\theta)\\<br />B&=&u_2\left(Z_{01},Z_{02},\theta\right)=\sqrt{Z_{01}Z_{02}}\,\sinh(\theta)\\<br />C&=&u_3\left(Z_{01},Z_{02},\theta\right)=\frac{1}{\sqrt{Z_{01}Z_{02}}}\,\sinh(\theta)\\<br />D&=&u_4\left(Z_{01},Z_{02},\theta\right)=\sqrt{\frac{Z_{02}}{Z_{01}}}\,\cosh(\theta)<br />\end{eqnarray}$ ならばZ1,Z2,Z3が４端子定数の関数として表すことができれば、それは影像パラメータの関数でもあることになる $\begin{eqnarray}<br />Z_1&=&v_1\left(A,B,C,D\right)=v_1\left(u_1,u_2,u_3,u_4\right)=g_1\left(Z_{01},Z_{02},\theta\right)\\<br />Z_2&=&v_2\left(A,B,C,D\right)=v_2\left(u_1,u_2,u_3,u_4\right)=g_2\left(Z_{01},Z_{02},\theta\right)\\<br />Z_3&=&v_3\left(A,B,C,D\right)=v_3\left(u_1,u_2,u_3,u_4\right)=g_3\left(Z_{01},Z_{02},\theta\right)<br />\end{eqnarray}$ u1,u2,u3,u4は既知なので、v1,v2,v3がわかればA,B,C,Dをu1,u2,u3,u4で置き換えたものがg1,g2,g3ということになる。長々となったが、著者の解も基本的には同じアプローチをとっている。著者はオーソドックスな代数操作で結果を得ているが、こちらはそれとは違う線形代数的手法でやってみよう。さてここで足踏み状態。オーソドックスな式の代入とか操作なら著者の解と何一つ変わらないので意味が無い。理論の時に試みようとしたが壁にぶち当たってしまった。同じ課題に直面している。どうしても元の回路にアドミッタンス要素があるので有理式が出てきてしまう。それをインピーダンスに直すと今度は不定元の二次式になってしまう。二次形式を使わないと行列では表現することができない。二次形式をどう扱えばよいかは勉強していないので解らない。歴史的には線形代数よりも二次形式の方がずっと古い。古くはDiophantusに始まり、彼の著書にインスパイアされたFermatによって重要な課題がいくつも見いだされ、以後Eulerや多くの数学者がその課題に挑んできた。GaussによればLagrangeが既に多くの発見をしており、その後を継いだのがLegendreだが近代数学に至る道を切り開いたのがGaussであった。Gauss以前の数学者は個々の特殊な問題に対する興味深い発見を提供したが、一般化を目指すものではなく発展性もなかった。それら散在する発見をひとまとめに包含しそれを超える一般論を構築したのがGaussの天才性である。Gaussはそれを２０代で成し遂げて著作にしたのだが、その時代には行列も行列式も代数理論も無かったもののGauss自身は生来の天才性で近代に通用する代数的概念を常識的に利用していた。後生になってDirichletがGaussの著書を常に携帯し急発展してきた代数理論と照らし合わせて解釈するという偉業を成し遂げた。Dirichletはそれを講義でしか公開しなかったので、後にDedekindがそれらを著書にまとめた。Gaussの著書"Disquisitiones Arithmeticae"(略してD.A.と呼ばれる、日本語訳では"ガウス整数論"として知られる）数学史上の遺産だがそれを近代的な代数理論で再構成し平易化したDirichlet-Dedekindの"Vorlesungen uber Zahlentheoric"(日本語訳本"ディレクレデデキント整数論講義")は代数的数論論のバイブルである。実のところこの問題はそういった数学の血脈につながるものがあるのだが、そうした方向に目を向かせると電気回路理論の本道ではなく脇道にそれ近代数学の世界にワープしかねないブラックホールが潜んでいるので、絶対にそのブラックホールに近づかないように安易な解法を教えてしまうことにしているように見える。こっから先は闇だと言うと若い人は好んでそっちへ行こうとするので、その道の存在自体を教えなければ良いのである。そもそも電気回路を代数的に扱おうとする時点で、こうした近代数学理論へつながるブラックホール（境界領域）はいたるところに潜んでいる運命にある。残念ながら大学ではそんな脇道にそれていたら満足に卒業できないので時間の都合上脇目をそらせないように教える必要があるわけである。しかし独学だとそういった結界は無いので、境界領域のその先を覗き見することは自由である。二次形式はそんなわけで、歴史的には線形代数よりも遙かに歴史は古いが固有値問題よりも後にならないと教えられない。しばらく二次形式について勉強してくる(;´Д`) ふう、二次形式を調べているつもりだったけど、とっくに通り過ぎて代数幾何やグロブナー基底の世界やら非線形方程式や無理方程式を眺めてた、最近の学校はエクセルで方程式の解法を教えるのね。結局自分の納得の行くやり方は見つからず。自分でゼロから考えるしかないという結論に。最初からやってみると、まず問題の回路の４端子定数を導いてみよう。Z1,Z2,Z3それぞれひとつだけから成る部分回路の従属接続として計算することができる。 $\begin{eqnarray}<br />F_1&=&\left[\begin{array}1&Z_1\\0&1\end{array}\right]\\<br />F_2&=&\left[\begin{array}1&0\\\frac{1}{Z_2}&1\end{array}\right]<br />F_3&=&\left[\begin{array}1&Z_3\\0&1\end{array}\right]\\<br />F&=&F_1 F_2 F_3\\<br />&=&\left[\begin{array}1&Z_1\\0&1\end{array}\right]\left[\begin{array}1&0\\\frac{1}{Z_2}&1\end{array}\right]\left[\begin{array}1&Z_3\\0&1\end{array}\right]\\<br />&=&\left[\begin{array}\frac{Z_1}{Z_2}+1 & Z_1\,\left( \frac{Z_3}{Z_2}+1\right) +Z_3\\ \frac{1}{Z_2} & \frac{Z_3}{Z_2}+1\end{array}\right]\\<br />&=&\left[\begin{array}\frac{Z_2+Z_1}{Z_2} & \frac{Z_2\,Z_3+Z_1\,Z_3+Z_1\,Z_2}{Z_2}\\ \frac{1}{Z_2} & \frac{Z_3+Z_2}{Z_2}\end{array}\right]\\<br />&=&\left[\begin{array}A&B\\C&D\end{array}\right]<br />\end{eqnarray}$ この結果から逆にZ1,Z2,Z3を解こうとしてもMaximaでは解けない。中学生で習う代入法を使えばC=1/Z2からZ2=1/Cが、それをAの式に代入してA=1+CZ1からZ1=(A-1)/Cが導かれそれらをBかDの式に代入すれば残りのZ3が導かれる。それがMaximaでは出来ないというのがsolveで実装されているアルゴリズムの守備範囲で無いということだろうか。しかし代入法以外に解法はないのかという納得がいかない疑問が残る。連立方程式に二次と一次の項が混じっているのが原因かもしれない。二次の項だけなら過去さらりと解いているし。それで二次形式を勉強している間に重要な事に気づいた。二次の項が伴うだけで既に線形ではないということである。また二次の項のみなら二次形式で表されるが、一次の項が混じるとそうはいかない。それに早い時点で気づくべきだった...orz 二次形式は二次同次多項式のみを対象とするのに対して、二次曲面は二次方程式一般を対象とするため、そちらを勉強すべきだった。実は二次曲面を扱っている線形代数の本もある。既に線形ではないのにどういうことだろう。実は一般的な二次方程式は適当な座標軸をうまくとると二次形式で表される。それによって得られる二次形式はいくつかの種類のどれかになる。一般の二次方程式の二次の項は二次形式で以下の様に行列表記される $x^{t}A x&=&\begin{eqnarray}<br />\left[\begin{array}x_1.x_2,\cdots,x_n\end{array}\right]\left[\begin{array}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{array}\right]\left[\begin{array}x_1\\x_2\\\vdots\\x_n\end{array}\right]<br />\end{eqnarray}$ 残る一次の項は $\begin{eqnarray}<br />2 b x&=&2\left[\begin{array}b_1,b_2,\cdots,b_n\end{array}\right]\left[\begin{array}x_1\\x_2\\\vdots\\x_n\end{array}\right]<br />\end{eqnarray}$ 従ってn元の二次方程式は一般に $\begin{eqnarray}<br />x^{t}A x+2 b x+c&=&\left[\begin{array}x_1.x_2,\cdots,x_n\end{array}\right]\left[\begin{array}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{array}\right]\left[\begin{array}x_1\\x_2\\\vdots\\x_n\end{array}\right]+2\left[\begin{array}b_1,b_2,\cdots,b_n\end{array}\right]\left[\begin{array}x_1\\x_2\\\vdots\\x_n\end{array}\right]+c\\<br />&=&0<br />\end{eqnarray}$ と行列表記することができる。ここでxがx'から座標軸の回転と並行移動を施したものとすると $\begin{eqnarray}<br />x&=&P x^{\'}+x_0\\<br />x^{t}A x+2 b x+c&=&\left(P x^{\'}+x_0\right)^{t}A \left(P x^{\'}+x_0\right)+2 b \left(P x^{\'}+x_0\right)+c\\<br />&=&\left(P x^{\'}\right)^{t}A P x^{\'}+{x_0}^{t}A P x^{\'}+\left(P x^{\'}\right)^{t}A x_0+2 b P x^{\'}+{x_0}^{t} A x_0+2 b x_0+c\\<br />&=&x^{\'}^{t}P^{t}A P x^{\'}+{x_0}^{t}A P x^{\'}+x^{\'}^{t}P^{t}A x_0+2 b P x^{\'}+{x_0}^{t} A x_0+2 b x_0+c\\<br />&=&x^{\'}^{t}A^{\'}x^{\'}+2b^{\'}x^{\'}+c^{\'}\\<br />&=&0\\<br />A^{\'}&=&P^{t}A P\\<br />b^{\'}&=&\left({x_0}^{t}A+b\right) P\\<br />c^{\'}&=&\left({x_0}^{t} A+2 b\right) x_0+c<br />\end{eqnarray}$ と書き換えることができる。ここで以下が成り立つように並行移動量x0を適切に選ぶと $\begin{eqnarray}<br />{x_0}^{t}A+b&=&0\\<br />{x_0}^{t}A&=&-b<br />\end{eqnarray}$ b'=0となるので $\begin{eqnarray}<br />x^{\'}^{t}A^{\'}x^{\'}+c^{\'}&=&0<br />\end{eqnarray}$ という標準形となり二次形式論とつながる。二次曲面は二次元の場合、線形変換Aと回転Pと並行移動x0によって１点、円、楕円、双曲線、２直線、１直線、放物線、空集合のいずれかをとる。３次元の場合には同様にして楕円面、一様双曲面、二葉双曲面、推面、楕円放物線、双曲放物線、楕円柱面、双曲柱面、交差２平面、放物柱面、並行２平面、１平面、１直線、１点のいずれかになる。従って先の連立方程式の解はそれぞれの方程式が与えるすべての二次曲面が交わる点の集合である。実際に３次元と行っても複素数なので普段見慣れている三次元空間の曲面とは厳密には同じではないが、数式上では同じように扱うことができる。歴史的には二次形式論がずっと古く線形代数や代数幾何は戦後に後から構築されたのだが構造的には新しい順から学んだ方が体系的には見通しが良くなる。しかし歴史的な経緯で戦前や戦後の線形代数も代数幾何もまだなかった頃の二次形式論が長い間教えられてきた関係で上記の二次曲面（二次曲線）論と二次形式論の講義の順番はまちまちである。さてこっからどうすんだ(;´Д`) ふと思い立ってA,B,Cに関する連立方程式のみMaximaに与えたらあっさり解けた...orz $\begin{verbatim}<br />solve([e1,e2,e3],[Z1,Z2,Z3]);<br />\end{verbatim}\\<br />\left[\left[Z_1=\frac{A-1}{C},Z_2=\frac{1}{C},Z_3=\frac{B\,C-A+1}{A\,C}\right]\right]$ Maximaはいったいどうやって解いているんだろ。確かにA,B,C,Dは一次独立ではないので行列Rank=3で３つが決まれば十分なのだけれども。上記のA,B,Cにそれぞれ影像パラメータ表記を代入すると $\begin{eqnarray}<br />Z_1&=&\frac{A-1}{C}=\frac{\sqrt{\frac{Z_{01}}{\cancel{Z_{02}}}}\,\cosh(\theta)-1}{\frac{1}{\sqrt{Z_{01}\cancel{Z_{02}}}}\,\sinh(\theta)}=Z_{01}\coth(\theta)-\sqrt{Z_{01}Z_{02}}\,cosech(\theta)\\<br />Z_2&=&\frac{1}{C}=\frac{1}{\frac{1}{\sqrt{Z_{01}Z_{02}}}\,\sinh(\theta)}=\sqrt{Z_{01}Z_{02}}\,cosech(\theta)\\<br />Z_3&=&\frac{B\,C-A+1}{A\,C}=\frac{\sqrt{\cancel{Z_{01}Z_{02}}}\,\sinh(\theta)\,\frac{1}{\sqrt{\cancel{Z_{01}Z_{02}}}}\,\sinh(\theta)-\sqrt{\frac{Z_{01}}{Z_{02}}}\,\cosh(\theta)+1}{\sqrt{\frac{\cancel{Z_{01}}}{Z_{02}}}\,\cosh(\theta)\,\frac{1}{\sqrt{\cancel{Z_{01}}Z_{02}}}\,\sinh(\theta)}=Z_{02}\,\coth(\theta)-\sqrt{Z_{01}Z_{02}}\,cosech(\theta)<br />\end{eqnarray}$ ということになり著者と同じ結果が得られる。これでよしとしよう。

webadm	投稿日時: 2010-6-17 5:13
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3090	続々：影像パラメータ次ぎは影像パラメータを求める問題。以下の２つのL型回路の伝送行列と影像パラメータを求めよというもの。著者のとは違う方法で求めてみよう。ストラテジーとしては伝送行列を２つの部分回路の縦続接続として導いた後、その鏡像回路と縦続接続した対称回路の伝送行列の固有値と固有ベクトルとして影像パラメータを導く。左端の回路の伝送行列F1は $\begin{eqnarray}<br />F_1&=&\left[\begin{array}1&0\\\frac{1}{Z_1}&1\end{array}\right]\left[\begin{array}1&Z_2\\0&1\end{array}\right]\\<br />&=&\left[\begin{array}1 & Z_2\\ \frac{1}{Z_1} & \frac{Z_2+Z_1}{Z_1}\end{array}\right]<br />\end{eqnarray}$ 次ぎに鏡像回路との従属接続した対称回路の固有値と固有ベクトルとして影像パラメータを求めると $\begin{eqnarray}<br />A_{01}&=&F_1 F_{i1}=\left[\begin{array}1 & Z_2\\ \frac{1}{Z_1} & \frac{Z_2+Z_1}{Z_1}\end{array}\right]\left[\begin{array}\frac{Z_2+Z_1}{Z_1} & Z_2\\ \frac{1}{Z_1} & 1\end{array}\right]\\<br />&=&\left[\begin{array}\frac{2\,Z_2+Z_1}{Z_1} & 2\,Z_2\\ \frac{2\,\left( Z_2+Z_1\right) }{{Z_1}^{2}} & \frac{2\,Z_2+Z_1}{Z_1}\end{array}\right]\\<br />\left\|\lambda I-A_{01}\right\|&=&\left\|\begin{array}\lambda-\frac{2\,Z_2+Z_1}{Z_1} & -2\,Z_2\\ -\frac{2\,\left( Z_2+Z_1\right) }{{Z_1}^{2}} & \lambda-\frac{2\,Z_2+Z_1}{Z_1}\end{array}\right\|\\<br />&=&{\left( \lambda-\frac{2\,Z_2+Z_1}{Z_1}\right) }^{2}-\frac{4\,Z_2\,\left( Z_2+Z_1\right) }{{Z_1}^{2}}\\<br />&=&\left(\lambda-\frac{2\,Z_2+Z_1}{Z_1}+\sqrt{\frac{4\,Z_2\,\left( Z_2+Z_1\right) }{{Z_1}^{2}}}\right)\left(\lambda-\frac{2\,Z_2+Z_1}{Z_1}-\sqrt{\frac{4\,Z_2\,\left( Z_2+Z_1\right) }{{Z_1}^{2}}}\right)\\<br />&=&\left(\lambda-\left(\frac{2\,Z_2+Z_1-2\sqrt{\,Z_2\,\left( Z_2+Z_1\right)}}{Z_1}\right)\right)\left(\lambda-\left(\frac{2\,Z_2+Z_1+2\sqrt{\,Z_2\,\left( Z_2+Z_1\right) }}{Z_1}\right)\right)\\<br />\lambda&=&\frac{2\,Z_2+Z_1\pm 2\sqrt{\,Z_2\,\left( Z_2+Z_1\right)}}{Z_1}\\<br />\left[\begin{array}\lambda-\frac{2\,Z_2+Z_1}{Z_1} & -2\,Z_2\\ -\frac{2\,\left( Z_2+Z_1\right) }{{Z_1}^{2}} & \lambda-\frac{2\,Z_2+Z_1}{Z_1}\end{array}\right]x&=&\left[\begin{array}\frac{\cancel{2\,Z_2+Z_1}\pm 2\sqrt{\,Z_2\,\left( Z_2+Z_1\right)}}{Z_1}-\frac{\cancel{2\,Z_2+Z_1}}{Z_1} & -2\,Z_2\\ -\frac{2\,\left( Z_2+Z_1\right) }{{Z_1}^{2}} & \frac{\cancel{2\,Z_2+Z_1}\pm 2\sqrt{\,Z_2\,\left( Z_2+Z_1\right)}}{Z_1}-\frac{\cancel{2\,Z_2+Z_1}}{Z_1}\end{array}\right]x\\<br />&=&\left[\begin{array}\pm\frac{2\sqrt{\,Z_2\,\left( Z_2+Z_1\right)}}{Z_1} & -2\,Z_2\\ -\frac{2\,\left( Z_2+Z_1\right) }{{Z_1}^{2}} & \pm\frac{2\sqrt{\,Z_2\,\left( Z_2+Z_1\right)}}{Z_1}\end{array}\right]\left[\begin{array}Z_{01}\\1\end{array}\right]\\<br />&=&\left[\begin{array}\pm Z_{01}\frac{2\sqrt{\,Z_2\,\left( Z_2+Z_1\right)}}{Z_1}-2\,Z_2\\\pm Z_{01}\frac{2\,\left( Z_2+Z_1\right) }{{Z_1}^{2}}-\frac{2\sqrt{\,Z_2\,\left( Z_2+Z_1\right)}}{Z_1}\end{array}\right]=\left[\begin{array}0\\0\end{array}\right]\\<br />Z_{01}&=&\frac{Z_1\,Z_2}{\sqrt{Z_2\,\left( Z_2+Z_1\right) }}\\<br />&=&Z_1\sqrt{\frac{Z_2}{Z_2+Z_1}}\\<br />\end{eqnarray}$ $\begin{eqnarray}<br />A_{02}&=& F_{i1} F_1=\left[\begin{array}\frac{Z_2+Z_1}{Z_1} & Z_2\\ \frac{1}{Z_1} & 1\end{array}\right]\left[\begin{array}1 & Z_2\\ \frac{1}{Z_1} & \frac{Z_2+Z_1}{Z_1}\end{array}\right]\\<br />&=&\left[\begin{array}\frac{2\,Z_2+Z_1}{Z_1} & \frac{2\,Z_2\,\left( Z_2+Z_1\right) }{Z_1}\\ \frac{2}{Z_1} & \frac{2\,Z_2+Z_1}{Z_1}\end{array}\right]\\<br />\left[\begin{array}\lambda-\frac{2\,Z_2+Z_1}{Z_1} & -\frac{2\,Z_2\,\left( Z_2+Z_1\right) }{Z_1}\\ -\frac{2}{Z_1} & \lambda-\frac{2\,Z_2+Z_1}{Z_1}\end{array}\right]x&=&\left[\begin{array}\frac{\cancel{2\,Z_2+Z_1}\pm 2\sqrt{\,Z_2\,\left( Z_2+Z_1\right)}}{Z_1}-\frac{\cancel{2\,Z_2+Z_1}}{Z_1} & -\frac{2\,Z_2\,\left( Z_2+Z_1\right) }{Z_1}\\ -\frac{2}{Z_1} & \frac{\cancel{2\,Z_2+Z_1}\pm 2\sqrt{\,Z_2\,\left( Z_2+Z_1\right)}}{Z_1}-\frac{\cancel{2\,Z_2+Z_1}}{Z_1}\end{array}\right]x\\<br />&=&\left[\begin{array}\pm\frac{2\sqrt{\,Z_2\,\left( Z_2+Z_1\right)}}{Z_1} & -\frac{2\,Z_2\,\left( Z_2+Z_1\right) }{Z_1}\\ -\frac{2}{Z_1} & \pm\frac{2\sqrt{\,Z_2\,\left( Z_2+Z_1\right)}}{Z_1}\end{array}\right]\left[\begin{array}Z_{02}\\1\end{array}\right]\\<br />&=&\left[\begin{array}\pm Z_{02}\frac{2\sqrt{\,Z_2\,\left( Z_2+Z_1\right)}}{Z_1}-\frac{2\,Z_2\,\left( Z_2+Z_1\right) }{Z_1}\\\pm Z_{02}\frac{2}{Z_1}-\frac{2\sqrt{\,Z_2\,\left( Z_2+Z_1\right)}}{Z_1}\end{array}\right]=\left[\begin{array}0\\0\end{array}\right]\\<br />Z_{02}&=&\sqrt{Z_2\,\left( Z_2+Z_1\right) }\\<br />\end{eqnarray}$ $\begin{eqnarray}<br />2\theta&=&\ln\left(\lambda\right)=\ln\left(\frac{2\,Z_2+Z_1+ 2\sqrt{\,Z_2\,\left( Z_2+Z_1\right)}}{Z_1}\right)\\<br />&=&\ln\left(2\sqrt{\frac{ Z_2}{Z_1}}\sqrt{\frac{ Z_2}{Z_1}+1}+\frac{2 Z_2}{Z_1}+ 1\right)\\<br />&=&\ln\left(\sqrt{\frac{Z_2}{Z_1}}+\sqrt{\frac{Z_2}{Z_1}+1}\right)^2\\<br />&=&2\ln\left(\sqrt{\frac{Z_2}{Z_1}}+\sqrt{\frac{Z_2}{Z_1}+1}\right)\\<br />\theta&=&\ln\left(\sqrt{\frac{Z_2}{Z_1}}+\sqrt{\frac{Z_2}{Z_1}+1}\right)\\<br />exp{\theta}&=&\sqrt{\frac{Z_2}{Z_1}}+\sqrt{\frac{Z_2}{Z_1}+1}\\<br />exp{-\theta}&=&\frac{1}{\sqrt{\frac{Z_2}{Z_1}}+\sqrt{\frac{Z_2}{Z_1}+1}}=\frac{\sqrt{Z_1}}{\sqrt{Z_2+Z_1}+\sqrt{Z_2}}\\<br />\cosh(\theta)&=&\frac{exp{\theta}+exp{-\theta}}{2}=\frac{\sqrt{\frac{Z_2}{Z_1}}+\sqrt{\frac{Z_2}{Z_1}+1}+\frac{\sqrt{Z_1}}{\sqrt{Z_2+Z_1}+\sqrt{Z_2}}}{2}=\frac{\left( \sqrt{Z_2}\,\sqrt{Z_2+Z_1}+Z_2+Z_1\right) }{\sqrt{Z_1}\,\left( \sqrt{Z_2+Z_1}+\sqrt{Z_2}\right)}=\frac{\sqrt{Z_2+Z_1}\left( \cancel{\sqrt{Z_2}+\sqrt{Z_2+Z_1}}\right) }{\sqrt{Z_1}\,\left( \cancel{\sqrt{Z_2+Z_1}+\sqrt{Z_2}}\right)}\\<br />&=&\sqrt{\frac{Z_2}{Z_1}+1}\\<br />\theta&=&\cosh^{-1}(\sqrt{\frac{Z_2}{Z_1}+1})<br />\end{eqnarray}$ ということになる。一方右端の回路の伝送行列は $\begin{eqnarray}<br />F_2&=&\left[\begin{array}1&\frac{Z_1}{2}\\0&1\end{array}\right]\left[\begin{array}1&0\\\frac{1}{2 Z_2}&1\end{array}\right]\\<br />&=&\left[\begin{array}\frac{Z_1}{4\,Z_2}+1 & \frac{Z_1}{2}\\ \frac{1}{2\,Z_2} & 1\end{array}\right]<br />\end{eqnarray}$ 従って影像パラメータは $\begin{eqnarray}<br />B_{01}&=&F_2 F_{i2} =\left[\begin{array}\frac{Z_1}{4\,Z_2}+1 & \frac{Z_1}{2}\\ \frac{1}{2\,Z_2} & 1\end{array}\right]\left[\begin{array}1 & \frac{Z_1}{2}\\ \frac{1}{2\,Z_2} & \frac{Z_1}{4\,Z_2}+1\end{array}\right]\\<br />&=&\left[\begin{array}\frac{2\,Z_2+Z_1}{2\,Z_2} & \frac{Z_1\,\left( 4\,Z_2+Z_1\right) }{4\,Z_2}\\ \frac{1}{Z_2} & \frac{2\,Z_2+Z_1}{2\,Z_2}\end{array}\right]\\<br />\left\|\lambda I-B_{01}\right\|&=&\left\|\begin{array}\lambda-\frac{2\,Z_2+Z_1}{2\,Z_2} & -\frac{Z_1\,\left( 4\,Z_2+Z_1\right) }{4\,Z_2}\\ -\frac{1}{Z_2} & \lambda-\frac{2\,Z_2+Z_1}{2\,Z_2}\end{array}\right\|\\<br />&=&{\left( \lambda-\frac{2\,Z_2+Z_1}{2\,Z_2}\right) }^{2}-\frac{Z_1\,\left( 4\,Z_2+Z_1\right) }{4\,{Z_2}^{2}}\\<br />&=&\left(\lambda-\left(\frac{2\,Z_2+Z_1}{2\,Z_2}-\sqrt{\frac{Z_1\,\left( 4\,Z_2+Z_1\right) }{4\,{Z_2}^{2}}}\right)\right)\left(\lambda-\left(\frac{2\,Z_2+Z_1}{2\,Z_2}+sqrt{\frac{Z_1\,\left( 4\,Z_2+Z_1\right) }{4\,{Z_2}^{2}}}\right)\right)\\<br />&=&\left(\lambda-\left(\frac{2\,Z_2+Z_1-\sqrt{Z_1\,\left( 4\,Z_2+Z_1\right) }}{2\,Z_2}\right)\right)\left(\lambda-\left(\frac{2\,Z_2+Z_1+\sqrt{Z_1\,\left( 4\,Z_2+Z_1\right) }}{2\,Z_2}\right)\right)\\<br />\lambda&=&\frac{2\,Z_2+Z_1\pm\sqrt{Z_1\,\left( 4\,Z_2+Z_1\right) }}{2\,Z_2}\\<br />\left[\begin{array}\lambda-\frac{2\,Z_2+Z_1}{2\,Z_2} & -\frac{Z_1\,\left( 4\,Z_2+Z_1\right) }{4\,Z_2}\\ -\frac{1}{Z_2} & \lambda-\frac{2\,Z_2+Z_1}{2\,Z_2}\end{array}\right]x&=&\left[\begin{array}\frac{\cancel{2\,Z_2+Z_1}\pm\sqrt{Z_1\,\left( 4\,Z_2+Z_1\right) }}{2\,Z_2}-\frac{\cancel{2\,Z_2+Z_1}}{2\,Z_2} & -\frac{Z_1\,\left( 4\,Z_2+Z_1\right) }{4\,Z_2}\\ -\frac{1}{Z_2} & \frac{\cancel{2\,Z_2+Z_1}\pm\sqrt{Z_1\,\left( 4\,Z_2+Z_1\right) }}{2\,Z_2}-\frac{\cancel{2\,Z_2+Z_1}}{2\,Z_2}\end{array}\right]x\\<br />&=&\left[\begin{array}\frac{\pm\sqrt{Z_1\,\left( 4\,Z_2+Z_1\right) }}{2\,Z_2} & -\frac{Z_1\,\left( 4\,Z_2+Z_1\right) }{4\,Z_2}\\ -\frac{1}{Z_2} & \frac{\pm\sqrt{Z_1\,\left( 4\,Z_2+Z_1\right) }}{2\,Z_2}\end{array}\right]\left[\begin{array}Z_{01}\\1\end{array}\right]\\<br />&=&\left[\begin{array}\frac{\pm Z_{01}\sqrt{Z_1\,\left( 4\,Z_2+Z_1\right) }}{2\,Z_2}-\frac{Z_1\,\left( 4\,Z_2+Z_1\right) }{4\,Z_2}\\ -Z_{01}\frac{1}{Z_2}+\frac{\pm\sqrt{Z_1\,\left( 4\,Z_2+Z_1\right) }}{2\,Z_2}\end{array}\right]=\left[\begin{array}0\\0\end{array}\right]\\<br />Z_{01}&=&\sqrt{Z_1 Z_2+\frac{{Z_1}^2}{4}}\\<br />\end{eqnarray}$ $\begin{eqnarray}<br />B_{02}&=&F_{i2} F_2 =\left[\begin{array}1 & Z_2\\ \frac{1}{Z_1} & \frac{Z_2+Z_1}{Z_1}\end{array}\right]\left[\begin{array}\frac{Z_2+Z_1}{Z_1} & Z_2\\ \frac{1}{Z_1} & 1\end{array}\right]\\<br />&=&\left[\begin{array}\frac{2\,Z_2+Z_1}{2\,Z_2} & Z_1\\ \frac{4\,Z_2+Z_1}{4\,{Z_2}^{2}} & \frac{2\,Z_2+Z_1}{2\,Z_2}\end{array}\right]\\<br />\left[\begin{array}\lambda-\frac{2\,Z_2+Z_1}{2\,Z_2} & -Z_1\\ -\frac{4\,Z_2+Z_1}{4\,{Z_2}^{2}} & \lambda-\frac{2\,Z_2+Z_1}{2\,Z_2}\end{array}\right]x&=&\left[\begin{array}\frac{\cancel{2\,Z_2+Z_1}\pm\sqrt{Z_1\,\left( 4\,Z_2+Z_1\right) }}{2\,Z_2}-\cancel{\frac{2\,Z_2+Z_1}{2\,Z_2}} & -Z_1\\ -\frac{4\,Z_2+Z_1}{4\,{Z_2}^{2}} & \frac{\cancel{2\,Z_2+Z_1}\pm\sqrt{Z_1\,\left( 4\,Z_2+Z_1\right) }}{2\,Z_2}-\cancel{\frac{2\,Z_2+Z_1}{2\,Z_2}}\end{array}\right]x\\<br />&=&\left[\begin{array}\frac{\pm\sqrt{Z_1\,\left( 4\,Z_2+Z_1\right) }}{2\,Z_2} & -Z_1\\ -\frac{4\,Z_2+Z_1}{4\,{Z_2}^{2}} & \frac{\pm\sqrt{Z_1\,\left( 4\,Z_2+Z_1\right) }}{2\,Z_2}\end{array}\right]\left[\begin{array}Z_{02}\\1\end{array}\right]\\<br />&=&\left[\begin{array}\frac{\pm Z_{02}\sqrt{Z_1\,\left( 4\,Z_2+Z_1\right) }}{2\,Z_2}-Z_1\\ -Z_{02}\frac{4\,Z_2+Z_1}{4\,{Z_2}^{2}}+\frac{\pm\sqrt{Z_1\,\left( 4\,Z_2+Z_1\right) }}{2\,Z_2}\end{array}\right]=\left[\begin{array}0\\0\end{array}\right]\\<br />Z_{02}&=&2 Z_2\sqrt{\frac{Z_1}{Z_1+4 Z_2}}\\<br />\end{eqnarray}$ $\begin{eqnarray}<br />2\theta&=&\ln\left(\lambda\right)=\ln\left(\frac{2\,Z_2+Z_1+\sqrt{Z_1\,\left( 4\,Z_2+Z_1\right) }}{2\,Z_2}\right)\\<br />&=&\ln\left(\sqrt{\frac{Z_1}{4 Z_2}}\sqrt{\frac{Z_1}{4 Z_2}+1}+\frac{Z_1}{2 Z_2}+1\right)\\<br />&=&\ln\left(\sqrt{\frac{Z_1}{4 Z_2}}+\sqrt{\frac{Z_1}{4 Z_2}+1}\right)^2\\<br />&=&2\ln\left(\sqrt{\frac{Z_1}{4 Z_2}}+\sqrt{\frac{Z_1}{4 Z_2}+1}\right)\\<br />\theta&=&\ln\left(\sqrt{\frac{Z_1}{4 Z_2}}+\sqrt{\frac{Z_1}{4 Z_2}+1}\right)\\<br />exp{\theta}&=&\sqrt{\frac{Z_1}{4 Z_2}}+\sqrt{\frac{Z_1}{4 Z_2}+1}\\<br />exp{-\theta}&=&\frac{1}{\sqrt{\frac{Z_1}{4 Z_2}}+\sqrt{\frac{Z_1}{4 Z_2}+1}}=\frac{2\,Z_2}{\sqrt{Z_1\,\left( 4\,Z_2+Z_1\right) }+2\,Z_2+Z_1}\\<br />\cosh(\theta)&=&\frac{exp{\theta}+exp{-\theta}}{2}=\frac{\sqrt{\frac{Z_1}{4 Z_2}}+\sqrt{\frac{Z_1}{4 Z_2}+1}+\frac{2\,Z_2}{\sqrt{Z_1\,\left( 4\,Z_2+Z_1\right) }+2\,Z_2+Z_1}}{2}=\frac{\sqrt{Z_1}\,\sqrt{4\,Z_2+Z_1}+4\,Z_2+Z_1}{2\,\sqrt{Z_2}\,\left( \sqrt{4\,Z_2+Z_1}+\sqrt{Z_1}\right) }=\frac{\,\sqrt{4\,Z_2+Z_1}\left(\cancel{\sqrt{Z_1}+\sqrt{4\,Z_2+Z_1}}\right)}{2\,\sqrt{Z_2}\,\left( \cancel{\sqrt{4\,Z_2+Z_1}+\sqrt{Z_1}}\right) }\\<br />&=&\sqrt{\frac{Z_1}{4 Z_2}+1}\\<br />\theta&=&\cosh^{-1}(\sqrt{\frac{Z_1}{4 Z_2}+1})<br />\end{eqnarray}$ ということになる。 P.S 二つ目の回路で対称回路の伝送行列が間違っていて期待と違う計算結果しかでなくだいぶ悩んだのは内緒だ。転記した際に間違えたのかもしれないが、幸いもう片方の対称回路で固有値と固有ベクトルをMaximaで計算をやり直したら期待した結果がでたので間違いだとわかった。計算結果があっているかどうかは、(1)固有値を固有値ー固有ベクトル方程式に代入してみて行列式の値がゼロになるかどうか確認する。(2)４端子パラメータの影像パラメータ表現式に得られた影像パラメータを代入し元の４端子パラメータと一致するか検算することで確認できる。面倒でパズル的な固有値の素因子分解は最初自分でやったが、後半はMaximaを使用した便利である。 $\begin{verbatim}<br />solve([2ab=sqrt(Z1(4Z2+Z1))/(2Z2),a^2+b^2=(2Z2+Z1)/(2*Z2)],[a,b]);<br />\end{verbatim}\\<br />\left[\left[a=-\frac{\sqrt{\frac{Z_1}{Z_2}+4}}{2},b=-\frac{\sqrt{Z_1}}{2\,\sqrt{Z_2}}],[a=\frac{\sqrt{\frac{Z_1}{Z2}+4}}{2},b=\frac{\sqrt{Z_1}}{2\,\sqrt{Z_2}}],[a=-\frac{\sqrt{\frac{Z_1}{Z_2}}}{2},b=-\frac{\sqrt{4\,Z_2+Z_1}}{2\,\sqrt{Z_2}}],[a=\frac{\sqrt{\frac{Z_1}{Z_2}}}{2},b=\frac{\sqrt{4\,Z_2+Z_1}}{2\,\sqrt{Z_2}}\right]\right]<br />$

webadm	投稿日時: 2010-6-17 16:21
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3090	影像インピーダンス次ぎは影像インピーダンスの理解を試す問題。以下の回路で端子対1-1'から見た駆動点インピーダンスがZ01に等しく、端子対2-2'から見た駆動点インピーダンスがZ02に等しくなるようにするにはZ01,Z02をどのように選べば良いか導けというもの。影像インピーダンスの問題だと気づかないと大変難しい問題となる。問題文には一言も影像インピーダンスとは書いていないので用語と公式一夜漬けだと落とす問題。実務でもそういわれれば知っているが、言われるまでそうとは気が付かないということがよくある。影像インピーダンスを導く問題だとわかれば簡単だが、そうとわからないようにしているところがひっかけ問題である。著者の解答は記憶力優秀で公式を正確に記憶して思い出せる場合の解答である。しかし人は思い出した時には既に記憶があやふやだということが少なくない。Z01=sqrt(AB/CD)だったかな、いやAC/BDだったかもしれないとか、いろいろ組み合わせがあったのを思い出してしまってどれがどれだか混乱してしまう。大抵そういうときは間違った記憶に基づいて計算して出来たつもりになってしまう。計算自体は式が間違っていても結果は出るからね。ここではずぼらな一夜漬けもせず暗記もしない、もしくは一夜漬けはしたけど肝心の公式を忘れてしまったという場合の解法をやってみよう。公式を忘れても固有値問題のことを忘れていなければ問題ない。最初に二端子対回路としての伝送行列をもとめると３つの部分回路に分けてその縦続接続とすれば $\begin{eqnarray}<br />F_1&=&\left[\begin{array}1&Z_1\\0&1\end{array}\right]\\<br />F_2&=&\left[\begin{array}1&0\\\frac{1}{Z_2}&1\end{array}\right]\\<br />F_3&=&\left[\begin{array}1&Z_3\\0&1\end{array}\right]\\<br />F&=&F_1 F_2 F_3=\left[\begin{array}1&Z_1\\0&1\end{array}\right]\left[\begin{array}1&0\\\frac{1}{Z_2}&1\end{array}\right]\left[\begin{array}1&Z_3\\0&1\end{array}\right]\\<br />&=&\left[\begin{array}\frac{Z_2+Z_1}{Z_2} & \frac{Z_2\,Z_3+Z_1\,Z_3+Z_1\,Z_2}{Z_2}\\ \frac{1}{Z_2} & \frac{Z_3+Z_2}{Z_2}\end{array}\right]<br />\end{eqnarray}$ 次ぎに端子対2-2'に鏡を置いて端子対1-1'から眺めたような対称回路の伝送行列を求めてその固有ベクトルとして影像インピーダンスZ01を求める。 $\begin{eqnarray}<br />A_{01}&=&F F_i=\left[\begin{array}\frac{Z_2+Z_1}{Z_2} & \frac{Z_2\,Z_3+Z_1\,Z_3+Z_1\,Z_2}{Z_2}\\ \frac{1}{Z_2} & \frac{Z_3+Z_2}{Z_2}\end{array}\right]\left[\begin{array}\frac{Z_3+Z_2}{Z_2} & \frac{Z_2\,Z_3+Z_1\,Z_3+Z_1\,Z_2}{Z_2}\\ \frac{1}{Z_2} & \frac{Z_2+Z_1}{Z_2}\end{array}\right]\\<br />&=&\left[\begin{array}\frac{2 Z_2 Z_3+2 Z_1 Z_3+{Z_2}^{2}+2 Z_1 Z_2}{{Z_2}^{2}} & \frac{2 \left( Z_2+Z_1\right) \,\left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right) }{{Z_2}^{2}}\\ \frac{2\,\left( Z_3+Z_2\right) }{{Z_2}^{2}} & \frac{2 Z_2 Z_3+2 Z_1 Z_3+{Z_2}^{2}+2 Z_1 Z_2}{{Z_2}^{2}}\end{array}\right]\\<br />\left\|\lambda I-A_{01}\right\|&=&\left\|\begin{array}\lambda-\frac{2 Z_2 Z_3+2 Z_1 Z_3+{Z_2}^{2}+2 Z_1 Z_2}{{Z_2}^{2}} & -\frac{2 \left( Z_2+Z_1\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right) }{{Z_2}^{2}}\\ -\frac{2 \left( Z_3+Z_2\right) }{{Z_2}^{2}} & \lambda-\frac{2 Z_2 Z_3+2 Z_1 Z_3+{Z_2}^{2}+2 Z_1 Z_2}{{Z_2}^{2}}\end{array}\right\|\\<br />&=&{\left( \lambda-\frac{2 Z_2 Z_3+2 Z_1 Z_3+{Z_2}^{2}+2 Z_1 Z_2}{{Z_2}^{2}}\right) }^{2}-\frac{4 \left( Z_2+Z_1\right) \left( Z_3+Z_2\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right) }{{Z_2}^{4}}\\<br />&=&\left(\lambda-\left(\frac{2 Z_2 Z_3+2 Z_1 Z_3+{Z_2}^{2}+2 Z_1 Z_2-2\sqrt{\left( Z_2+Z_1\right) \left( Z_3+Z_2\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right)}}{{Z_2}^{2}}\right)\right)\left(\lambda-\left(\frac{2 Z_2 Z_3+2 Z_1 Z_3+{Z_2}^{2}+2 Z_1 Z_2+2\sqrt{\left( Z_2+Z_1\right) \left( Z_3+Z_2\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right)}}{{Z_2}^{2}}\right)\right)\\<br />\lambda&=&\frac{2 Z_2 Z_3+2 Z_1 Z_3+{Z_2}^{2}+2 Z_1 Z_2\pm 2\sqrt{\left( Z_2+Z_1\right) \left( Z_3+Z_2\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right)}}{{Z_2}^{2}}\\<br />&&\left[\begin{array}\lambda-\frac{2 Z_2 Z_3+2 Z_1 Z_3+{Z_2}^{2}+2 Z_1 Z_2}{{Z_2}^{2}} & -\frac{2 \left( Z_2+Z_1\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right) }{{Z_2}^{2}}\\ -\frac{2 \left( Z_3+Z_2\right) }{{Z_2}^{2}} & \lambda-\frac{2 Z_2 Z_3+2 Z_1 Z_3+{Z_2}^{2}+2 Z_1 Z_2}{{Z_2}^{2}}\end{array}\right]x\\<br />&=&\left[\begin{array}\frac{\cancel{2 Z_2 Z_3+2 Z_1 Z_3+{Z_2}^{2}+2 Z_1 Z_2}\pm 2\sqrt{\left( Z_2+Z_1\right) \left( Z_3+Z_2\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right)}}{{Z_2}^{2}}-\cancel{\frac{2 Z_2 Z_3+2 Z_1 Z_3+{Z_2}^{2}+2 Z_1 Z_2}{{Z_2}^{2}}} & -\frac{2 \left( Z_2+Z_1\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right) }{{Z_2}^{2}}\\ -\frac{2 \left( Z_3+Z_2\right) }{{Z_2}^{2}} & \frac{\cancel{2 Z_2 Z_3+2 Z_1 Z_3+{Z_2}^{2}+2 Z_1 Z_2}\pm 2\sqrt{\left( Z_2+Z_1\right) \left( Z_3+Z_2\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right)}}{{Z_2}^{2}}-\cancel{\frac{2 Z_2 Z_3+2 Z_1 Z_3+{Z_2}^{2}+2 Z_1 Z_2}{{Z_2}^{2}}}\end{array}\right]x\\<br />&=&\left[\begin{array}\frac{\pm 2\sqrt{\left( Z_2+Z_1\right) \left( Z_3+Z_2\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right)}}{{Z_2}^{2}} & -\frac{2 \left( Z_2+Z_1\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right) }{{Z_2}^{2}}\\ -\frac{2 \left( Z_3+Z_2\right) }{{Z_2}^{2}} & \frac{\pm 2\sqrt{\left( Z_2+Z_1\right) \left( Z_3+Z_2\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right)}}{{Z_2}^{2}}\end{array}\right]\left[\begin{array}Z_{01}\\1\end{array}\right]\\<br />&=&\left[\begin{array}\frac{\pm 2Z_{01}\sqrt{\left( Z_2+Z_1\right) \left( Z_3+Z_2\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right)}}{{Z_2}^{2}}-\frac{2 \left( Z_2+Z_1\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right) }{{Z_2}^{2}}\\ -Z_{01}\frac{2 \left( Z_3+Z_2\right) }{{Z_2}^{2}}+\frac{\pm 2\sqrt{\left( Z_2+Z_1\right) \left( Z_3+Z_2\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right)}}{{Z_2}^{2}}\end{array}\right]=\left[\begin{array}0\\0\end{array}\right]\\<br />Z_{01}&=&\sqrt{\frac{\left( Z_2+Z_1\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right)}{ Z_3+Z_2}}<br />\end{eqnarray}$ 同様に反対向きも $\begin{eqnarray}<br />A_{02}&=&F_i F =\left[\begin{array}\frac{Z_3+Z_2}{Z_2} & \frac{Z_2\,Z_3+Z_1\,Z_3+Z_1\,Z_2}{Z_2}\\ \frac{1}{Z_2} & \frac{Z_2+Z_1}{Z_2}\end{array}\right]\left[\begin{array}\frac{Z_2+Z_1}{Z_2} & \frac{Z_2\,Z_3+Z_1\,Z_3+Z_1\,Z_2}{Z_2}\\ \frac{1}{Z_2} & \frac{Z_3+Z_2}{Z_2}\end{array}\right]\\<br />&=&\left[\begin{array}\frac{2 Z_2 Z_3+2 Z_1 Z_3+{Z_2}^{2}+2 Z_1 Z_2}{{Z_2}^{2}} & \frac{2 \left( Z_3+Z_2\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right) }{{Z_2}^{2}}\\ \frac{2 \left( Z_2+Z_1\right) }{{Z_2}^{2}} & \frac{2 Z_2 Z_3+2 Z_1 Z_3+{Z_2}^{2}+2 Z_1 Z_2}{{Z_2}^{2}}\end{array}\right]\\<br />&&\left[\begin{array}\lambda-\frac{2 Z_2 Z_3+2 Z_1 Z_3+{Z_2}^{2}+2 Z_1 Z_2}{{Z_2}^{2}} & -\frac{2 \left( Z_3+Z_2\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right) }{{Z_2}^{2}}\\ -\frac{2 \left( Z_2+Z_1\right) }{{Z_2}^{2}} & \lambda-\frac{2 Z_2 Z_3+2 Z_1 Z_3+{Z_2}^{2}+2 Z_1 Z_2}{{Z_2}^{2}}\end{array}\right]x\\<br />&=&\left[\begin{array}\frac{\cancel{2 Z_2 Z_3+2 Z_1 Z_3+{Z_2}^{2}+2 Z_1 Z_2}\pm 2\sqrt{\left( Z_2+Z_1\right) \left( Z_3+Z_2\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right)}}{{Z_2}^{2}}-\cancel{\frac{2 Z_2 Z_3+2 Z_1 Z_3+{Z_2}^{2}+2 Z_1 Z_2}{{Z_2}^{2}}} & -\frac{2 \left( Z_3+Z_2\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right) }{{Z_2}^{2}}\\ -\frac{2 \left( Z_2+Z_1\right) }{{Z_2}^{2}} & \frac{\cancel{2 Z_2 Z_3+2 Z_1 Z_3+{Z_2}^{2}+2 Z_1 Z_2}\pm 2\sqrt{\left( Z_2+Z_1\right) \left( Z_3+Z_2\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right)}}{{Z_2}^{2}}-\cancel{\frac{2 Z_2 Z_3+2 Z_1 Z_3+{Z_2}^{2}+2 Z_1 Z_2}{{Z_2}^{2}}}\end{array}\right]x\\<br />&=&\left[\begin{array}\frac{\pm 2\sqrt{\left( Z_2+Z_1\right) \left( Z_3+Z_2\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right)}}{{Z_2}^{2}} & -\frac{2 \left( Z_3+Z_2\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right) }{{Z_2}^{2}}\\ -\frac{2 \left( Z_2+Z_1\right) }{{Z_2}^{2}} & \frac{\pm 2\sqrt{\left( Z_2+Z_1\right) \left( Z_3+Z_2\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right)}}{{Z_2}^{2}}\end{array}\right]\left[\begin{array}Z_{02}\\1\end{array}\right]\\<br />&=&\left[\begin{array}\frac{\pm 2 Z_{02}\sqrt{\left( Z_2+Z_1\right) \left( Z_3+Z_2\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right)}}{{Z_2}^{2}}-\frac{2 \left( Z_3+Z_2\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right) }{{Z_2}^{2}}\\ -Z_{02}\frac{2 \left( Z_2+Z_1\right) }{{Z_2}^{2}}+\frac{\pm 2\sqrt{\left( Z_2+Z_1\right) \left( Z_3+Z_2\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right)}}{{Z_2}^{2}}\end{array}\right]=\left[\begin{array}0\\0\end{array}\right]\\<br />Z_{02}&=&\sqrt{\frac{\left( Z_2+Z_3\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right)}{ Z_1+Z_2}}<br />\end{eqnarray}$ ということになる。ところで既に賢明な読者は２つの対称回路で違うのはZ1とZ3の位置だけだということにお気づきだろう。Z02は計算せずともZ01の式のZ1とZ3をスワップすれば良い。元の回路が対称回路の場合にはZ1=Z3であることから $\begin{eqnarray}<br />Z_{01}&=&\sqrt{\frac{\left( Z_2+Z_1\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right)}{ Z_3+Z_2}}\\<br />&=&\sqrt{\frac{\cancel{\left( Z_2+Z_1\right)} \left( Z_2 Z_1+Z_1 Z_1+Z_1 Z_2\right)}{ \cancel{Z_1+Z_2}}}\\<br />&=&\sqrt{Z_1\left( 2 Z_2+Z_1\right)}\\<br />Z_{02}&=&\sqrt{\frac{\left( Z_2+Z_3\right) \left( Z_2 Z_3+Z_1 Z_3+Z_1 Z_2\right)}{ Z_1+Z_2}}\\<br />&=&\sqrt{\frac{\cancel{\left( Z_2+Z_1\right)} \left( Z_2 Z_1+Z_1 Z_1+Z_1 Z_2\right)}{ \cancel{Z_1+Z_2}}}\\<br />&=&\sqrt{Z_1\left( 2 Z_2+Z_1\right)}\\<br />&=&Z_{01}<br />\end{eqnarray}$ ということになる。 P.S 前問と同じだという思われるかもしれない。その通りだ。馬鹿の一つ覚えというやつである。（ﾟεﾟ）ｷﾆｼﾅｲ!!（ﾟεﾟ）ｷﾆｼﾅｲ!!

webadm	投稿日時: 2010-6-17 19:40
Webmaster 登録日: 2004-11-7 居住地: 投稿: 3090	続：影像インピーダンス次ぎも影像インピーダンスを求める問題。以下の回路の左端及び右端から見た影像インピーダンスを求めよというもの著者は計算を少なくするために予め工夫している興味深い方法を示している。昔は計算は計算尺か対数表（吐血）を使って人間がやるしかないので時間的にも労力的にもコストが高かった。なので計算量はなるべく減らした方が良いという考えが支配的だった。Gaussは計算好きというか、計算を理論的に改良する趣味を持っていた。無理数を小数点以下できるだけ長く計算するために少ない労力で正確に短時間に済む方法を考えていたので、計算など弟子にやらせればと言われると憤慨したという。電気回路でもこれまでの問題で見てきたようにたかがT型回路を２つ縦続接続するだけで固有値問題を解くのに大変な数式のボリュームになる。Maximaのような数式処理ソフトが傍らにあるのでなんとか扱えるが、それ無しでやるとなると転記ミスやらなにやらで手に負えないかもしれない。なので闇雲に計算に頼らずにもっと易しい別解があればそちらを見つけた方がトータルでは良い結果になるかもしれない。実務では特許とかいろいろのしがらみがあって既知の解法は使えないため多少劣った方法でも別解を使わざるを得ない場合がある。ソフトウェアでは特に物理的な見た目とか使い勝手は特許になっている可能性があるので、そのまま真似するのは禁物である。ましてや他人のコードを事前の承諾なく流用することなども。必要であれば同じことをするコードを新たにゼロから書き下ろすということも必要になる。クリーンルーム開発というやつである。ベトナムとかソフトウェア開発コストが日本の一割（関税を除く）で済むところにそうしたクリーンルーム開発を委託すれば、オリジナルのコードが少ない予算で手にいれることができる。ゼロから書くなら誰がやっても同じだから格安なとこに頼めばよいと考えるからである。しかし裏でそれがどっかに流れて似たようなものが他社でもっと短時間で開発されるというリスクはある。誰も監視できないしね。日本の大手ソフトハウスが国内で受注して開発したはずの防衛関係のソフトのソースコードを偶然関係者が眺めたら、誰も読まない中国語のコメントの中に中国人民軍所有と書いてあったとか、なかったとか。なんの話しだったっけ。影像インピーダンスの話しだった。出題者の意図は闇雲に時間と手間をかけて計算させることではない。二端子対回路と影像インピーダンスについて良く学んでいれば、対称回路の影像インピーダンスは両端で対称となることを知っているはずであるとふんでいる。そうすると非対称な部分だけに注意を払えばよいことになる。そうしたベストアンサーを知りたい人は著者の解法を読んでもらうとして。ここでは別解で著者と同じ結果になるか、著者の解は正しいのかを検証することにしよう。ここではまずへそ曲がりな発想として、問題のラダー回路を構成する部分回路に着目しよう。各部分回路はそれぞれどんな影像パラメータを持つのだろうか。そしてそれらが縦続接続した場合にどう変わるのか。これについてはどんな電気回路理論の本も扱っていない。対称二端子対回路の伝送行列から固有値と固有ベクトルを求めることができる。非対称回路の場合にはその鏡像回路と前後２通りの組み合わせた縦続接続回路としての対称回路の固有値と固有ベクトルとして２つの異なる影像インピーダンスを求めることができる。まず回路中に繰り返し現れる直列インピーダンスだけの部分回路はそれ自身で対称二端子対回路を構成する。伝送行列から固有値と固有ベクトル求めると $\begin{eqnarray}<br />A&=&\left[\begin{array}1&Z\\0&1\end{array}\right]\\<br />\left\|\lambda I-A\right\|&=&\left\|\begin{array}\lambda-1&-Z\\0&\lambda-1\end{array}\right\|\\<br />&=&\left(\lambda-1\right)^2\\<br />\lambda&=&1\\<br />&&\left[\begin{array}\lambda-1&-Z\\0&\lambda-1\end{array}\right]x\\<br />&=&\left[\begin{array}\cancel{1}-\cancel{1}&-Z\\0&\cancel{1}-\cancel{1}\end{array}\right]x\\<br />&=&\left[\begin{array}0&-Z\\0&0\end{array}\right]\left[\begin{array}Z_{01}\\1\end{array}\right]\\<br />&=&\left[\begin{array}-Z\\0\end{array}\right]=\left[\begin{array}0\\0\end{array}\right]\\<br />\end{eqnarray}$ なんと固有ベクトルが一意的に定まらない。強いてあるとすれば無限大のインピーダンスということになる。一方の端子対を開放した場合、他方から見た駆動点インピーダンスが無限大のインピーダンス（開放）と等しくなるからである。もう一方のアドミッタンスのみから成る部分回路についてもやってみよう $\begin{eqnarray}<br />A&=&\left[\begin{array}1&0\\\frac{1}{Z}&1\end{array}\right]\\<br />\left\|\lambda I-A\right\|&=&\left\|\begin{array}\lambda-1&0\\-\frac{1}{Z}&\lambda-1\end{array}\right\|\\<br />&=&\left(\lambda-1\right)^2\\<br />\lambda&=&1\\<br />&&\left[\begin{array}\lambda-1&0\\-\frac{1}{Z}&\lambda-1\end{array}\right]x\\<br />&=&\left[\begin{array}\cancel{1}-\cancel{1}&0\\-\frac{1}{Z}&\cancel{1}-\cancel{1}\end{array}\right]x\\<br />&=&\left[\begin{array}0&0\\-\frac{1}{Z}&0\end{array}\right]\left[\begin{array}Z_{01}\\1\end{array}\right]\\<br />&=&\left[\begin{array}0\\-\frac{Z_{01}}{Z}\end{array}\right]=\left[\begin{array}0\\0\end{array}\right]<br />\end{eqnarray}$ これも同じような感じ。強いて言えばゼロのインピーダンス（短絡）しかない。一方の端子対を短絡すると他方の端子対から見た駆動点インピーダンスがゼロ（短絡）と等しくなる。実はこれ線形代数で言う固有値が重複度2を持つケースに該当する。またこれらの行列は三角行列の格好の実例である。これらは線形代数の本で必ず出てくるがいまいち実感が湧かないでいたが、こうして目前の問題として提示されると良く調べてみようという気が起きてくる。三角行列の固有値は上記の通りいずれも対角要素そのものとなる。という当たり前のことしか大抵の線形代数の本には書いていない。これは固有ベクトルの自由度に関係するらしいがそこまで詳しく解説している本は数少ない。また重複度2の固有値に関して一つしか固有ベクトルが得られない三角行列は対角化（スペクトル分解）できないらしいが、それに触れている本も限られる。とどのつまりこれらのケースは固有値問題が解けないのではなはだ都合が悪いので華麗にスルーする必要があったわけである。こうしたケースがあるので影像パラメータと固有値問題を関連付けることはされなくなったと思われる。三角行列そのものの都合の良い性質（固有値が一目瞭然、一般の行列は上下２つの三角行列の積に分解できる）は線形代数の応用で随所に登場する。とりあえず先へ進もう。伝達インピーダンスのみ、もしくは伝達アドミッタンスのみの回路の影像パラメータは上記のような感じだが。その二つを縦続接続した場合にはどうなるのだろう？２つの相異なる対称回路を縦続接続した場合には非対称回路となる。従ってその影像パラメータを求めるには更に鏡像回路と縦続接続した伝送行列の固有値と固有ベクトルを求める必要がある。 $\begin{eqnarray}<br />A_1&=&\left[\begin{array}1&Z_1\\0&1\end{array}\right]\\<br />A_2&=&\left[\begin{array}1&0\\\frac{1}{Z_2}&1\end{array}\right]\\<br />A&=&A_1 A_2=\left[\begin{array}1&Z_1\\0&1\end{array}\right]\left[\begin{array}1&0\\\frac{1}{Z_2}&1\end{array}\right]\\<br />&=&\left[\begin{array}\frac{Z_1}{Z_2}+1 & Z_1\\ \frac{1}{Z_2} & 1\end{array}\right]\\<br />F&=&A A_i=\left[\begin{array}\frac{Z_1}{Z_2}+1 & Z_1\\ \frac{1}{Z_2} & 1\end{array}\right]\left[\begin{array}1 & Z_1\\ \frac{1}{Z_2} & \frac{Z_1}{Z_2}+1\end{array}\right]\\<br />&=&\left[\begin{array}\frac{Z_2+2 Z_1}{Z_2} & \frac{2 Z_1 \left( Z_2+Z_1\right) }{Z_2}\\ \frac{2}{Z_2} & \frac{Z_2+2 Z_1}{Z_2}\end{array}\right]\\<br />\left\|\lambda I-F\right\|&=&\left\|\begin{array}\lambda-\frac{Z_2+2 Z_1}{Z_2} & -\frac{2 Z_1 \left( Z_2+Z_1\right) }{Z_2}\\ -\frac{2}{Z_2} & \lambda-\frac{Z_2+2 Z_1}{Z_2}\end{array}\right\|\\<br />&=&{\left( \lambda-\frac{Z_2+2 Z_1}{Z_2}\right) }^{2}-\frac{4 Z_1 \left( Z_2+Z_1\right) }{{Z_2}^{2}}\\<br />&=&\left(\lambda-\frac{Z_2+2 Z_1}{Z_2}+\sqrt{\frac{4 Z_1 \left( Z_2+Z_1\right) }{{Z_2}^{2}}}\right)\left(\lambda-\frac{Z_2+2 Z_1}{Z_2}-\sqrt{\frac{4 Z_1 \left( Z_2+Z_1\right) }{{Z_2}^{2}}}\right)\\<br />&=&\left(\lambda-\left(\frac{Z_2+2 Z_1-2\sqrt{Z_1 \left( Z_2+Z_1\right) }}{Z_2}\right)\right)\left(\lambda-\left(\frac{Z_2+2 Z_1+2\sqrt{Z_1 \left( Z_2+Z_1\right) }}{Z_2}\right)\right)\\<br />\lambda&=&\frac{Z_2+2 Z_1\pm 2\sqrt{Z_1 \left( Z_2+Z_1\right) }}{Z_2}\\<br />&&\left[\begin{array}\lambda-\frac{Z_2+2 Z_1}{Z_2} & -\frac{2 Z_1 \left( Z_2+Z_1\right) }{Z_2}\\ -\frac{2}{Z_2} & \lambda-\frac{Z_2+2 Z_1}{Z_2}\end{array}\right]x\\<br />&=&\left[\begin{array}\frac{\cancel{Z_2+2 Z_1}\pm 2\sqrt{Z_1 \left( Z_2+Z_1\right) }}{Z_2}-\cancel{\frac{Z_2+2 Z_1}{Z_2}} & -\frac{2 Z_1 \left( Z_2+Z_1\right) }{Z_2}\\ -\frac{2}{Z_2} & \frac{\cancel{Z_2+2 Z_1}\pm 2\sqrt{Z_1 \left( Z_2+Z_1\right) }}{Z_2}-\cancel{\frac{Z_2+2 Z_1}{Z_2}}\end{array}\right]x\\<br />&=&\left[\begin{array}\frac{\pm 2\sqrt{Z_1 \left( Z_2+Z_1\right) }}{Z_2} & -\frac{2 Z_1 \left( Z_2+Z_1\right) }{Z_2}\\ -\frac{2}{Z_2} & \frac{\pm 2\sqrt{Z_1 \left( Z_2+Z_1\right) }}{Z_2}\end{array}\right]\left[\begin{array}Z_{01}\\1\end{array}\right]\\<br />&=&\left[\begin{array}\frac{\pm 2Z_{01}\sqrt{Z_1 \left( Z_2+Z_1\right) }}{Z_2}-\frac{2 Z_1 \left( Z_2+Z_1\right) }{Z_2}\\ -Z_{01}\frac{2}{Z_2}+\frac{\pm 2\sqrt{Z_1 \left( Z_2+Z_1\right) }}{Z_2}\end{array}\right]=\left[\begin{array}0\\0\end{array}\right]\\<br />Z_{01}&=&\sqrt{Z_1\left(Z_2+Z_1\right)}<br />\end{eqnarray}$ やっと意味のある影像インピーダンスになる。もう片方についても同様に求めると $\begin{eqnarray}<br />F^{\'}&=&A_i A=\left[\begin{array}1 & Z_1\\ \frac{1}{Z_2} & \frac{Z_1}{Z_2}+1\end{array}\right]\left[\begin{array}\frac{Z_1}{Z_2}+1 & Z_1\\ \frac{1}{Z_2} & 1\end{array}\right]\\<br />&=&\left[\begin{array}\frac{Z_2+2 Z_1}{Z_2} & 2 Z_1\\ \frac{2 \left( Z_2+Z_1\right) }{{Z_2}^{2}} & \frac{Z_2+2 Z_1}{Z_2}\end{array}\right]\\<br />&&\left[\begin{array}\lambda-\frac{Z_2+2 Z_1}{Z_2} & -2 Z_1\\ -\frac{2 \left( Z_2+Z_1\right) }{{Z_2}^{2}} & \lambda-\frac{Z_2+2 Z_1}{Z_2}\end{array}\right]x\\<br />&=&\left[\begin{array}\frac{\cancel{Z_2+2 Z_1}\pm 2\sqrt{Z_1 \left( Z_2+Z_1\right) }}{Z_2}-\cancel{\frac{Z_2+2 Z_1}{Z_2}} & -2 Z_1\\ -\frac{2 \left( Z_2+Z_1\right) }{{Z_2}^{2}} & \frac{\cancel{Z_2+2 Z_1}\pm 2\sqrt{Z_1 \left( Z_2+Z_1\right) }}{Z_2}-\cancel{\frac{Z_2+2 Z_1}{Z_2}}\end{array}\right]x\\<br />&=&\left[\begin{array}\frac{\pm 2\sqrt{Z_1 \left( Z_2+Z_1\right) }}{Z_2} & -2 Z_1\\ -\frac{2 \left( Z_2+Z_1\right) }{{Z_2}^{2}} & \frac{\pm 2\sqrt{Z_1 \left( Z_2+Z_1\right) }}{Z_2}\end{array}\right]\left[\begin{array}Z_{02}\\1\end{array}\right]\\<br />&=&\left[\begin{array}\frac{\pm 2Z_{02}\sqrt{Z_1 \left( Z_2+Z_1\right) }}{Z_2}-2 Z_1\\ -Z_{02}\frac{2 \left( Z_2+Z_1\right) }{{Z_2}^{2}}+\frac{\pm 2\sqrt{Z_1 \left( Z_2+Z_1\right) }}{Z_2}\end{array}\right]=\left[\begin{array}0\\0\end{array}\right]\\<br />Z_{02}&=&Z_2\sqrt{\frac{Z_1}{Z_2+Z_1}}<br />\end{eqnarray}$ 問題の回路を良く見ると、上記の非対称回路とその鏡像回路の複数の縦続接続であることに気づく。さてこの回路とその鏡像回路の縦続接続の伝送行列の固有ベクトルを求めればよいのだが、行列の積が多いので大変な式のボリュームになりそうである。なんとか線形代数的に固有ベクトルが簡単に導けるようにならないものかのう。直感的にはわかるのだが。それでは納得が行かない。なんかもうすっかり線形代数の応用問題みたいになってしまった。どうすんだこれ（；´Д｀）。とりあえず問題の回路は以下の様にL型回路の伝送行列とその鏡像回路の伝送行列が交互に縦続接続されたものと考えられる。そうすると全体の伝送行列は $\begin{eqnarray}<br />G&=&A A_i A A_i A=F F A\\<br />&=&F^2 A<br />\end{eqnarray}$ と表すことができる。またこれは非対称回路なのでそのまた鏡像回路と縦続接続した対称回路は $begin{eqnarray}<br />H&=&G G_i=F^2 A A_i F^2\\<br />&=&F^5<br />\end{eqnarray}$ ということになる。同様に逆向きに縦続接続したもうひとつの対称回路の場合には $\begin{eqnarray}<br />H^{\'}&=&G_i G={F^{\'}}^2 A_i A {F^{\'}}^2={F^{\'}}^2 F^{\'} {F^{\'}}^2\\<br />&=&{F^{\'}}^5<br />\end{eqnarray}$ ということになる。いずれもFかF'の５乗という対称形になる。従って問題は行列のべき乗から成る行列の固有値と固有ベクトルは元の行列のそれとどういう関係が成り立つかといいう点である。どうやらこの問いは線形代数では伝統的に自分で解き明かすべき（自ら追体験すべき）お約束の演習問題らしい。 youtubeで見たMITのLinear Algebra講義の中でこの演習問題を明瞭快活に扱っている。受講者がその場で問題を解く追体験が出来るように自然に誘導されていく。ここではべき乗に限らずより一般的化した命題として解いてみよう。これは「ラング線形代数（下）」に出てくる演習問題である。線形変換行列Aとしてλをその固有値、xを固有ベクトルとした場合、 $\begin{eqnarray}<br />A x&=&\lambda x<br />\end{eqnarray}$ が成り立つものとする。ここでfが多項式の場合、 $\begin{eqnarray}<br />f\left(A\right)x&=&f\left(\lambda\right)x<br />\end{eqnarray}$ が成り立つというもの。これを証明すればよい。 fが多項式であるということは命題の式は $\begin{eqnarray}<br />f\left(A\right)x&=&\left(c_0+c_1 A+c_2 A^2+\cdots+c_n A^n\right)x\\<br />&=&c_0 x+c_1 A x+c_2 A^2 x+\cdots+c_n A^n x<br />\end{eqnarray}$ ということになる。また固有値方程式からAのべき乗に関して帰納的に $\begin{eqnarray}<br />A^2 x&=&\lambda A x=\lambda \lambda x={\lambda}^2 x\\<br />A^n x&=&{\lambda}^n x<br />\end{eqnarray}$ が成り立つことから、これを多項式に代入すると $\begin{eqnarray}<br />f\left(A\right)x&=&c_0 x+c_1 A x+c_2 A^2 x+\cdots+c_n A^n x\\<br />&=&c_0 x + c_1 \lambda x +c_2 {\lambda}^2 x+\cdots+c_n {\lambda}^n x\\<br />&=&f\left(\lambda\right)x<br />\end{eqnarray}$ ということになる。従ってfとして単にべき乗が与えられた場合、固有値は元の行列のべき乗になるのに対して、固有ベクトルはそのまま変わらないことになる。このことから問題の回路の影像インピーダンスはわざわざ回路全体の伝送行列から求めずとも以下の関係から、基本対称回路の伝送行列の固有値と変わらないことが証明された。 $\begin{eqnarray}<br />F x&=&\lambda x\\<br />F^5 x&=&{\lambda}^5 x\\<br />F^{\'} y&=&\lambda^{\'} y\\<br />{F^{\'}}^5 y&=&{\lambda^{\'}}^5 y<br />\end{eqnarray}$ 従って影像インピーダンスは既に導いてある式から $\begin{eqnarray}<br />Z_{01}&=&\sqrt{Z_1\left(Z_2+Z_1\right)}\\<br />&=&\sqrt{j\omega L\left(\frac{1}{j\omega C}+j\omega L\right)}\\<br />&=&\sqrt{L\left(\frac{1}{C}-{\omega}^2 L\right)}\\<br />&=&\sqrt{\frac{L\left(1-{\omega}^2 L C\right)}{C}}<br />Z_{02}&=&Z_2\sqrt{\frac{Z_1}{Z_2+Z_1}}\\<br />&=&\frac{1}{j\omega C}\sqrt{\frac{j\omega L}{\frac{1}{j\omega C}+j\omega L}}\\<br />&=&\sqrt{\left(\frac{1}{j\omega C}\right)^2 \frac{j\omega L}{\frac{1}{j\omega C}+j\omega L}}\\<br />&=&\sqrt{\frac{L}{C\left(1-{\omega}^2 L C\right)}}<br />\end{eqnarray}$ ということになる。ふう、すっきりした(´∀` ) P.S 対称行列を複数縦続接続した場合にその固有ベクトルが変わらないのは最初に考察した伝達インピーダンスのみの二端子対回路や伝達アドミッタンスのみの二端子対回路の伝送行列の固有ベクトルの解析結果から予想はつくのだが、一般的な対称二端子対回路についてはどうなるかを証明する必要があった。著者はそれを自明なこととしているが、工学や技術の実務ではそれは許されても理数系から見るとHeavisideの演算子法となんら変わらない。 Maximaを使って全体の回路とその鏡像回路を縦続接続した伝送行列を計算させて固有ベクトルを求めれば元の単一の対称二端子対回路のそれと同じことが確認できる。コンピュータが利用できるとどうしても力づくで結果を求める安易なアプローチに頼ると智慧が得られないという恒例である。 DirichletはGaussのD.A.を常に携えて暇さえあれば新解釈を試みていたが、その口癖は「計算ではなく思考を」というものだった。Gaussは計算の達人だったので、D.A.の証明中には人知の限界に迫る量の数式が羅列してある部分もあり難解を極めた。Dicrichletは一方でGaussに最大の敬意を持つと同時に批判的精神も持ち合わせていた。これは高木貞治にもあてはまるが、彼は自身だけはその批判の対象外としていた。高木貞治はその著書「近世数学史談」でGuassの天才としての一面だけでなくその暗黒面の両面を指摘しているものの、自らの人生もいつのまにかGuassのそれと同化していった。数学者でこのことを指摘したのは谷山ー志村予想で知られる志村五郎氏唯一人である。 Dicrichletの「Notation(記号）ではなくnotion(概念）によって」の真言はRiemannにも血脈として受け継がれていった。それは近代数学の血脈と化したといっても過言ではない。半面で近代数学は抽象的になりすぎた感があり、現実問題とのつながりを極力もたないように説明されたり教えられたりする傾向にあることは否めない。数学は物理の世界に光りを点すと言われるように、今回の問題も線型代数的な視点でみると、闇に包まれた部分が著者の解答にいくつも残されていることを明るみにすることができた。同様にいくつか光があたったものの、その姿を正確に捉えることができないものがいくつか残されている。例えば、非対称回路の伝送行列の固有値と固有ベクトルがその鏡像回路と縦続接続してできる２組の対称回路の固有値と固有ベクトルとどういった関係があるのか。予想ではそれは複素共役と良く似た関係があるように思える。それぞれの和と差を計算してみると、何かの二倍となるとか、伝達定数（固有値）が二分割した回路のそれぞれの伝達係数の和に等しくなる点とか。また２組の対称回路の固有値は同じであることを自明として扱ってきたが、ちゃんと証明してはいない。少なくともこれらの疑問に明快に結論を出すには数学的な視点や考え方、論理が不可欠である。数学者になる必要はないが数学をお友だちにすることは非常に頼もしい。かつての日本は勤勉さを売りにしてきたが、同じ水準の勤勉さだったなら工数単価の安いアジアの中国やベトナム、韓国、北朝鮮に敵わないだろう。そう考えると日本の将来がどういった方向に向かうべきかは自ずと見えてくる。

« 1 2 (3) 4 5 6 7 »

スレッド表示 | 新しいものから

前のトピック | 次のトピック | トップ

投稿するにはまず登録を